LCA(最近公共祖先)
先有一棵树,选两个点向上爬相遇的第一个点就是这两个点的lca,如2是1和7的lca,1是6和5的lca。理解了吧。
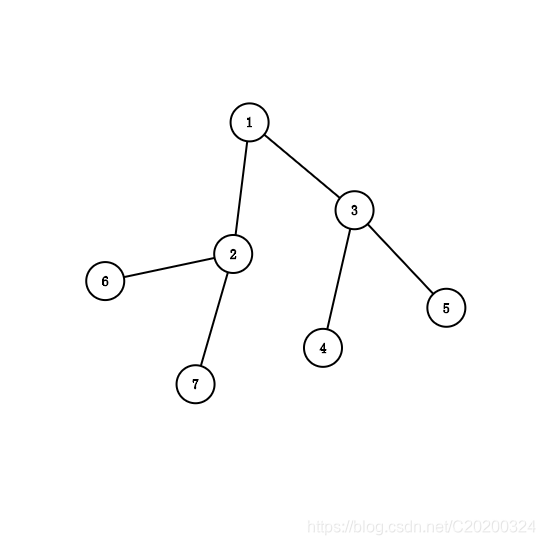
理解倒是很简单,现在来讲实现方法(四种)。
根据一道模板题来讲吧
一般的lca题都是求边权和,因为他们懒得给根为了让你随便选一个当根。
一.暴力搜索
两个先到同一深度,再一起向上爬,时间复杂度贼高(每次操作O(n)),但简单易懂。
见代码(我没打,借的同学的(@PI_RE-fsy))注:会超时,且不保证AC,重在理解。
#include <cstdio>
#include <vector>
using namespace std;
#define N 40000
#define reg register
inline void read (int &x){
x = 0;
char c = getchar ();
while (c < '0' || c > '9')
c = getchar ();
while (c >= '0' && c <= '9'){
x = (x << 1) + (x << 3) + c - 48;
c = getchar ();
}
}
inline void print (int x){
if (x / 10)
print (x / 10);
putchar (x % 10 + 48);
}
struct edge{
int v, w;
edge (){};
edge (int V, int W){
v = V;
w = W;
}
};
int n, m, k, fa[N + 5], dep[N + 5], dis[N + 5];
vector <edge> G[N + 5];
inline void dfs (int u, int f){//铺路,算出深度和权值(到根的距离)
for (reg int i = 0; i < G[u].size(); i++){
int v = G[u][i].v;
if (v == f) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
dis[v] = dis[u] + G[u][i].w;
dfs (v, u);
}
}
inline int LCA (int u, int v){
while (dep[u] > dep[v]) u = fa[u];//调整深度
while (dep[v] > dep[u]) v = fa[v];
if (u == v) return u;
while (u != v){//一起爬
u = fa[u];
v = fa[v];
}
return u;
}
int main (){
read (n); read (m);
for (reg int i = 1; i <= m; i++){
int u, v, w;
read (u); read (v); read (w);
G[u].push_back (edge (v, w));
G[v].push_back (edge (u, w));
}
fa[1] = 1, dep[1] = 0, dis[1] = 0;
dfs (1, 0);
read (k);
while (k --){
int u, v;
read (u); read (v);
int lca = LCA (u, v);
print (dis[u] + dis[v] - dis[lca] * 2);//类似于尺取法
putchar (10);
}
}二.dfs序(欧拉序)+rmq(区间维护最(大/小(该题用深度最浅))值)
普及一下dfs序:顾名思义,就是dfs的遍历顺序。(注:为满足求祖先,返回到某点,yeya也要记录一次,如开篇的那棵树的dfs序就是1262721343531。
而两点的lca就是这两点第一次出现在序列上所框出的这个区间中深度最小的点。这是可考证的,因为其中一点必须经过这个点才能搜到另一个点,所以就是LCA。
理解到这里,就更头痛le,因为rmq也有很多维护方法,列举两种(st表和线段树),复杂度自己取舍,一般差不多
线段树大家都会,如若不会,可查看我日后会写的小结复杂度(每次操作log(n))。
st表在这里说一下,是一种dp:dp(i,j)表示由i到i+2^(j)这段区间中最浅度(预处理nlogn,每次O(1))。
转换方程:dp(i,j)=max(dp(i,j-1),dp(i+pow(j-1),j-1));
见线段树代码
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define M 40050
inline void read(int &x) {
x = 0;
int f = 1;
char s = getchar();
while (s < '0' || s > '9') {
if (s == '-')
f = -1;
s = getchar();
}
while (s >= '0' && s<='9') {
x = x * 10 + s - '0';
s = getchar();
}
x *= f;
}
struct node {
int v,e;
node(int U,int E) {
v=U,e=E;
}
};
vector<node>G[M];
int n,m,dep[M],ver[M],que[M*2],tot,id[M],rmq[(M*2)<<2];
bool vis[M];
void built(int x,int deep) {
vis[x]=1;
que[++tot]=x;
id[x]=tot;
dep[x]=deep;
for(int i=0; i<G[x].size(); i++) {
if(!vis[G[x][i].v]) {
ver[G[x][i].v]=ver[x]+G[x][i].e;
built(G[x][i].v,deep+1);
que[++tot]=x;
}
}
return ;
}
void build(int k,int l,int r) {//建线段树
if(l==r) {
rmq[k]=que[l];
return ;
}
int mid=(l+r)/2;
build(k*2,l,mid);
build(k*2+1,mid+1,r);
if(dep[rmq[k*2]]<dep[rmq[k*2+1]])
rmq[k]=rmq[k*2];
else
rmq[k]=rmq[k*2+1];
}
int rmq1(int k,int l,int r,int a,int b) {//线段树查询
if(a<=l&&r<=b)
return rmq[k];
int u,v,mid=(l+r)/2;
u=v=0;
if(a<=mid)
v=rmq1(k*2,l,mid,a,b);
if(b>mid)
u=rmq1(k*2+1,mid+1,r,a,b);
if(dep[u]<dep[v])//比深度
return u;
else
return v;
}
int main() {
dep[0]=2147483647;
read(n),read(m);
for(int i=1; i<=m; i++) {
int x,y,e;
read(x),read(y),read(e);
G[x].push_back(node(y,e));
G[y].push_back(node(x,e));
}
built(1,1);
build(1,1,n*2-1);
int k;
read(k);
for(int i=1; i<=k; i++) {
int x,y;
read(x),read(y);
if(id[x]>id[y]) {//z注意!!!!!!!!!!!
swap(x,y);
}
printf("%d\n",ver[x]+ver[y]-ver[rmq1(1,1,tot,id[x],id[y])]*2);
}
}st表
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define M 40050
inline void read(int &x) {
x = 0;
int f = 1;
char s = getchar();
while (s < '0' || s > '9') {
if (s == '-')
f = -1;
s = getchar();
}
while (s >= '0' && s<='9') {
x = x * 10 + s - '0';
s = getchar();
}
x *= f;
}
struct node {
int v,e;
node(int U,int E) {
v=U,e=E;
}
};
vector<node>G[M];
int n,m,dep[M],ver[M],que[M*2],tot,id[M],dp[M*2][33],_pow[33];
bool vis[M];
void built(int x,int deep) {
vis[x]=1;
que[++tot]=x;
id[x]=tot;
dep[x]=deep;
for(int i=0; i<G[x].size(); i++) {
if(!vis[G[x][i].v]) {
ver[G[x][i].v]=ver[x]+G[x][i].e;
built(G[x][i].v,deep+1);
que[++tot]=x;
}
}
return ;
}
void build(int len) {
int K=(int)(log((double)len)/log(2.0));这段就是2的多少次方,可以直接复制。
_pow[0]=1;
for (int i=1; i<=len; i++){
dp[i][0]=que[i];
}
for(int i=1;i<=K;i++){//预处理的预处理,记住2的方
_pow[i]=_pow[i-1]*2;
}
for(int j=1;j<=K;j++){
for(int i=1;i+_pow[j]-1<=len;i++){
int a=dp[i][j-1],b=dp[i+_pow[j-1]][j-1];
if(dep[a]<dep[b])
dp[i][j]=a;
else
dp[i][j]=b;
}
}
return;
}
int rmq1(int a,int b) {
int K=(int)(log((double)b-a+1)/log(2.0));
int x=dp[a][K],y=dp[b-_pow[K]+1][K];
if(dep[x]<dep[y])//比较深度
return x;
return y;
}
int main() {
read(n),read(m);
for(int i=1; i<=m; i++) {
int x,y,e;
read(x),read(y),read(e);
G[x].push_back(node(y,e));
G[y].push_back(node(x,e));
}
built(1,1);
build(tot);
int k;
read(k);
for(int i=1; i<=k; i++) {
int x,y;
read(x),read(y);
if(id[x]>id[y]) {
swap(x,y);
}
printf("%d\n",ver[x]+ver[y]-ver[rmq1(id[x],id[y])]*2);
}
}三.倍增
同样是爬,这就更快了。2倍爬。
和st表求区间最值类似
•暴力求区间最值需要一个一个比较
•暴力求lca需要一步一步爬树
•st表用倍增比较一段和一段间的最值
•启发我们求lca也用倍增,一下向上爬2^i个点
•同样是在线算法
•设f(i,j)表示点i向上跳2^j步之后的点
•边界条件: f(i,0)表示向上跳一步的点,即fa(i)
•转移:要跳2^j步,先跳2^(j-1)步,再跳2^(j-1)步
•f(i,j)=f(f(i,j-1),j-1)(记住这个式子,同格式可以在倍增途中求最大边之类的东西)
•先调整u,v到同一深度(深的点向上爬)
•不过别一步一步爬,用f数组向上跳
•再让u,v一起向上跳
•从大到小枚举j,试图让u和v向上跳2^j步,如果u和v将要跳到同一个点,就不跳(因为可能跳到lca的上面),否则就爬树
•最后向上爬一步就是lca,时间复杂度O(logn)
上代码
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define M 40050
#define maxk 16
inline void read(int &x) {
x = 0;
int f = 1;
char s = getchar();
while (s < '0' || s > '9') {
if (s == '-')
f = -1;
s = getchar();
}
while (s >= '0' && s<='9') {
x = x * 10 + s - '0';
s = getchar();
}
x *= f;
}
struct node {
int v,e;
node(int U,int E) {
v=U,e=E;
}
};
vector<node>G[M];
int n,m,dep[M],ver[M],tot,f[M*2][33];
bool vis[M];
void build(int x,int deep) {
vis[x]=1;
dep[x]=deep;
for(int i=0; i<G[x].size(); i++) {
if(!vis[G[x][i].v]) {
ver[G[x][i].v]=ver[x]+G[x][i].e;
f[G[x][i].v][0]=x;
build(G[x][i].v,deep+1);
}
}
return ;
}
void built(){
build(1,1);
f[1][0]=1;
for(int j=1;j<=maxk;j++)
for(int i=1;i<=n;i++){
f[i][j]=f[f[i][j-1]][j-1];
}
}
void ad(int &u,int deep){
for(int i=maxk;i>=0;i--)
if(dep[f[u][i]]>=deep)
u=f[u][i];
}
int lca(int u,int v){
if(dep[u]>dep[v]){
ad(u,dep[v]);
}else if(dep[v]>dep[u]){
ad(v,dep[u]);
}
if(u==v)
return u;
for(int i=maxk;i>=0;i--){
if(f[u][i]!=f[v][i])
u=f[u][i],v=f[v][i];
}
return f[u][0];
}
int main() {
read(n),read(m);
for(int i=1; i<=m; i++) {
int x,y,e;
read(x),read(y),read(e);
G[x].push_back(node(y,e));
G[y].push_back(node(x,e));
}
built();
int k;
read(k);
for(int i=1; i<=k; i++) {
int x,y;
read(x),read(y);
int lca1=lca(x,y);
printf("%d\n",ver[x]+ver[y]-ver[lca1]*2);
}
}
四.tarjan(利用并查集求lca)
•离线算法
•先记录所有询问,然后对树做一次dfs求出所有点对的lca
•由dfs序可知,访问一个点是进入这个点,再退出的过程
•在进入u这个点的时候,把边(u,fa(u))删除,此时就形成以u为根的一棵子树,并且记录u已被访问过,然后依次遍历u的所有子节点
•在遍历结束后,查找所有跟u有关的查询(u,vi),若vi已被访问过,则lca(u,vi)是vi所在子树的根
•最后在退出u的时候把边(u,fa(u))重新加上
•假设1就是lca(2,3),且1不等于2或3
•那么2,3一定在 以1的两个不同的儿子为根的子树中
•现在先dfs到2,发现3还没访问过,不更新答案
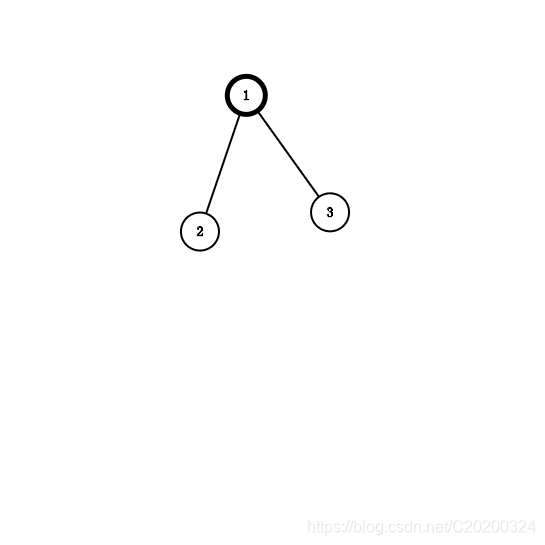
•假设u就是lca(u,v)
•现在先dfs到u,发现v还没访问过,不更新答案
•再dfs到v,发现u访问过了,u所在的子树的根是u,这样就求出了lca
算法实现
•实际上删边,加边和查询所在子树的根都不方便直接实现
•假设一开始边都是被删掉的(假设边被删掉了也可以走,只是对查询所在子树的根有影响),在退出的时候才把边加上
•现在只加边,且查询所在子树的根,可以用并查集实现
•在初始化或者进入u这个点的时候,让f(u)=u(这里的f是并查集中的,不是树上的)
•在退出u的时候,让f(u)=fa(u)
•查询u所在子树就变成find(u)
•设并查集时间复杂度为常数,则时间复杂度O(n+m)。
上代码
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define M 40050
#define maxk 16
inline void read(int &x) {
x = 0;
int f = 1;
char s = getchar();
while (s < '0' || s > '9') {
if (s == '-')
f = -1;
s = getchar();
}
while (s >= '0' && s<='9') {
x = x * 10 + s - '0';
s = getchar();
}
x *= f;
}
struct node {
int v,e;
node(int U,int E) {
v=U,e=E;
}
};
vector<node>G[M],Q[M];
int k,n,m,dep[M],ver[M],tot,f[M],ans[M/4];
bool vis[M];
void build(int x,int deep) {
vis[x]=1;
dep[x]=deep;
for(int i=0; i<G[x].size(); i++) {
if(!vis[G[x][i].v]) {
ver[G[x][i].v]=ver[x]+G[x][i].e;
build(G[x][i].v,deep+1);
}
}
return ;
}
void makeset(int x){
for(int i=1;i<=x;i++)
f[i]=i,vis[i]=0;
}
int findset(int x){
if(x!=f[x]){
f[x]=findset(f[x]);
}
return f[x];
}
void united(int x,int y){
int u=findset(x),v=findset(y);
f[v]=u;
return ;
}
void tarjan(int u){
vis[u]=1;
for(int i=0;i<G[u].size();i++){
if(!vis[G[u][i].v]){
tarjan(G[u][i].v);
united(u,G[u][i].v);
}
}
for(int i=0;i<Q[u].size();i++){
if(vis[Q[u][i].v])
ans[Q[u][i].e]=ver[u]+ver[Q[u][i].v]-ver[findset(Q[u][i].v)]*2;
}
}
int main() {
read(n),read(m);
for(int i=1; i<=m; i++) {
int x,y,e;
read(x),read(y),read(e);
G[x].push_back(node(y,e));
G[y].push_back(node(x,e));
}
build(1,1);
read(k);
for(int i=1; i<=k; i++) {
int x,y;
read(x),read(y);
Q[x].push_back(node(y,i));
Q[y].push_back(node(x,i));
}
makeset(n);
tarjan(1);
for(int i=1;i<=k;i++){
printf("%d\n",ans[i]);
}
}




















 9162
9162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








