数理统计三大分布：卡方分布、t分布、F分布

正态分布

由于${\chi }^2$（chi-squard）分布、t分布、F分布都是由正态分布构造的，首先对正态分布密度函数定义有

$$P(x)=\frac{1}{\sqrt{2\pi }\sigma }{\exp }^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

而标准化的正态分布为

$$P(x)=\frac{1}{\sqrt{2\pi }}{\exp }^{-\frac{x^2}{2}}$$

卡方分布

定义

设$X_1,X_2,......,X_n$相互独立并且都满足标准正态分布(0,1)，则称$r.v.$
$Y={\sum }_{i=1}^n{X}_i^2$ 服从自由度为$n$的${\chi }^2$分布，记为$Y\sim {\chi }^2(n)$

概率密度函数

$$f(x;n)=\frac{1}{2^{\frac{n}{2}}\Gamma (\frac{n}{2})}{x}^{\frac{n}{2}-1}{e}^{-\frac{x}{2}}（x>0）$$
其中$\Gamma (s)={\int }_0^{\infty }{e}^{-t}{t}^{s-1}dt(s>0)$，对于伽马函数$\Gamma (\cdot )$先挖个坑（可以暂时先看这个也挺不错的）。
对于不同参数的密度函数有：

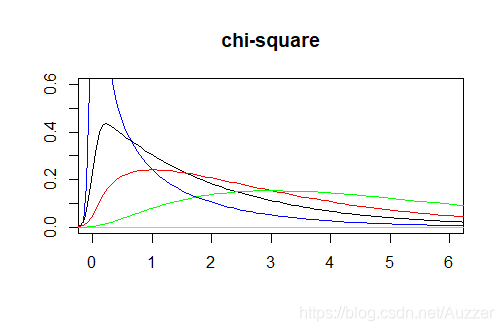
性质

t分布

定义

设$r.v.Z,Y$，其中$Z\sim N(0,1),X\sim {\chi }^2(n)$，则定义$r.v.T=\frac{Z}{\sqrt{X/n}}$为服从自由度为n的t分布。
对于不同参数的t分布密度函数有图如下：

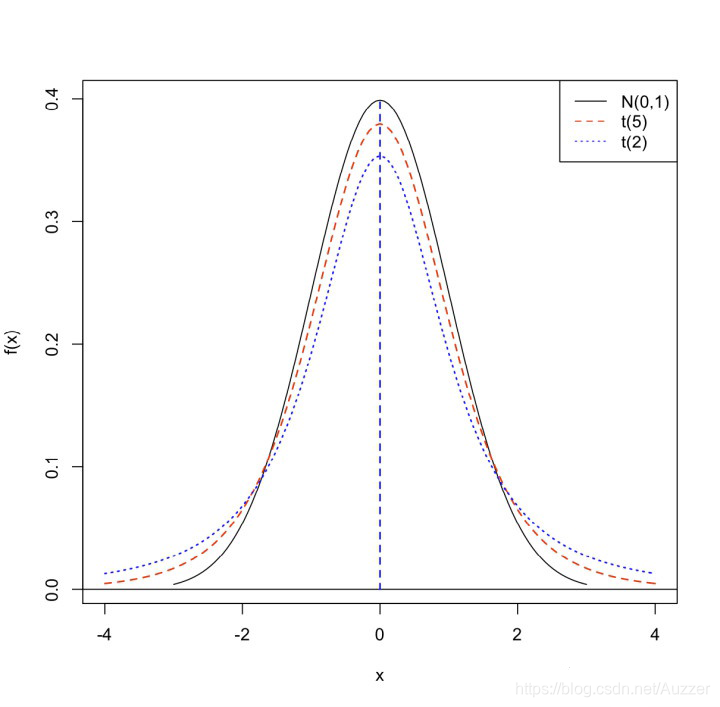
概率密度函数

性质

t分布主要是检验均值是否相同，在小样本中有着广泛的应用。同时t分布有着厚尾性质，对于一些性质不那么好的点比较宽容（比如t-SNE对于SNE的改进）。
特别值得注意的是，t(1)为Cauchy分布，就是那个令人讨厌的没有高阶矩的可恶的家伙，而当$n\to \infty$时候，t分布就趋向于正态分布。

F分布

定义

假设$r.v.X,Y$分别满足$X\sim {\chi }^2(n_1),Y\sim {\chi }^2(n_2)$，则称$r.v.Z=\frac{X/n_1}{Y/n_2}$为F分布

概率密度函数

对于不同参数的F分布密度函数有图如下：

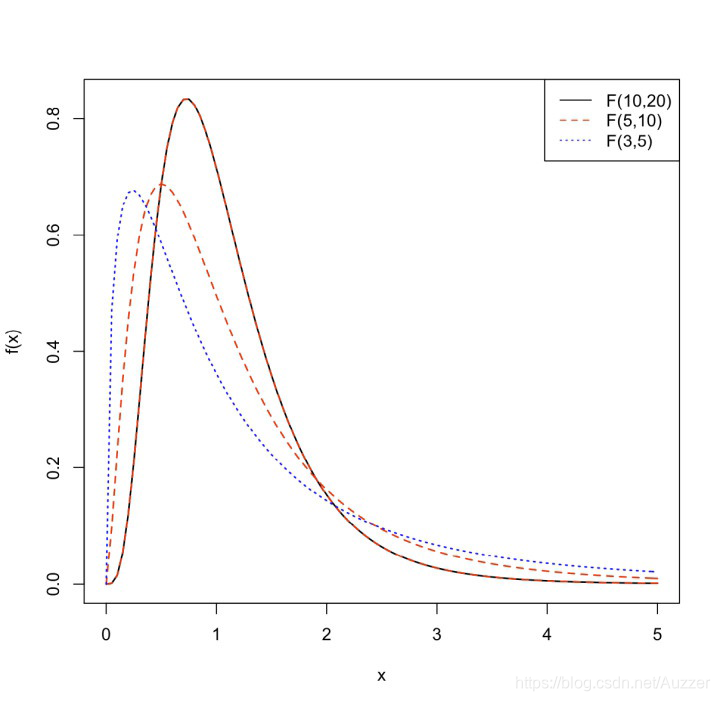
性质

我个人对F分布第一次有深刻印象是在方差检验中，现在回头来看F检验的定义，确定F检验是用来检验方差是否不同。

Attention

这三个分布是数理统计常用的分布，但特别要注意的是，t分布和F分布只能用来检验连续性数据，所以当检验数据特别稀疏的时候容易导致误判，而${\chi }^2$分布都可以。