POJ 3041 Asteroids

最新推荐文章于 2022-08-16 21:41:12 发布

AllBLue1117

最新推荐文章于 2022-08-16 21:41:12 发布

阅读量381

点赞数

CC 4.0 BY-SA版权

分类专栏：图论

本文链接：https://blog.youkuaiyun.com/Autii/article/details/52107416

图论专栏收录该内容

12 篇文章

订阅专栏


 
     
      Asteroids
     
     
      Time Limit: 1000MS   Memory Limit: 65536K
Total Submissions: 20318   Accepted: 11021
     
Description
     
      Bessie
 wants to navigate her spaceship through a dangerous asteroid field in the shape of an N x N grid (1 <= N <= 500). The grid contains K asteroids (1 <= K <= 10,000), which are conveniently located at the lattice points of the grid.  Fortunately, Bessie has a
 powerful weapon that can vaporize all the asteroids in any given row or column of the grid with a single shot.This weapon is quite expensive, so she wishes to use it sparingly.Given the location of all the asteroids in the field, find the minimum number of
 shots Bessie needs to fire to eliminate all of the asteroids.
     
Input
     
      * Line 1: Two integers
 N and K, separated by a single space.  * Lines 2..K+1: Each line contains two space-separated integers R and C (1 <= R, C <= N) denoting the row and column coordinates of an asteroid, respectively.
     
Output
     
      *
 Line 1: The integer representing the minimum number of times Bessie must shoot.
     
Sample Input
3 4
1 1
1 3
2 2
3 2
Sample
 Output
2
Hint
     
      INPUT
 DETAILS: 
      
The following diagram represents the data, where "X" is an asteroid and "." is empty space: 
      

      X.X 
.X. 
.X. 
      

      
OUTPUT DETAILS: 
      
Bessie may fire across row 1 to destroy the asteroids at (1,1) and (1,3), and then she may
 fire down column 2 to destroy the asteroids at (2,2) and (3,2).
     
Source
     
      USACO 2005 November Gold
     
[Submit]   [Go Back]   [Status]   [Discuss]
Home Page   Go Back  To top


 
	题目是ａ掉了，但是很多地方还是不大明白，关于二分图有太大的疑问，今天查了一晚的百度，终于有所收获。。 
	先是二分图的定义，二分图顾名思义也是图的一种，也就是离散上学的Ｇ（Ｓ，Ｖ）（Ｓ代表点集，Ｖ代表边集）的一种，二分图的定义则是：如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图： 
　　　　　　								 
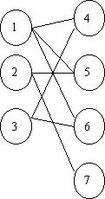
		然后是最大匹配的定义，匹配的意思是任意两条边都不依附于一个定点的边集，如上图中边集｛（１，５），（２，７）｝是一个匹配，而｛（１，５），（２，７），（２．５）｝则不是，上图的最大匹配之一可为为｛（１，５），（２，７），（３，４）｝． 
		 
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int n, k;
bool map[500+5][500+5], vis[10000+5];
int match[500+5];
bool find(int x) {
    for(int i=1;i<=n;i++) {
        if(map[x][i]&&!vis[i]) {
            vis[i]=1;
            if(match[i]==0||find(match[i])) {
                match[i]=x;
                return true;
            }
        }
    }
    return false;
}
int main()
{
    scanf("%d %d", &n, &k);
    memset(map,0,sizeof(map));
    memset(match,0,sizeof(match));
    for(int i=1;i<=k;i++) {
        int x, y;
        scanf("%d %d", &x, &y);
        map[x][y]=1;
    }
    int ans=0;
    for(int i=1;i<=n;i++) {
        memset(vis,0,sizeof(vis));
        if(find(i)) ans++;
    }
    printf("%d\n", ans);
    return 0;
}