【CV】常用的损失函数

1. 前言

在总结常用的损失函数之前，我们来先回顾一下损失函数（Loss Function）、代价函数（Cost Function）和目标函数（Objective Function）的区别和联系。
在机器学习的语境下，这三个术语经常被交叉使用。

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型性能越好。不同模型用的损失函数一般也不一样。

损失函数分为经验风险损失函数和结构风险损失函数。
经验风险损失函数指 预测结果和实际结果的差别，
结构风险损失函数指 经验风险损失函数+正则项。

1.1. 区别

1. 损失函数（Loss Function）通常是针对单个训练样本而言，给定一个模型 f 输出值y^i和一个真实值yi,损失函数输出一个实值损失：

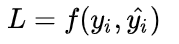
2. 代价函数（Cost Function）通常是针对整个训练集（或者在使用mini-batch gradient descent时一个mini-batch）的总损失：

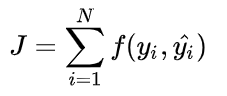
3. 目标函数（Objective Function）是一个更通用的术语，表示任意希望被优化的函数，用于机器学习领域和非机器学习领域（例如，运筹优化）

1.2. 联系

我们用一句话总结三者之间的关系就是：
A loss function is a part of a cost function which is a type of an objective function.

损失函数和代价函数只是在针对样本集上有区别，在论文和一些博客上都混着使用，但相关公式实际上是代价函数（Cost Function）的形式，这需要我们注意。

2. 常用损失函数

2.1. 0-1损失函数（zero-one loss）

0-1损失是指预测值和真实值不相等时为1，否则为0；
损失函数如下：

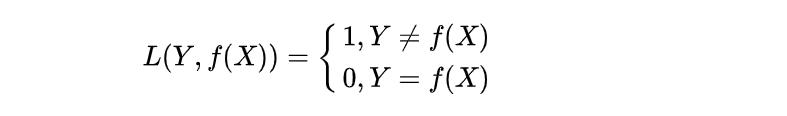
特点：
（1）0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用。
（2）感知机就是用的这种损失函数。但是，相等这个条件太过严格，因此可以放宽条件，即满足|Y-f(x)|<T时认为相等，此时函数关系式为：

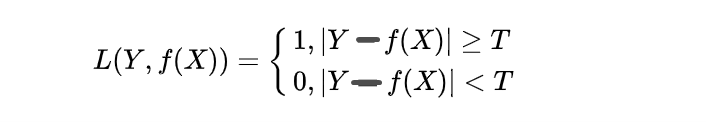
2.2. 均方差损失（Mean Squared Error Loss，MSE）

均方差 Mean Squared Error (MSE) 损失是机器学习、深度学习回归任务中最常用的一种损失函数，也称为 L2 Loss。函数形式如下：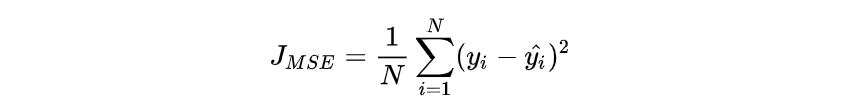
我们有时候也会称之为平方差损失函数。

从直觉上理解均方差损失，这个损失函数的最小值为 0（当预测等于真实值时），最大值为无穷大。
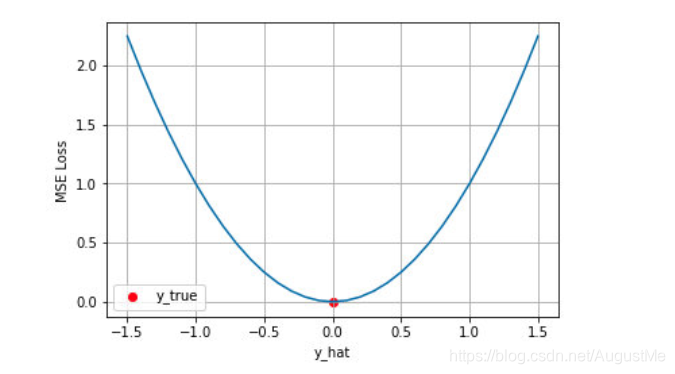
下图是对于真实值 y=0，不同的预测值 [-1.5,1.5] 的均方差损失的变化图。横轴是不同的预测值，纵轴是均方差损失，可以看到随着预测与真实值绝对误差 |y-y^|的增加，均方差损失呈二次方地增加。

2.3. 平均绝对差损失（Mean Absolute Error Loss，MAE）

平均绝对误差 Mean Absolute Error (MAE) 也称为L1 Loss。其基本形式如下：

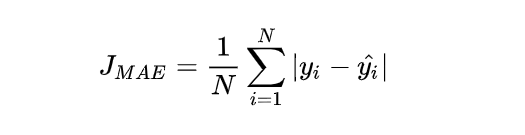
同样的我们可以对这个损失函数进行可视化如下图，MAE 损失的最小值为 0（当预测等于真实值时），最大值为无穷大。可以看到随着预测与真实值绝对误差|y-y^|的增加，MAE 损失呈线性增长。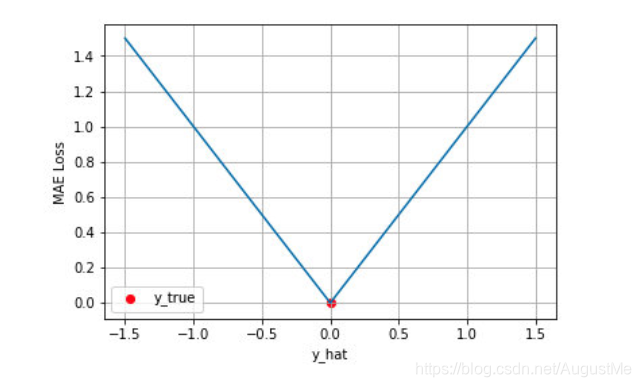
附加：MSE和MAE之间的区别
MSE（平均绝对值损失函数）和MAE（均方差损失函数）作为损失函数的主要区别：
1）MSE损失相比MAE，MSE通常可以更快地收敛，
2）MAE损失相比MSE，MAE对于outlier（离群点、异常点）更加鲁棒，即MAE不易受到outlier的影响。

下面进行分析：
MSE 通常比 MAE 可以更快地收敛。
当使用梯度下降算法时，MSE损失的梯度是变化的，而MAE损失的梯度是保持不变的，梯度不发生改变不利于模型的训练（当然可以使用动态调整学习率的方式缓解这个问题），但是总的来说，损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因。

MAE 对于 outlier 更加 robust

1. 第一个角度是直观地理解，下图是 MAE 和 MSE 损失画到同一张图里面，由于MAE 损失与绝对误差之间是线性关系，MSE 损失与误差是平方关系，当误差非常大的时候，MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的 outlier 时，MSE 会产生一个非常大的损失，对模型的训练会产生较大的影响。
   

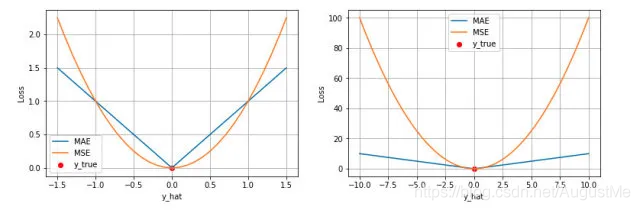
2. 第二个角度是从两个损失函数的假设出发，MSE 假设了误差服从高斯分布，MAE 假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于 outlier 更加 robust。参考下图（来源：Machine Learning: A Probabilistic Perspective 2.4.3 The Laplace distribution Figure 2.8），当右图右侧出现了 outliers 时，拉普拉斯分布相比高斯分布受到的影响要小很多。因此以拉普拉斯分布为假设的 MAE 对 outlier 比高斯分布为假设的 MSE 更加 robust。
   
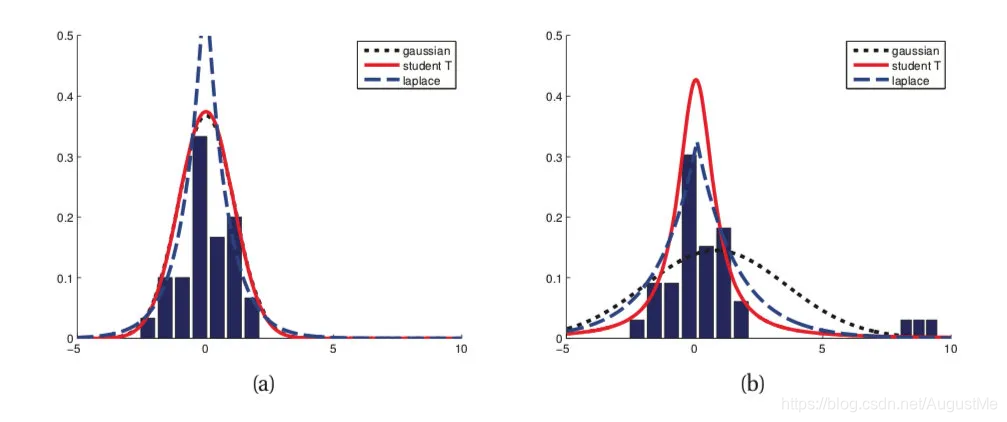
   注：高斯分布（也称为，正态分布，）均值μ=0、标准差σ=1
   
   拉普拉斯分布，μ 是位置参数，λ 是尺度参数。

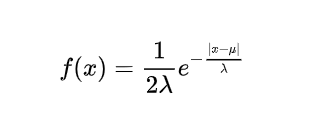
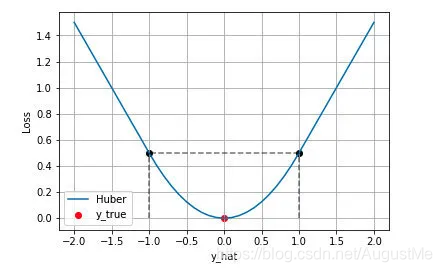
2.4. Huber Loss

上面我们分别介绍了 MSE 和 MAE 损失以及各自的优缺点，MSE 损失收敛快，但容易受 outlier 影响，MAE 对 outlier 更加健壮但是收敛慢，Huber Loss 则是一种将 MSE 与 MAE 结合起来，取两者优点的损失函数，也被称作 Smooth Mean Absolute Error Loss 。其原理很简单，就是在误差接近 0 时使用 MSE，误差较大时使用 MAE，公式为：

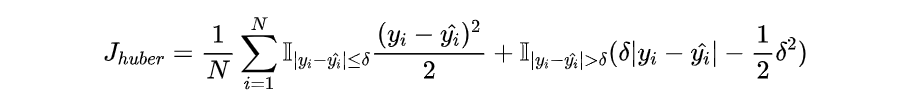
2.5. 分位数损失 Quantile Loss

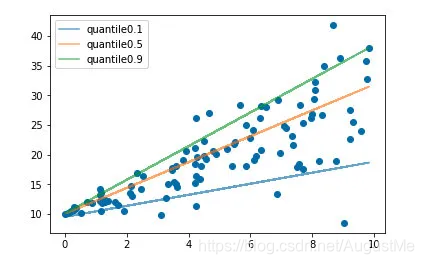
分位数回归 Quantile Regression 是一类在实际应用中非常有用的回归算法，通常的回归算法是拟合目标值的期望或者中位数，而分位数回归可以通过给定不同的分位点，拟合目标值的不同分位数。例如我们可以分别拟合出多个分位点，得到一个置信区间，如下图所示：

分位数回归是通过使用分位数损失 Quantile Loss 来实现这一点的，分位数损失形式如下，式中的 r 分位数系数。

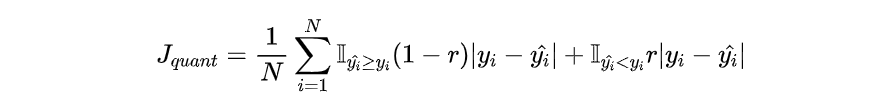
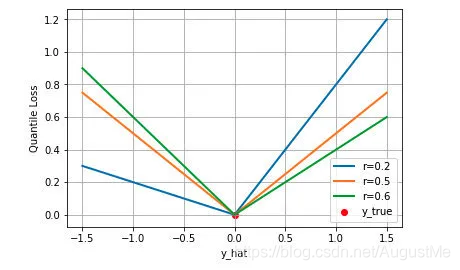
下图是取不同的分位点 0.2、0.5、0.6 得到的三个不同的分位损失函数的可视化，可以看到 0.2 和 0.6 在高估和低估两种情况下损失是不同的，而 0.5 实际上就是 MAE。

2.6. 交叉熵损失（Cross Entropy Loss）

2.6.1. 二分类

在二分类中，我们通常使用sigmoid函数将模型的输出压缩到（0,1）区间内，因此可以用来代表给定输入x_i，模型判断为正类的概率 p(x_i)。
负类的概率值为1 - p(x_i)
正类：p(y_i = 1 | x_i) = y^_i
负类：p(y_i = 0 | x_i) = 1 - y^_i
将上述两个式子进行合并：
y_i 只有两个取值，0或者1

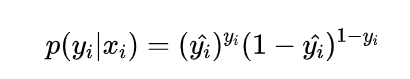
假设数据点之间独立同分布，则似然可以表示为：

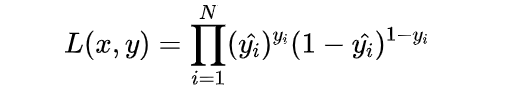
对似然取对数，然后加负号变成最小化负对数似然，即为交叉熵损失函数的形式

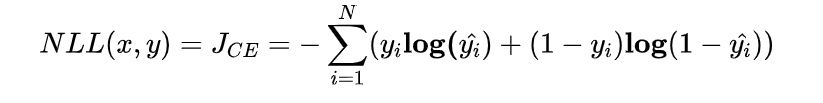
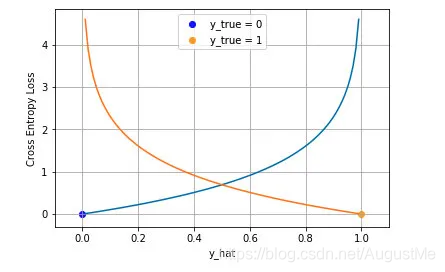
下图是对二分类的交叉熵损失函数的可视化，蓝线是目标值为 0 时输出不同输出的损失，黄线是目标值为 1 时的损失。可以看到约接近目标值损失越小，随着误差变差，损失呈指数增长。

2.6.2. 多分类

在多分类的任务中，交叉熵损失函数的推导思路和二分类是一样的，变化的地方是真实值y_i现在是一个 One-hot 向量，同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在（0,1）之间，同时所有维度的输出和为 1，用于表示一个概率分布。

思考：为什么交叉熵损失比较好，分类中为什么不用均方差损失？

分类中为什么不用均方差损失？上文在介绍均方差损失的时候讲到实际上均方差损失假设了误差服从高斯分布，在分类任务下这个假设没办法被满足，因此效果会很差。
为什么是交叉熵损失呢？有两个角度可以解释这个事情，一个角度从最大似然的角度，也就是我们上面的推导；另一个角度是可以用信息论来解释交叉熵损失：

2.7. 合页损失（Hinge Loss）

合页损失 Hinge Loss 是另外一种二分类损失函数，适用于 maximum-margin 的分类，支持向量机 Support Vector Machine (SVM) 模型的损失函数本质上就是 Hinge Loss + L2 正则化。合页损失的公式如下

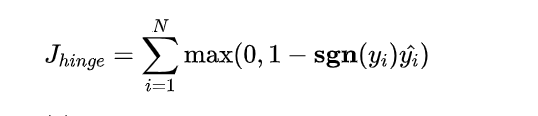
f(x) = sgn(x)
当x>0, f(x) = 1
当x=0, f(x) = 0
当x<0, f(x) = -1

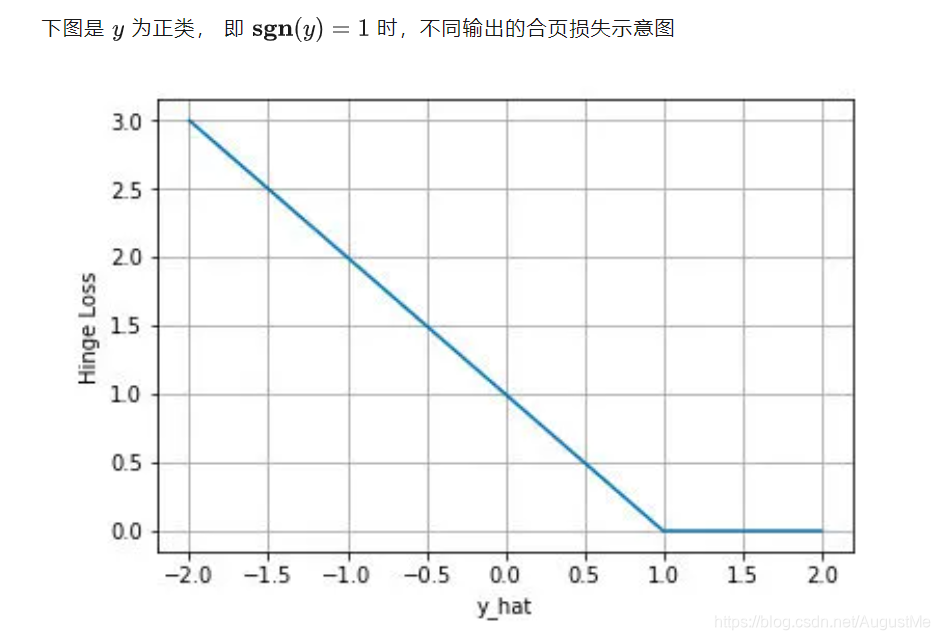
可以看到当y为正类时，模型输出负值会有较大的惩罚，当模型输出为正值且在(0,1)区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的，并且对于预测对了但是置信度不高的也会给一个惩罚，只有置信度高的才会有零损失。使用合页损失直觉上理解是要找到一个决策边界，使得所有数据点被这个边界正确地、高置信地被分类。

3.总结

本文针对机器学习中最常用的几种损失函数进行相关介绍，首先是适用于回归的均方差损失（Mean Squared Error Loss，MSE） 、平均绝对误差损失 （Mean Absolute Error Loss，MAE），两者的区别以及两者相结合得到的 Huber Loss，接着是应用于分位数回归的分位数损失 Quantile Loss，表明了平均绝对误差损失实际上是分位数损失的一种特例；
在分类场景下，本文讨论了最常用的交叉熵损失函数 Cross Entropy Loss，包括二分类和多分类下的形式，并从信息论的角度解释了交叉熵损失函数，最后简单介绍了应用于 SVM 中的 Hinge 损失 Hinge Loss。

本文还有其他许多损失函数没有提及，比如应用于 Adaboost 模型中的指数损失 Exponential Loss，Smooth L1 Loss，对数损失。另外通常在损失函数中还会有正则项（L1/L2 正则），这些正则项作为损失函数的一部分，通过约束参数的绝对值大小以及增加参数稀疏性来降低模型的复杂度，防止模型过拟合，这部分内容在本文中也没有详细展开，需要我们继续查阅资料进行学习。

4.参考（References）

https://blog.youkuaiyun.com/lyl771857509/article/details/79428475

https://zhuanlan.zhihu.com/p/77686118

https://mp.weixin.qq.com/s/nsnc6RAzByzDuUyYNNOKDA

https://zhuanlan.zhihu.com/p/58883095