深度学习入门2—— 神经网络的组成和3层神经网络的实现

由上一章结尾，我们知道神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。接下来会介绍神经网络的概要，然后再结合手写数字识别案例进行介绍。

1.神经网络概要

1.1从感知机到神经网

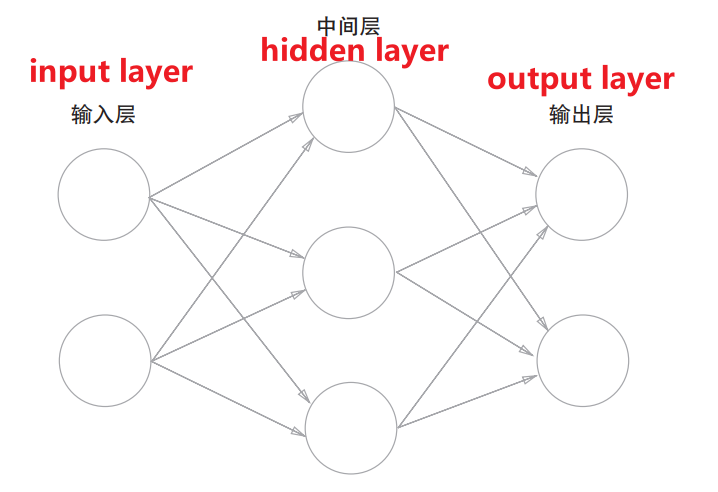
我们可以用图来表示神经网络，我们把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层（隐藏层）。

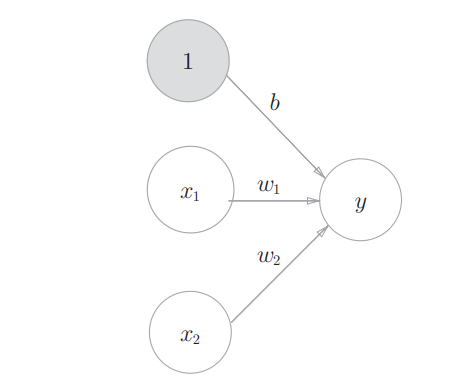
在感知机的基础上，我们添加权重为b的输入信号1。这个感知机将x1、x2、1三个信号作为神经元的输入，将其和各自的权重相乘后传送至下一个神经元。在下一个神经元中，计算这些加权信号的总和。由于偏置的输入信号一直是1， 所以为了区别于其他神经元，我们在图中把这个神经元整个涂成灰色（如下图所示）。

我们改写感知机的数学表达式，用一个函数h(x)来表示这种分情况的动作（超过0则输出1，否则输出0）：

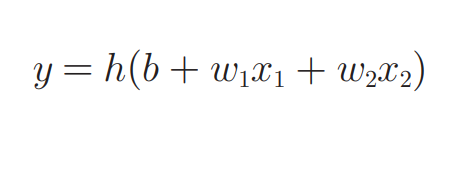
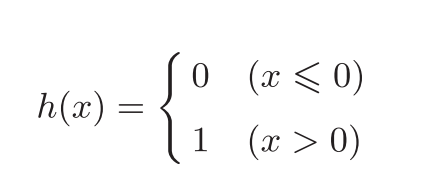
1.2激活函数（连接感知机和神经网络的桥梁。）

先来了解一下神经网络中的激活函数的概念。上面给出的h（x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。如“激活”一词所示，__激活函数的作用在于决定如何来激活输入信号的总和。__神经网络可表达为如下方式：

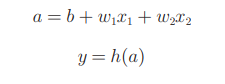
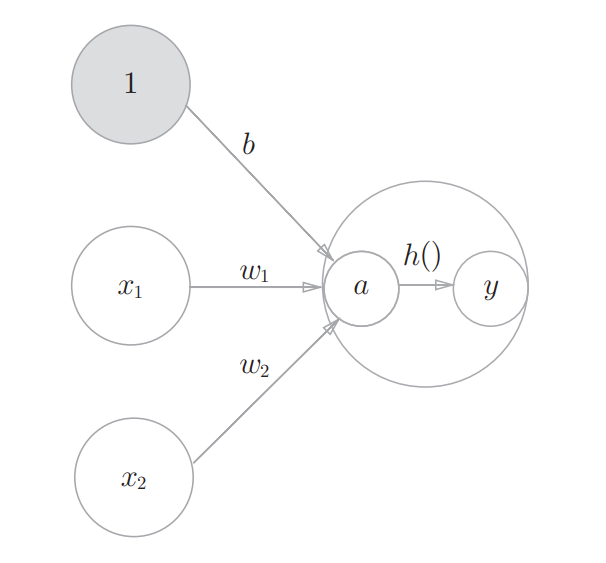
上述图像展示了信号的加权总和为节点a被激活函数h()转换成节点y的详细过程。在一般的神经网络图中不表达为上述形式，而是以一个圆圈表示上述的整个过程。

接下来介绍几种常用的激活函数：

① sigmoid函数（水车，根据流入量决定流出量）

exp（-x）指的是e （−x）次方 ，e为的自然常数（纳皮尔常数2.7182…）。其本质就是给定某个输入后，会返回某个输出的转换器。值得注意的是，sigmoid函数的平滑性对神经网络的学习具有重要意义。sigmoid函数的图像及代码实现如下所示。

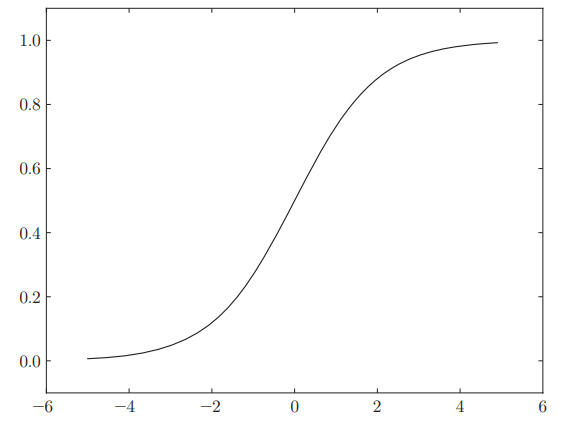
    def sigmoid(x):
        return 1 / (1 + np.exp(-x))

② 阶跃函数（竹筒敲石，到达一定值才输出1）