例题解析——有线电视网

原创已于 2025-12-18 20:22:18 修改 · 482 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #动态规划 #深度优先 #树

于 2025-12-17 20:45:04 首次发布

一、题面

https://www.luogu.com.cn/problem/P1273https://www.luogu.com.cn/problem/P1273

1.题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

2.输入格式

第一行：两个用空格隔开的整数 N 和 M，其中 2≤N≤3000，1≤M≤N−1，N 为整个有线电视网的结点总数，M 为用户终端的数量。

P.S.第一个转播站即树的根结点编号为 1，其他的转播站编号为 2 到 N−M，用户终端编号为 N−M+1 到 N。

接下来的 N−M 行：每行表示—个转播站的数据，第 i+1 行表示第 i 个转播站的数据，其格式如下：K A1 C1 A2 C2 … Ak Ck

K 表示该转播站下接 K 个结点（转播站或用户），每个结点对应一对整数 A 与 C ，A 表示结点编号，C 表示从当前转播站传输信号到结点 A 的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。单次传输成本和用户愿意交的费用均不超过 10。

3.输出格式

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

4.输入输出样例

输入

输出

5.样例解释

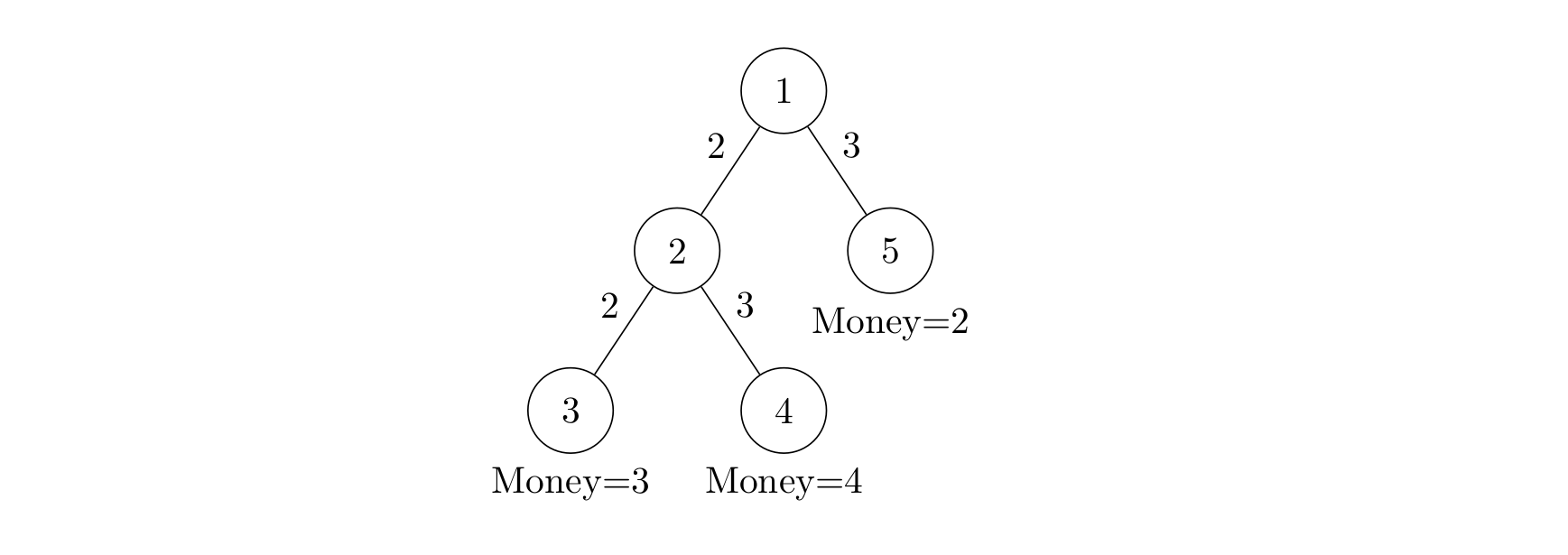
如图所示，共有五个结点。结点 ① 为根结点，即现场直播站，② 为一个中转站，③④⑤ 为用户端，共 M 个，编号从 N−M+1 到 N，他们为观看比赛分别准备的钱数为 3、4、2。

从结点 ① 可以传送信号到结点 ②，费用为 2；

也可以传送信号到结点 ⑤，费用为 3（第二行数据所示）；

从结点 ② 可以传输信号到结点 ③，费用为2；

也可传输信号到结点 ④，费用为 3（第三行数据所示）。

如果要让所有用户（③④⑤）都能看上比赛，则信号传输的总费用为：2+3+2+3=10，大于用户愿意支付的总费用 3+4+2=9，有线电视网就亏本了，而只让 ③④ 两个用户看比赛就不亏本了。

二、主体思路

这道题考察了树、DFS和DP背包合并的知识点，主体思路为用DFS遍历信号传输树，用背包合并把子节点的答案合并到父节点上来。最后复杂度会收敛至O(m²)，能过。关注我的话，可以看到下一篇例题解析和这道题思路较为相似。

三、代码“碎片”&分布解析

1.全局定义等

#include <bits/stdc++.h>
using namespace std;
#define N 3000
#define M 3000
#define INF 40000
#define int long long

struct node
{
	int y,c;//  cost
};
int rs;//relay station
vector<node>adj[N+10];//adj[x]:结点x的所有孩子
int dp[N+10][M+10];//dp[x][i]:在以x为根的子树中服务i个用户的最大利润 
int k[N+10],mny[N+10],cn[N+10];//  money  client number cn[x]:在以x为根的子树中用户数

INF可以推算出，应>30000。

2.主函数

signed main()
{

由于全局定义时有#define int long long，这里要写signed main而非int main（否则见祖宗...(*￣０￣)ノ）

(1)输入

	int n,m;
	cin>>n>>m;
	rs=n-m;
	for(int i=1;i<=rs;i++)
	{
		cin>>k[i];
		for(int j=1;j<=k[i];j++)
		{
			int a,c;//  cost
			cin>>a>>c;
			adj[i].push_back({a,c});
		}
	}
	for(int i=1;i<=m;i++)
		cin>>mny[rs+i];

没什么要点，注意格式即可。

(2)初始化

	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			dp[i][j]=-INF;

把在以i为根的子树中，服务j个用户的最大利润设为负无穷（用于判断是否可能发生这种情况），只服务0个用户的话一定就是0。

(3)DFS&找到答案

	dfs(1);
	for(int i=m;i>=0;i--)
		if(dp[1][i]>=0)
		{
			cout<<i;
			
			return 0;
		} 
		
	return 0;
}

服务客户数从多到少遍历dp数组，如果服务i个用户没亏，就服务i个用户。

2.DFS函数

(1)用户结点情况

void dfs(int x)
{
	if(x>rs)
	{
		cn[x]=1;
		dp[x][1]=mny[x];
		
		return;
	}

rs就是转播站数量，所以>rs就是非用户结点。这样的话，在以x为根的子树中就是有它自己这一个用户，转播站服务用户x所得到的利润就是它所交的钱mny[x]。

(2)转播站节点情况——DP背包合并

	cn[x]=0;
	for(auto e:adj[x])
	{
		int &y=e.y,&c=e.c;//  cost
		dfs(y);
		for(int i=cn[x];i>=0;i--)
			for(int j=0;j<=cn[y];j++)
				if(dp[x][i]!=INF&&dp[y][j]!=INF)
					dp[x][i+j]=max(dp[x][i+j],dp[x][i]+dp[y][j]-c);
		cn[x]+=cn[y];
	}
}

初始时在以x为根的子树中一个用户也没有找到……

遍历每一个结点x的孩子——结点y，执行dfs(y)，即填充完结点y的信息后把y的背包合并到x的里。

再遍历i，也就是x自己不加y服务的用户数，注意要倒着来，如果正着来的话，现在把包含y的结果存进dp，i++后可能会叠加计算y的数据！

再再遍历j，也就是y要服务的用户数。如果结点x能服务i个结点，且结点y能服务j个结点，那么就把y的结果合并到x里。

吃合并完一个孩子后，把它的用户（数）也“吞并”就好啦（好坑娃）

四、完整代码

#include <bits/stdc++.h>
using namespace std;
#define N 3000
#define M 3000
#define INF 40000
#define int long long

struct node
{
	int y,c;//  cost
};
int rs;//relay station
vector<node>adj[N+10];
int dp[N+10][M+10];//dp[i][j]:在以i为根的子树中，服务j个用户的最大利润 
int k[N+10],mny[N+10],cn[N+10];//  money  client number
void dfs(int x)
{
	if(x>rs)
	{
		cn[x]=1;
		dp[x][1]=mny[x];
		
		return;
	}
	cn[x]=0;
	for(auto e:adj[x])
	{
		int &y=e.y,&c=e.c;//  cost
		dfs(y);
		for(int i=cn[x];i>=0;i--)
			for(int j=0;j<=cn[y];j++)
				if(dp[x][i]!=INF&&dp[y][j]!=INF)
					dp[x][i+j]=max(dp[x][i+j],dp[x][i]+dp[y][j]-c);
		cn[x]+=cn[y];
	}
}
signed main()
{
	int n,m;
	cin>>n>>m;
	rs=n-m;
	for(int i=1;i<=rs;i++)
	{
		cin>>k[i];
		for(int j=1;j<=k[i];j++)
		{
			int a,c;//  cost
			cin>>a>>c;
			adj[i].push_back({a,c});
		}
	}
	for(int i=1;i<=m;i++)
		cin>>mny[rs+i];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			dp[i][j]=-INF;
	dfs(1);
	for(int i=m;i>=0;i--)
		if(dp[1][i]>=0)
		{
			cout<<i;
			
			return 0;
		} 
		
	return 0;
}