线段树-基础-优快云博客

近14个月没写博客了！！！I’m back againヾ(≧▽≦*)o

一、认识

线段树是一种用结构体数组存储的二叉搜索树，用了分治思想，能把时间复杂度进行“降维打击”，实现对区间的O(logn)修改和查询总和，树状形态如下图。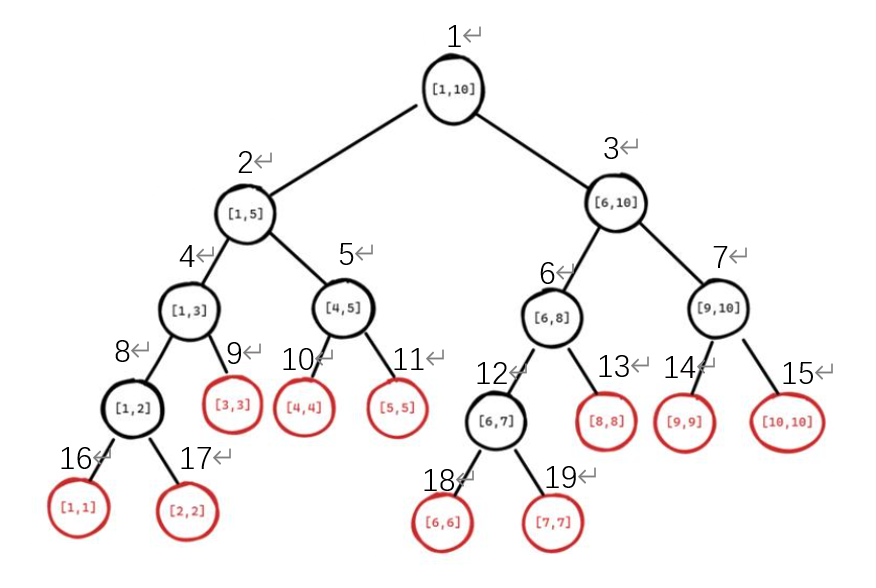

每一个结点（结构体t[i]，i是图中标注在圆圈上的下标）都包含了这些信息一个区间（即l和r）、一个和值s（即 $\sum_{i=l}^r a[i]$ ）和一个懒惰标记lzy（后续会讲）。可以发现，每一个非叶节点都被拆成了两部分，区间对应[l,mid]和[mid+1,r]，mid可取(l+r)/2，也可取图中的(l+r+1)/2（反正一定不要不要不要让两个区间重叠！！！）。

在用结构体数组存储时，根结点对应区间是[1,n]，下标为1；每个叶节点的l和r都相等，对应原数组。每个能“劈”成两半的结点如果下标为i，那么它的两个孩子的下标就分别为i*2和i*2+1。

二、代码&功能

1.存储&建树函数——build tree函数

得到n和a[]数组后，就可以执行build tree函数了。该函数是void类型，包括3个参数——结点下标i、a[]数组下标l和r（用来框出i结点对应的区间），用来给t[]这个结构体数组赋值（t[i].lzy——懒惰标记——初始时默认为0）。

先把t[i]的l和r赋值为参数中的l和r，再判断l和r是否相等：相等的话说明这是个叶结点，把t[i].s赋值为a[l]（或a[r]）即可；不相等的话说明可以分治，即递归求出给两个孩子赋值，算完再把它们的s加起来就好了。代码如下：

void bt(int i,int l,int r)//build tree
{
	node &nd=t[i];//node
	nd.l=l;
	nd.r=r;
	if(l==r)
		nd.s=a[l];
	else
	{
		int m=(l+r)/2;//middle
		bt(lc,l,m);
		bt(rc,m+1,r);
		nd.s=t[lc].s+t[rc].s;
	}
}

2.区间更新数值函数——update函数

当我们需要将区间[l,r]中的每个数都加上x时，如果用数组只能一个一个加，但用线段树只需要log级别的时间复杂度。update函数是void类型，包括4个参数——结点下标i、a[]数组下标l和r（就是输入进来的l和r，恒定不变，也可以定义在最外面）、和要增加的数x。

首先putdown(i)——在后面会讲到它的用途。随后判断t[i]是否有在[l,r]之间的部分，也就是与t[i]是否有一丝丝关系：如果没有直接return；如果t[i]被全部涵盖在了[l,r]内，说明整个t[i]所涵盖的部分全都要加x，这时就把它的s加上x*它所管理的数量，然后把它的lzy赋值为x——注意这里本来应该再递归，把它的后代全部都加上x*它们所管理的数量的，一会儿会说到；如果是部分包含，那么分别查看t[i]的两个孩子是否与[l,r]“沾边”，有的话就递归，最后还是再把它们的s加起来就好了。代码如下：

void ud(int i,int l,int r,int x)//update
{
	pd(i);
	node &nd=t[i];//node
	if(nd.r<l||nd.l>r)//完全不包含 
		return;
	
	if(nd.l>=l&&nd.r<=r)//完全包含 
	{
		nd.s+=x*(nd.r-nd.l+1);
		nd.lzy=x;
	}
	else//部分包含 
	{
		int m=(nd.l+nd.r)/2;//middle
		if(m>=l)
			ud(lc,l,r,x);
		if(m+1<=r)
			ud(rc,l,r,x);
		nd.s=t[lc].s+t[rc].s;
	}
}

3.区间求和函数——get sum函数

仍只需要log级别的时间复杂度！get sum函数是int（或long long、double等）类型，包括3个参数——结点下标i、a[]数组下标l和r（还是输入进来的l和r，恒定不变，也可以定义在最外面）。

首先putdown(i)——依旧在后面会讲到它的用途。随后判断t[i]是否有在[l,r]之间的部分：如果没有直接return 0；如果t[i]被全部涵盖在了[l,r]内，说明整个t[i]所涵盖的部分全都都被算上了，return它的s；如果是部分包含，那么分别查看t[i]的两个孩子是否有在[l,r]之间的部分，有的话就递归算，最后仍是再把它们的结果加起来return。代码如下：

int gs(int i,int l,int r)//get sum
{
	pd(i);
	node &nd=t[i];//node
	if(nd.r<l||nd.l>r)//完全不包含 
		return 0;
	
	if(nd.l>=l&&nd.r<=r)//完全包含 
		return nd.s;
		
	else//部分包含 
	{
		int ans=0;
		int m=(nd.l+nd.r)/2;
		if(m>=l)
			ans+=gs(lc,l,r);
		if(m+1<=r)
			ans+=gs(rc,l,r);
		
		return ans;
	}
}

4.“清理债务”函数——pushdown函数

终于到了揭晓谜底的时候了q(≧▽≦q)！先说pushdown函数关系极大的懒惰标记lazy，在update函数中它被赋值为了x，而t[i]就没有让它的后代都加上相应倍的x，而pushdown函数就是在做这件事。把处理后代的“债务”拖到必要时再做，一定程度上降低了时间复杂度。pushdown函数只包括一个参数——结点下标i。

在pushdown函数内部，先判断t[i]是否有lazy债——没有就不用操作了。随后把它的两个孩子的s都分别加上t[i]的债*它们自己所管理的数量，并且把孩子们们的lazy债都分别加上t[i]的债，再把自己的lazy债“清空”。这样做听起来有点坑娃……不过自己的娃会把债再传给孙子代的ㄟ( ▔, ▔ )ㄏ

三、洛谷模板完整代码

#include <bits/stdc++.h>
using namespace std;
#define N 100000
#define int long long
#define lc i*2//left child
#define rc i*2+1//right child

struct node
{
	int l,r,s,lzy;//lazy
}t[N*8+10];
int a[N+10];
void bt(int i,int l,int r)//build tree
{
	node &nd=t[i];//node
	nd.l=l;
	nd.r=r;
	if(l==r)
		nd.s=a[l];
	else
	{
		int m=(l+r)/2;//middle
		bt(lc,l,m);
		bt(rc,m+1,r);
		nd.s=t[lc].s+t[rc].s;
	}
}
void pd(int i)//pushdown
{
	node &nd=t[i];//node
	int &l=nd.lzy;//t[i]'s lazy
	if(l!=0)
	{
		node &ln=t[lc],&rn=t[rc];//left child's node  right child's node
		ln.s+=l*(ln.r-ln.l+1);
		ln.lzy+=l;
		rn.s+=l*(rn.r-rn.l+1);
		rn.lzy+=l;
		l=0;
	}
}
void ud(int i,int l,int r,int x)//update
{
	pd(i);
	node &nd=t[i];//node
	if(nd.r<l||nd.l>r)//完全不包含 
		return;
	
	if(nd.l>=l&&nd.r<=r)//完全包含 
	{
		nd.s+=x*(nd.r-nd.l+1);
		nd.lzy=x;
	}
	else//部分包含 
	{
		int m=(nd.l+nd.r)/2;//middle
		if(m>=l)
			ud(lc,l,r,x);
		if(m+1<=r)
			ud(rc,l,r,x);
		nd.s=t[lc].s+t[rc].s;
	}
}
int gs(int i,int l,int r)//get sum
{
	pd(i);
	node &nd=t[i];//node
	if(nd.r<l||nd.l>r)//完全不包含 
		return 0;
	
	if(nd.l>=l&&nd.r<=r)//完全包含 
		return nd.s;
		
	else//部分包含 
	{
		int ans=0;
		int m=(nd.l+nd.r)/2;
		if(m>=l)
			ans+=gs(lc,l,r);
		if(m+1<=r)
			ans+=gs(rc,l,r);
		
		return ans;
	}
}
signed main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	bt(1,1,n);
	while(m--)
	{
		int op,x,y;
		cin>>op>>x>>y;
		if(op==1)
		{
			int k;
			cin>>k;
			ud(1,x,y,k);
		}
		else
			cout<<gs(1,x,y)<<endl;
	}
	
	return 0;
}