SVD奇异值分解
下面是矩阵分解的一种方法——奇异值分解,设矩阵M是一个mXn的矩阵,则一定存在一个分解M=UWV,其中U是mXm的正交矩阵,V是nXn的正交矩阵,W是mXn的对角阵。如下图:
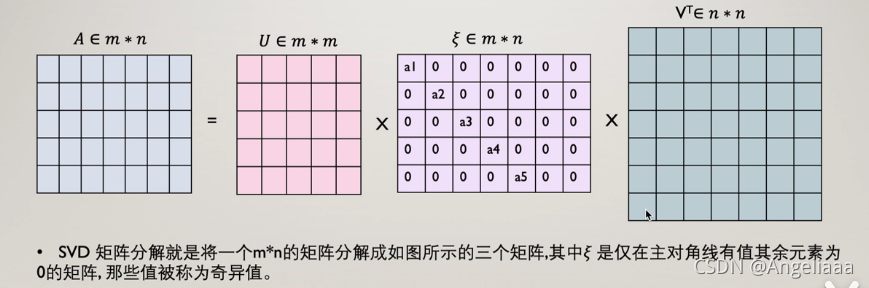
取对角阵中较大的k个元素作为隐含特征,删除对角阵中其他维度以及U和V中对应的维度,矩阵M就被分解为下面三个矩阵相乘,至此完成了隐向量维度为k的矩阵分解。
如果共现矩阵中1行5列的元素值为空,那个这个位置的元素值(也就是评分)就等于下图中横线位置的向量相乘。据此,就可预测出该位置用户对该物品的评分数值。
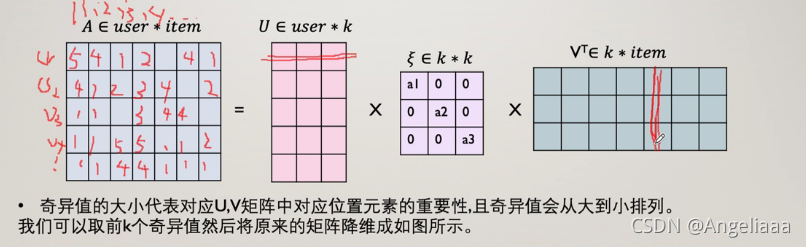
 本文介绍了奇异值分解(SVD)这一矩阵分解方法,它在推荐系统中用于预测用户对物品的评分。SVD将矩阵分解为正交矩阵U、对角阵W和正交矩阵V的乘积,通过保留对角阵中最大的k个奇异值来降低维度。这种方法利用全局信息生成隐向量,具备更好的泛化能力,相比协同过滤能处理冷启动问题。通过对共现矩阵的全局拟合,SVD能够预测任意用户和物品之间的评分,即使在原始数据中不存在交互记录。
本文介绍了奇异值分解(SVD)这一矩阵分解方法,它在推荐系统中用于预测用户对物品的评分。SVD将矩阵分解为正交矩阵U、对角阵W和正交矩阵V的乘积,通过保留对角阵中最大的k个奇异值来降低维度。这种方法利用全局信息生成隐向量,具备更好的泛化能力,相比协同过滤能处理冷启动问题。通过对共现矩阵的全局拟合,SVD能够预测任意用户和物品之间的评分,即使在原始数据中不存在交互记录。
下面是矩阵分解的一种方法——奇异值分解,设矩阵M是一个mXn的矩阵,则一定存在一个分解M=UWV,其中U是mXm的正交矩阵,V是nXn的正交矩阵,W是mXn的对角阵。如下图:

取对角阵中较大的k个元素作为隐含特征,删除对角阵中其他维度以及U和V中对应的维度,矩阵M就被分解为下面三个矩阵相乘,至此完成了隐向量维度为k的矩阵分解。
如果共现矩阵中1行5列的元素值为空,那个这个位置的元素值(也就是评分)就等于下图中横线位置的向量相乘。据此,就可预测出该位置用户对该物品的评分数值。

 1458
1458
 750
750
 8539
8539
 9841
9841
 1501
1501

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


