实验二 数列的极限

实验二 数列的极限

【实验目的】
（1）加深对数列极限概念的认识
（2）解决与极限有关的一些实际问题
数列极限的定义时高等数学的起点，理解和掌握它对于学好后面的内容极为重要.

§1 基本理论

1.1 数列极限的定义
1.2 数列极限存在准则

§2 实验内容与练习
2.1 对极限定义的认识
练习1

n=1:100;
a=n.^(n.^(-1));
plot(n,a,'.')

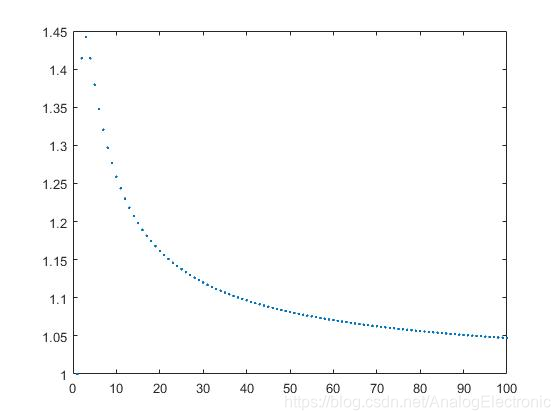
2.2 极限的计算

练习7

>> limit(exp(-1/x),x,0)
limit(exp(-1/x),x,0,'right')
limit(exp(-1/x),x,0,'left')
 
ans =
 
NaN
 
 
ans =
 
0
 
 
ans =
 
Inf

练习8

>> limit(sin(1/x),x,0)
 
ans =
 
NaN

练习9

>> limit((n+1)^(n+1)/((n+2)*n^n),n,inf)
 
ans =
 
exp(1)

练习10

>> limit(sin(x)/x,x,0)
 
ans =
 
1

>> limit(n*sin(1/n),n,inf)
 
ans =
 
1

>> limit(sqrt(n)*sin(1/sqrt(n)),n,inf)
 
ans =
 
1

>> limit(n^2/(n+1)*sin((n+1)/n^2),n,inf)
 
ans =
 
1

练习12

s=1;xn=1;yn=2;n=1;
while abs(s/n-yn)>10^(-3)
n=n+1
xN=xn;yN=yn;
xn=sqrt(xN*yN);yn=(xN+yN)/2;
s=s+xn;
fprintf('n=%g,xn=%5.3f,an=%5.3f\n',n,xn,s/n)
end

2.4 极限的应用
价格影响产量，产量影响价格，某城市
1997年猪肉产量40万吨，肉价为6.00元/公斤.
1998年猪肉产量35万吨，肉价为8.00元/公斤.
1998年猪肉产量38万吨
假定产量与价格是线性关系，问若干年以后猪肉的生产量与价格是否会趋于稳定？

clear a b c d;
[a,b]=solve('6=40*a+b','8=35*a+b');
[c,d]=solve('35=6*c+d','38=8*c+d');
x0=39;
for n=1999:1999+30
y0=a*x0+b;x0=c*y0+d;
fprintf('%g,%8.6f,%8.6f\n',n,eval(y0),eval(x0));
end

>> for n=1:100
if isprime(n)
fprintf('%g ',n)
end
end