如何计算根号之牛顿迭代法

之前上课时，老师提出了一个问题，在不借助自带函数的情况下，如何使用数学方法计算带根号的数字，并将其精确到小数点后3位，而最近正好阅读到了牛顿迭代法相关的内容，废话不多说，开始。

而牛顿迭代法的精华就是下列公式，这里不多介绍数学上的原理，而注重于实现

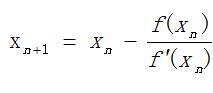
举个例子，假设有一个函数为y = x*x -5，要找到x最其根值，即令y=0，从而求出x为正负根号5，

那么如何让根号5精度到小数点后几位就是要处理的问题

计算如下：

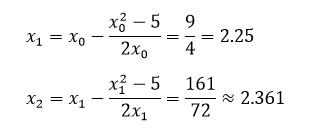
代码如下

#include <stdio.h>
#include<math.h>
double func1(double x)
{
	return x*x - 5.0;
}
double func2(double x)
{
	return 2*x;
}
int Newton(double *input,int k,double precision)
{
	double x1,x0;
	int num;
	x0 = *input;
	
	for(num=0;num<=k;num++)
	{
		if(func1(x0) == 0.0)
			return 0;
		x1 = x0- func1(x0)/func2(x0);
		if(fabs(x1-x0) < precision || fabs(func1(x0) < precision))
		{
			*input = x1;
			return 1;
		}
		else
		{
			x0 = x1;
		}
		printf("%lf\n",x1);
	}
	return 0;
}
int main(void)
{
    //precision为精度，input为初值，k为迭代的次数
	double input,precision = 0.01;
	int k = 20;
	scanf("%lf",&input);
	Newton(&input,k,precision); 
	printf("value:%lf",input);
		
}