PyTorch中卷积模块

原创已于 2024-12-10 22:11:26 修改 · 2.4k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #神经网络 #深度学习 #卷积神经网络

于 2024-12-01 16:50:23 首次发布

文章目录

常规卷积模块

以Conv2d为例，在PyTorch官方文档中，这个类的输入参数如下：

torch.nn.Conv2d(in_channel,out_channel,kernel_size,stride=1,padding=0,dilation=1,groups=1,bias=True,
padding_mode='zeros',device=None,dtype=None)

对于一个形状为 $N,C_{in},H,W)$ 的张量输入，输出张量的形状为 $N,C_{out},H_{out},W_{out})$ , 这里的 $C_{in}$ 对应上面的in_channel， $C_{out}$ 对应上面的out_channel，N是batch size。 $(H, W)$ 和 $H_{out},W_{out})$ 的对应关系由卷积步长、padding方式等决定（后面再讲）。
这里需要注意的是Conv2d处理的输入张量为四维，第二维是通道数，有时候，只有一个通道，如果要用conv2d就要增加一个维度，x.unsqueeze(1)；而Conv1d处理的数据维度是三维，(N, channels, length)

初始化一个卷积模块最常用的参数
stride：控制卷积的步长，是一个数字或元组(tuple)

如果是一个整数，表示卷积核再输入特征图上每次移动的步幅在水平方向和垂直方向是相同；如果是一个元组（a,b），则表示卷积核在高度方向和宽度方向移动的步幅分别为a和b。

padding：控制对输入使用的padding数，可以是字符串{“valid”,“same”}，可以是一个整数，也可以是一个整数元组，对应在相应边上padding的数量。

提供单个整数：会将这个值用于所有边界，宽和高都会加上这个值，例如，padding=2，会在所有边界上扩充两个元素作为填充
提供一对整数：第一个用于高度（上和下），第二个用于宽度（左和右），例如，padding=(1,2)，会在高度方向各添加一个元素（上下都加一个），宽度方向上加两个元素（左右都加两个）
提供一个四元组：会分别对应于（上、下、左、右），例如，padding=(1,1,2,2)，会在上边界添加一个元素，在下边界添加一个元素，在左边界添加两个元素，右边界添加两个元素。

dilation：控制卷积核点之间的空间。可以在保持参数量不变的情况下，扩大感受野。

例如，将dilation设置为2，那么卷积核中的元素将每隔一个单位采样一个点，感受野会扩大，但是卷积核中的参数数量不变。

groups：分组卷积需要用到的参数，用于控制输入和输出之间的连接。
padding_mode：用于指定对输入数据进行填充（padding）是所采用的模式。

“zeros”：零填充，在输入数据的边界上填充0
“reflect”：反射填充，输入数据的边界会反射到填充区域，例如，如果输入数据是[1,2,3,4]，反射填充后变成[2,1,3,4,3]
“replicate”：复制填充，输入数据的边界值会被复制到填充区域，例如，输入数据是[1,2,3,4]，复制填充后变成[1,1,2,3,4,4]
“circular”：循环填充，输入数据的边界会以循环的方式填充，例如，如果输入数据是[1,2,3,4]，循环填充后变成[4,1,2,3,4,1]

如何控制padding数量，以保持输出特征图大小与输入特征图大小相同？
下面是一个针对方形卷积核的通用的公式：
$padding=(\frac{K-1}{2}\times{dilation}-\frac{K-1}{2})\times stride$
其中：

K是卷积核大小（对于正方形卷积核， $K$ 既是高度也是宽度）
$d i l a t i o n$ 是扩张率
$s t r i d e$ 是步长

这里得到的padding值就是直接作为nn.Conv2d中参数padding，即在上下左右边界添加padding个元素。

分组卷积

分组卷积就是利用groups参数做到的，传统卷积中，卷积核与所有通道的元素做点乘再相加，做到了所有通道信息的融合，而分组卷积是将输入特征图在特征通道维度分成多组，每一组用一组卷积进行运算，然后拼接在一起，这样做减少了计算量和参数量，但是不同组通道的信息相互独立。分组卷积是深度可分离卷积的基础。
传统卷积核的维度，高和宽由kernel_size定义，而通道数与输入特征图相同，如下图所示：
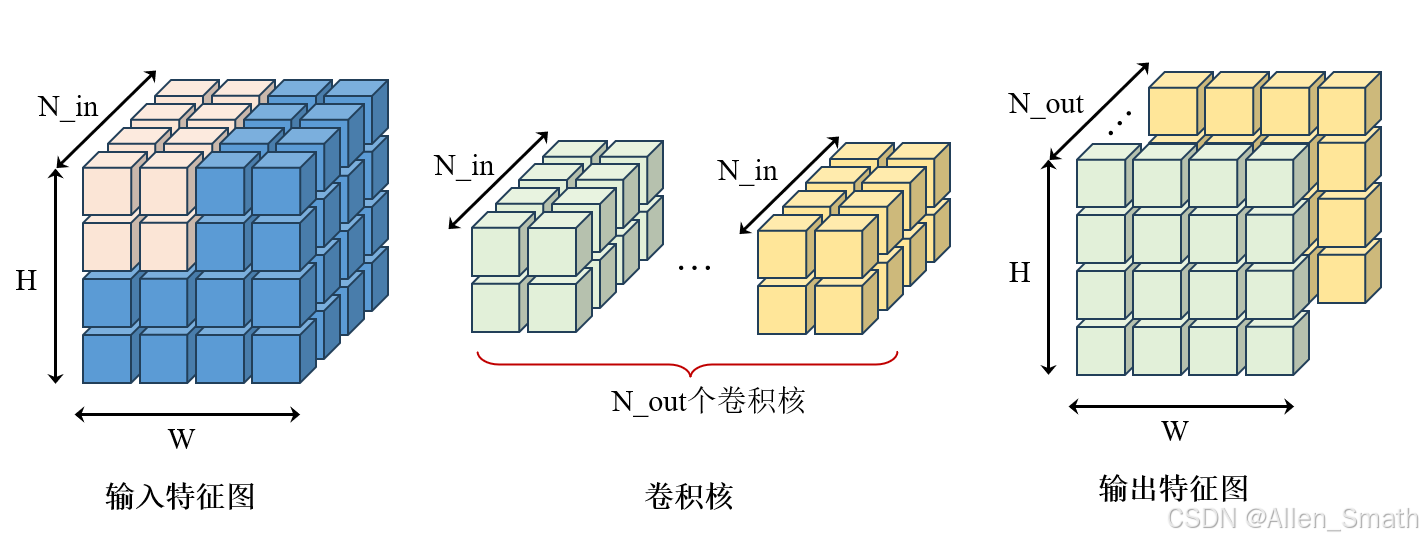
在这里插入图片描述
假设groups=2，分组卷积示意图如下：

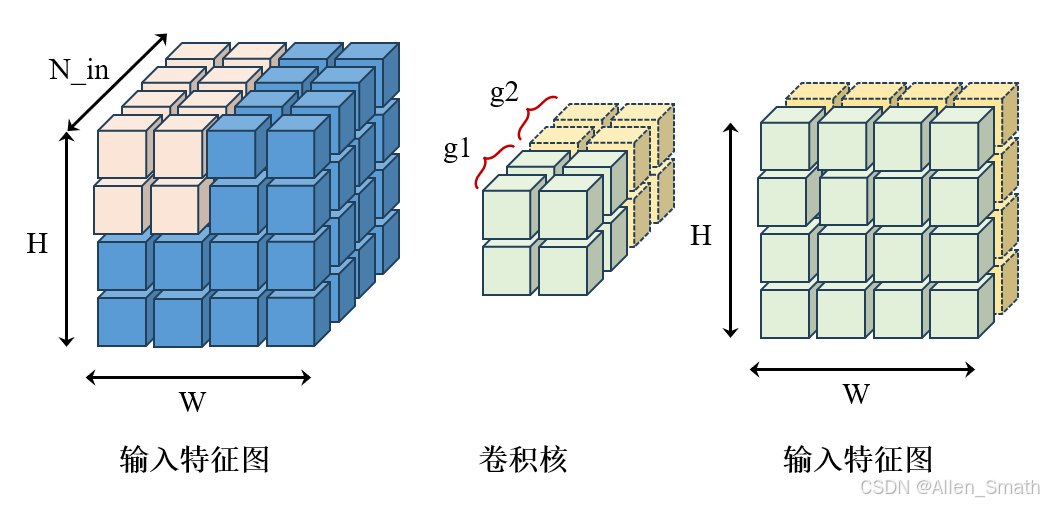
从图中可以看出，使用分组卷积groups=2时，首先将输入特征图在通道维度上分成两组，原本通道为 $N_{in}$ 的卷积核也分成了两组，分别独立进行卷积后，输出特征图在通道维度上进行拼接。也就是说，原本一个卷积核的参数量，产生了两个通道的输出特征图，之前需要 $N_{out}$ 个卷积核，现在每组只需要 $\frac{N_{out}}{2}$ 个卷积核。
使用分组卷积时，输入通道数和输出通道数必须得是分组数的倍数，例如，groups=2，那么输出通道数必须得是2的倍数，输入通道也必定能被2整除。
关于分组卷积能够降低卷积参数量和计算量的定量证明