透视投影和正交投影

最新推荐文章于 2024-11-23 10:59:29 发布

AllenWuuuu

最新推荐文章于 2024-11-23 10:59:29 发布

阅读量2.7k

点赞数 2

CC 4.0 BY-SA版权

文章标签：算法

本文链接：https://blog.youkuaiyun.com/AllenWuuuu/article/details/120761008

本文解析了如何通过相机位姿变换，将世界坐标系的三维点转换为相机坐标系下的点，随后进行透视投影，将它们映射到二维裁剪空间。介绍了投影矩阵的推导过程，涉及相机内参、相似三角形原理及具体公式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

世界坐标系下的点坐标，经过相机位姿变换之后，得到的相机坐标系下的点坐标，依然是三维空间中的点坐标，通过投影变换将其映射至二维空间坐标。

透视投影

透视投影将相机坐标系下的空间点映射至新的坐标空间，将相机坐标系下的视锥体，重映射成单位正方体的裁剪空间。视锥空间以外的点，全部作为无效点，也不会被投影至剪裁空间。

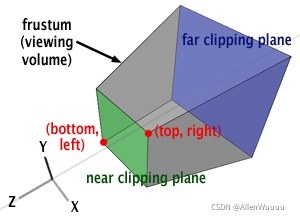
** 相机坐标系中原点是透镜 **

投影变换矩阵

$M= \left[ \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{matrix} \right ]$

其中近端剪裁平面的角点 $(l,b)$ 以及 $(r,t)$ ，近端裁剪平面和远端裁剪平面深度分别为 $-n$ 和 $-f$ 。

相机坐标系点 $P$ 经过透视投影后对应的裁剪空间点 $P^{per}$ ，透视投影过程如下：

$\left[ \begin{matrix} {P}' \\ -P_z \end{matrix} \right ]=M\left[ \begin{matrix} P \\ 1 \end{matrix} \right ]$

$\left[ \begin{matrix} P^{per} \\ 1 \end{matrix} \right ]= -\frac{1}{P_z} \left[ \begin{matrix} {P}' \\ -P_z \end{matrix} \right ]$

推导

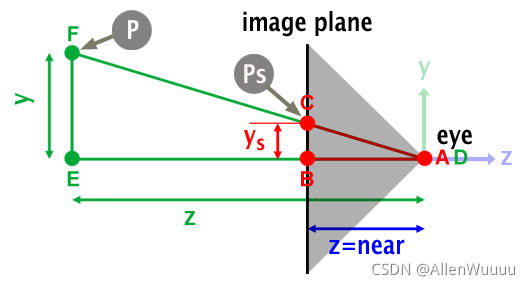
相机坐标系下点 $P$ 在投影平面（近端剪裁平面）上的投影点 $P_s$ ，根据相似三角形关系

$P_{s_y}=\frac{n \cdot P_y}{-P_z}$

$P_{s_x}=\frac{n \cdot P_x}{-P_z}$

又 $b \leq P_{s_y} \leq t$ ，即 $-1 \leq P_{y}^{per} = \frac{2P_{s_y}}{t-b} - \frac{t+b}{t-b} \leq 1$

$\therefore -1 \leq P_{y}^{per}= \frac{{P}'_{s_y}}{-P_z} = \frac{\frac{2n}{t-b}P_y}{-Pz} + \frac{\frac{t+b}{t-b}P_z}{-P_z} \leq 1$

        同理

$\therefore -1 \leq P_{x}^{per}= \frac{{P}'_{s_x}}{-P_z} = \frac{\frac{2n}{r-l}P_x}{-Pz} + \frac{\frac{r+l}{r-l}P_z}{-P_z} \leq 1$

构造齐次坐标

$\left[ \begin{matrix} {P}'_{s_x} \\ {P}'_{s_y} \\ {P}'_{s_z} \\ -P_z \\ \end{matrix} \right ] = \left[ \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & A & B \\ 0 & 0 & -1 & 0 \end{matrix} \right ] \left[ \begin{matrix} P_x \\ P_y \\ P_z \\ 1 \\ \end{matrix} \right ]$

$\left[ \begin{matrix} P_x ^{per} \\ P_y ^{per} \\ P_z ^{per} \\ 1 \end{matrix} \right ]=-\frac{1}{P_z} \left[ \begin{matrix} {P}'_{s_x} \\ {P}'_{s_y} \\ {P}'_{s_z} \\ -P_z \\ \end{matrix} \right ]$

        按照上式，希望得到A和B

$-1 \leq P_{z}^{per}= \frac{{P}'_{s_z}}{-P_z} = \frac{A P_z}{-Pz} + \frac{B}{-P_z} \leq 1$

$\begin{cases} \frac{A*(-n)}{n}+\frac{B}{n}=-1 \\ \frac{A*(-f)}{f}+\frac{B}{f}=1 \end{cases}$

        解得

$\begin{cases} A=-\frac{f+n}{f-n} \\ B=-\frac{2fn}{f-n} \end{cases}$

        所以最终的投影变换矩阵

$M= \left[ \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{matrix} \right ]$