决策树

决策树的构建，就是从训练数据集中归纳出一组分类规则，使它与训练数据矛盾较小的同时具有较强的泛化能力。有了信息增益来量化地选择数据集的划分特征，使决策树的创建过程变得容易，主要分几步：

1.计算数据集划分前的信息熵

2.遍历所有未作未划分条件的特征，分别计算根据每个特征划分数据集后的信息熵

3.选择信息增益最大的特征，并使用这个特征作为数据划分节点来划分数据

4.递归地处理被划分后的所有子数据集，从未被选择的特征里继续选择最优数据划分特征来划分子数据集

终止条件：1.特征用完了。2.信息增益足够小了

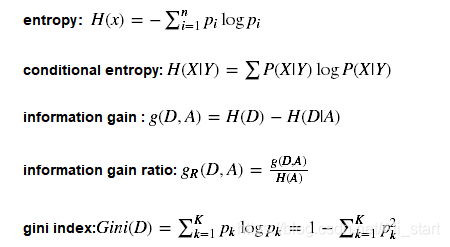
class DTree:
    def __init__(self, epsilon=0.1):
        self.epsilon = epsilon
        self._tree = {}

    # 熵
    @staticmethod
    def calc_ent(datasets):
        data_length = len(datasets)
        label_count = {}
        for i in range(data_length):
            label = datasets[i][-1]
            if label not in label_count:
                label_count[label] = 0
            label_count[label] += 1
        ent = -sum([(p/data_length)*log(p/data_length, 2) for p in label_count.values()])
        return ent

    # 经验条件熵
    def cond_ent(self, datasets, axis=0):
        data_length = len(datasets)
        feature_sets = {}
        for i in range(data_length):
            feature = datasets[i][axis]
            if feature not in feature_sets:
                feature_sets[feature] = []
            feature_sets[feature].append(datasets[i])
        cond_ent = sum([(len(p)/data_length)*self.calc_ent(p) for p in feature_sets.values()])
        return cond_ent

    # 信息增益
    @staticmethod
    def info_gain(ent, cond_ent):
        return ent - cond_ent

    def info_gain_train(self, datasets):
        count = len(datasets[0]) - 1
        ent = self.calc_ent(datasets)
        best_feature = []
        for c in range(count):
            c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
            best_feature.append((c, c_info_gain))
        # 比较大小
        best_ = max(best_feature, key=lambda x: x[-1])
        return best_

    def train(self, train_data):
        """
        input:数据集D(DataFrame格式)，特征集A，阈值eta
        output:决策树T
        """
        _, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:, -1], train_data.columns[:-1]
        # 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回T
        if len(y_train.value_counts()) == 1:
            return Node(root=True,
                        label=y_train.iloc[0])

        # 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回T
        if len(features) == 0:
            return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])

        # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
        max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
        max_feature_name = features[max_feature]

        # 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返回T
        if max_info_gain < self.epsilon:
            return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])

        # 5,构建Ag子集
        node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature)

        feature_list = train_data[max_feature_name].value_counts().index
        for f in feature_list:
            sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name], axis=1)

            # 6, 递归生成树
            sub_tree = self.train(sub_train_df)
            node_tree.add_node(f, sub_tree)

        # pprint.pprint(node_tree.tree)
        return node_tree

    def fit(self, train_data):
        self._tree = self.train(train_data)
        return self._tree

    def predict(self, X_test):
        return self._tree.predict(X_test)

离散化：

决策树是分类模型，对于连续值做离散化处理：比如<40为低，40-80为中，>80为高。

正则化：

加一个正则化参数，或者使用信息增益比 来作为特征选择的标准

过拟合：

剪枝：前剪枝（设定一个信息熵的阈值，停止创建分支）、后剪枝（在决策树构造完成后，对拥有同样父节点的节点，信息熵增加如果小于某个阈值，就剪掉）

 

数据预处理：包括数据读取；选择需要的数据；量化数据；缺失值填补

def red_dataset(fname):
    #指定第一列为行索引
    data = pd.read_csv(fname,index_col=0)
    #丢弃无用的数据
    data.drop(['Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
    #处理性别数据
    data['Sex'] = (data['Sex'] == 'male').astype('int')
    #处理登船港口数据   即将离散型的数据转换成 0 到 n−1 之间的数，
    #这里 n 是一个列表的不同取值的个数，可以认为是某个特征的所有不同取值的个数。
    lables = data['Embarked'].unique().tolist()
    data['Embarked'] = data['Embarked'].apply(lambda n:lables.index(n))
    #处理缺失值
    data = data.fillna(0)
    return data
train = red_dataset("C:/Users/DELL/Desktop/finish/sklearn/titanic/train.csv")
print(train)

提出标签数据；分割数据集

from sklearn.model_selection import train_test_split
y = train['Survived'].values
X = train.drop(['Survived'], axis=1).values

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

print('{0}; {1}'.format(X_train.shape, X_test.shape))

调用模型训练验证

from sklearn.tree import DecisionTreeClassifier

clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
train_score = clf.score(X_train,y_train)
test_score = clf.score(X_test,y_test)

print('train score:{0}; test score:{1}'.format(train_score,test_score))
#train score:0.9887640449438202; test score:0.8044692737430168   过拟合了

 画图

from sklearn.tree import DecisionTreeClassifier
#选择参数max_depth
def cv_score(d):
    clf = DecisionTreeClassifier(criterion='gini',min_impurity_decrease=d)
    clf.fit(X_train,y_train)
    tr_score = clf.score(X_train,y_train)
    cv_score = clf.score(X_test,y_test)
    return (tr_score, cv_score)

depths = range(2,30)
scores = [cv_score(d) for d in depths]

tr_score = [s[0] for s in scores]
cv_score = [s[1] for s in scores]

best_score_index = np.argmax(cv_score)
best_score = cv_score[best_score_index]
best_param = depths[best_score_index]
print('{};{}'.format(best_param, best_score))

#画图
plt.figure(figsize=(6,4),dpi=144)
plt.grid()
plt.plot(depths,cv_score,'g+')
plt.plot(depths,tr_score,'r')
plt.legend()