【线性代数】第四章——线性方程组

大法师安东尼ds

于 2020-07-25 17:14:32 发布

阅读量1.2k

点赞数

CC 4.0 BY-SA版权

文章标签：线性代数

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/Algo_x/article/details/107479929

数学基础专栏收录该内容

7 篇文章

订阅专栏

本章深入解析线性方程组的基础知识，包括线性方程组的定义、系数矩阵与增广矩阵的概念，重点讲解利用初等变换解线性方程组的方法。涵盖齐次与非齐次线性方程组的解法，通过典型例题剖析解的性质及求解技巧，强调解空间、基础解系的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本章体系

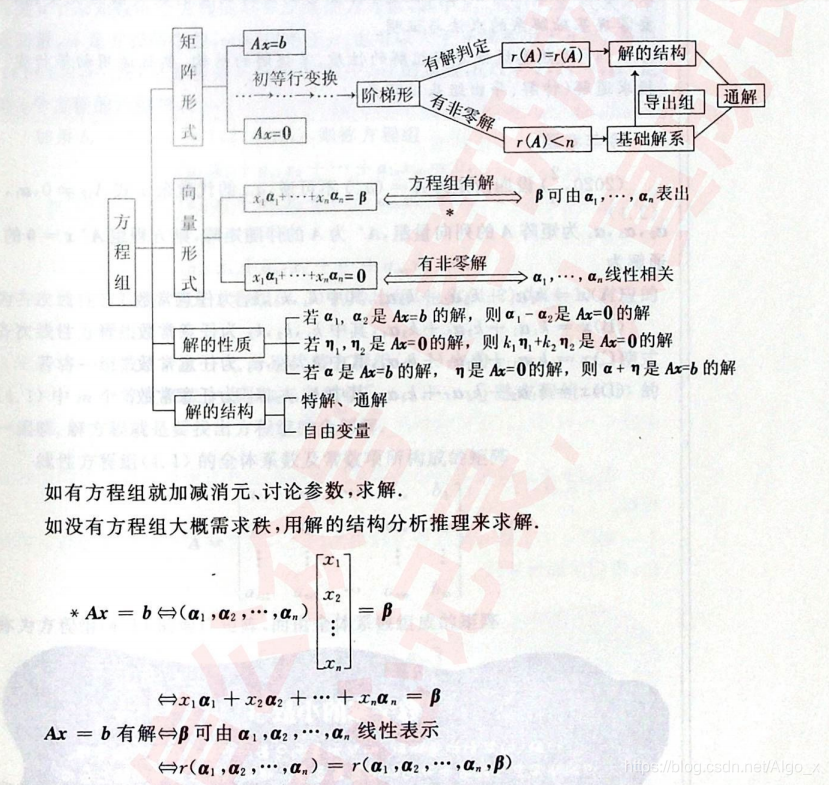
在这里插入图片描述

基础知识

线性方程组的定义

在这里插入图片描述

系数矩阵&增广矩阵

在这里插入图片描述

利用初等变换解线性方程组

在这里插入图片描述

基础解系

在这里插入图片描述

主要定理

梯形矩阵和解的关系

在这里插入图片描述
注意：仅仅是进行初等行变换，解线性方程组。

齐次线性

在这里插入图片描述

注意：
推论二从行列式角度给出了有解的充分必要条件
如何判断是否有无穷多解？唯一解？

解的性质

在这里插入图片描述

常考题型

考察基础解系所含向量的数量——维数公式

在这里插入图片描述

考察利用初等行变换和取特殊点求解线性方程组

例题 1——齐次方程

在这里插入图片描述
打洞，化为阶梯型，利用维数公式确定主元和自由变元。

例题 2——非齐次齐次通解+非齐次特解

通解的结构
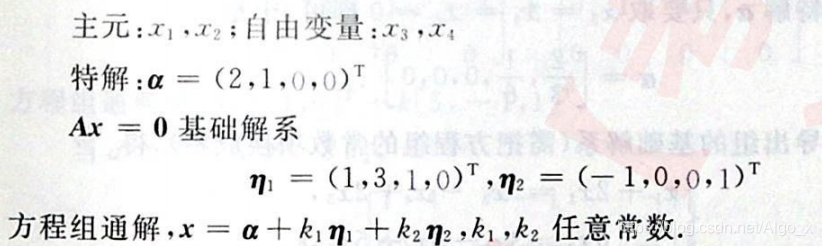
在这里插入图片描述

例题 3

在这里插入图片描述

定性判断方程组的解

例题 1

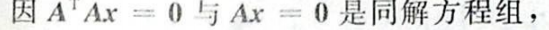
在这里插入图片描述

例题 2——利用行列式判断齐次方程组&n*n（克拉默法则）

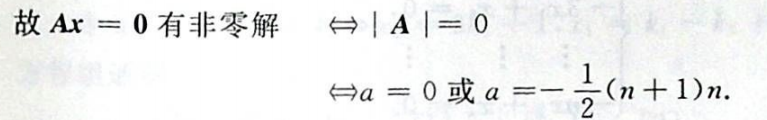
在这里插入图片描述

在这里插入图片描述

例题 3——非齐次

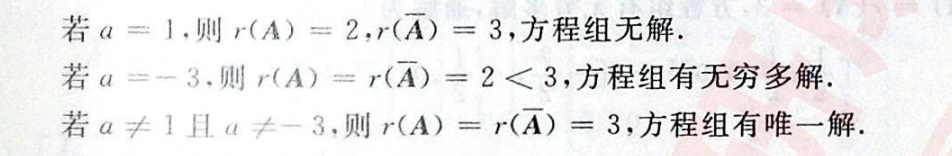
在这里插入图片描述

例题 4——非齐次，利用子式/解空间向量判断秩

在这里插入图片描述

利用解的结构求通解——绕开繁琐的计算

例题 1

在这里插入图片描述

例题 2

在这里插入图片描述

例题 3

在这里插入图片描述

例题 4

在这里插入图片描述

方程组无解

在这里插入图片描述

在这里插入图片描述
注意：是必要条件，还需再次检验

方程组同解

在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。