洛谷P3384 【模板】重链剖分/树链剖分题解

最新推荐文章于 2026-01-03 02:32:32 发布

原创最新推荐文章于 2026-01-03 02:32:32 发布 · 1.8k 阅读

37 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #数据结构

一、算法介绍：

树链剖分是一个在信息学竞赛中使用很频繁的算法，其通过将树分割成若干条链的形式，维护树上路径的信息。树链剖分由很多种形式，如重链剖分，长链剖分以及实链剖分等，此处只涉及重链剖分。

重链剖分可以将树上任意一条路径划分成不超过 $log⁡n\log n$ 条连续的链，每条链上的点深度互不相同。

重链剖分能保证划分出的每条链上的节点 dfs 序连续，因此可以使用线段树等对序列进行维护的数据结构来维护树上路径的信息。除此之外，重链剖分还经常用于实现其他功能，如求最近公共祖先等。

定义：

重子节点：对于每个非叶节点，定义其子节点中子树最大的子节点（如有相同任取起义）为重子节点。
轻子节点：对于每个非叶节点，定义其子节点中除重子节点外其余所有子节点为轻子节点。
重边：对于每个非叶节点，定义其与其重子节点之间的边为重边。
轻边：对于每个非叶节点，定义其与其轻子节点之间的边为轻边。
重链：定义若干条首尾衔接的重边构成的链为重链。落单的节点也视为重链。

如图：

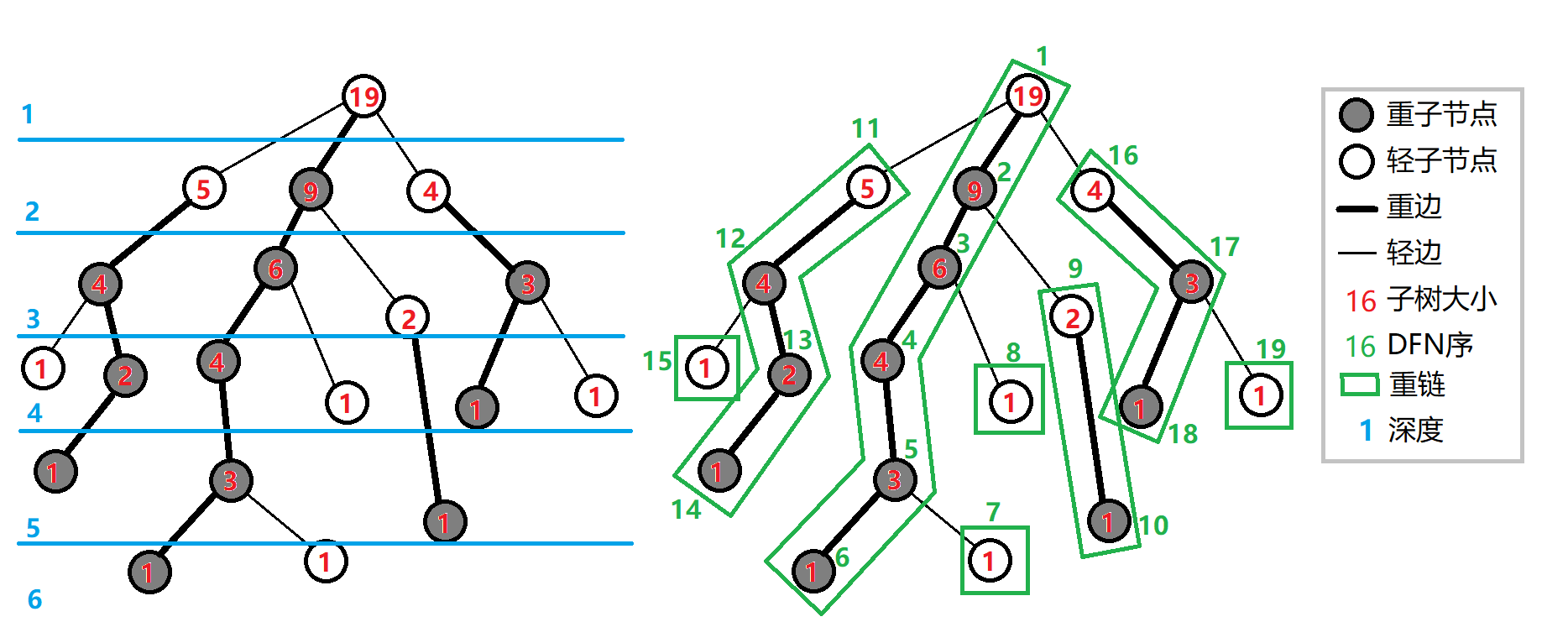
（图片来自 OI Wiki）

二、代码实现：

树链剖分的实现由两个 dfs 构成。

第一个 dfs 记录每个节点的父节点、深度、子树大小、重子节点，第二个 dfs 记录每个节点所在链的顶端，dfs 序以及 dfs 序所对应的节点的编号。
以下为代码实现，细节包含在注释中：

int fa[N],top[N],son[N],size[N],deep[N],w[N],dfn[N],cnt_tree;
void dfs1(int x){
	size[x]=1;//标记每个节点的子树大小，初始为 1，因为包含节点本身
	int maxson=-1;//记录以重子节点为根的子树大小
	for(int i=head[x];i;i=t[i].next){
		int y=t[i].ver;
		if(y==fa[x]) continue;
		deep[y]=deep[x]+1,fa[y]=x,dfs1(y),size[x]+=size[y];//更新深度、子树大小、父节点等信息
		if(maxson<size[y]) maxson=size[y],son[x]=y;//维护重子节点
	}
}

void dfs2(int x){
	dfn[x]=++cnt_tree,w[cnt_tree]=a[x];//标记新编号并赋值到新数组中
	if(son[x]) top[son[x]]=top[x],dfs2(son[x]);//先处理重子节点
	for(int i=head[x];i;i=t[i].next){//按轻子节点递归处理
		int y=t[i].ver;
		if(y==fa[x]||y==son[x]) continue;
		top[y]=y,dfs2(y);//每个轻子节点有一条以其为起始的链
	}
}

三、问题解决

说完了树链剖分，是时候回到本题了。

容易发现，每一条重链和每一个子树中的节点的编号都是连续的。问题要求我们处理路径上与子树上的修改与查询，我们分成两类问题讨论：

路径上：

类似于倍增法求最近公共祖先的思想，两个节点不断向上跳，跳到其所在重链的顶端的父节点，每次处理所在链顶端深度更深的节点，直到跳到同一条重链上为止，沿途对每一条重链用线段树维护区间修改与查询。时间复杂度 $O(\log^2 n)$ 。
子树上：

由于子树的 dfs 序连续，修改或查询一个节点的子树只用处理这一段连续的 dfs 序区间，线段树维护即可。时间复杂度 $O(log⁡n)O(\log n)$ 。

正确性证明：

至于为什么这么做是对的，下面提供证明：

令 $x$ 和 $y$ 表示两个节点， $z$ 表示 $x$ 和 $y$ 的最近公共祖先，假设 $x$ 在 $z$ 所在的重链上且 $y$ 不在，则 $y$ 一定在 $z$ 的轻子节点的子树上，显然 $y$ 所在的重链深度一定更深，所以会优先跳 $y$ ，直到 $y$ 跳到 $z$ 为止。如都不在 $z$ 所在的重链上，上跳时总有一个会跳到 $z$ 所在的重链上。当二者都在该链上时，直接区间维护即可。如此，显然不会更新多余的节点，也不会有节点被漏掉。

时间复杂度：

1.重链数量

从任意节点到根的路径上，轻边的数量不超过 $log⁡n\log n$ 条，这是因为在每次经过轻边时，子树的大小至少减半，显然最多经过 $log⁡n\log n$ 条轻边。因此，每个路径拆解后重链不会超过 $log⁡n\log n$ 条。

2.单次操作复杂度分析

路径上操作：每条重链的区间操作通过线段树实现，复杂度为 $O(log⁡n)O(\log n)$ 。最多会经过 $log⁡n\log n$ 条重链，故总时间复杂度为 $O(\log n) × O(\log n) = O(\log^2 n)$ 。

子树上操作：该操作只需进行一次线段树的区间修改或查询，复杂度为 $O(log⁡n)O(\log n)$ 。

四、通过代码：

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define ls(p) p<<1
#define rs(p) p<<1|1
const int N=1e5+10;

namespace IO{//快读快写
	inline int read(){
		int x=0,f=1;
		char ch=getchar();
		while(ch<'0'||ch>'9'){
			if(ch=='-') f=-1;
			ch=getchar();
		}
		while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
		return x*f;
	}

	inline void write(int x){
		if(x<0){
			putchar('-');
			x=-x;
		}
		if(x>9) write(x/10);
		putchar(x%10+'0');
	}
}

using namespace IO;

namespace code{
	int n,m,R,P,a[N];
	
	int head[N],tot;
	
	struct edge{//链式前向星存图
		int ver,next;
	}e[N<<1];
	
	void add(int x,int y){//加边
		e[++tot].ver=y,e[tot].next=head[x],head[x]=tot;
	}
	
	int fa[N],son[N],deep[N],size[N],w[N],dfn[N],top[N],cnt;
	
	void dfs1(int x){//树剖预处理
		size[x]=1;
		int max_son=-1;
		for(int i=head[x];i;i=e[i].next){
			int y=e[i].ver;
			if(y==fa[x]) continue;
			fa[y]=x,deep[y]=deep[x]+1;
			dfs1(y);
			size[x]+=size[y];
			if(size[y]>max_son) max_son=size[y],son[x]=y;
		}
	}
	
	void dfs2(int x,int fr){
		dfn[x]=++cnt,w[cnt]=a[x],top[x]=fr;
		if(son[x]) dfs2(son[x],fr);
		for(int i=head[x];i;i=e[i].next){
			int y=e[i].ver;
			if(y==fa[x]||y==son[x]) continue;
			dfs2(y,y);
		}
	}
	
	struct segment_tree{//线段树
		struct node{
			ll sum,lazy;
		}t[N<<2];
		
		void push_up(int p){
			t[p].sum=(t[ls(p)].sum+t[rs(p)].sum)%P;
		}
		
		void push_down(int p,int l,int r){
			int mid=(l+r)>>1;
			t[ls(p)].sum=(t[ls(p)].sum+t[p].lazy*(mid-l+1))%P,t[ls(p)].lazy=(t[ls(p)].lazy+t[p].lazy)%P;
			t[rs(p)].sum=(t[rs(p)].sum+t[p].lazy*(r-mid))%P,t[rs(p)].lazy=(t[rs(p)].lazy+t[p].lazy)%P;
			t[p].lazy=0;
		}
		
		void build(int p,int l,int r){
			if(l==r) return t[p].sum=w[l]%P,void();
			int mid=(l+r)>>1;
			build(ls(p),l,mid),build(rs(p),mid+1,r);
			push_up(p);
		}
		
		void add(int p,int l,int r,int al,int ar,ll k){
			if(al<=l&&r<=ar) return t[p].sum=((ll)t[p].sum+k*(r-l+1))%P,t[p].lazy=((ll)t[p].lazy+k)%P,void();
			int mid=(l+r)>>1;
			push_down(p,l,r);
			if(al<=mid) add(ls(p),l,mid,al,ar,k);
			if(ar>mid) add(rs(p),mid+1,r,al,ar,k);
			push_up(p);
		}
		
		ll query_sum(int p,int l,int r,int ql,int qr){
			if(ql<=l&&r<=qr) return t[p].sum;
			ll mid=(l+r)>>1,ret=0;
			push_down(p,l,r);
			if(ql<=mid) ret=((ll)ret+query_sum(ls(p),l,mid,ql,qr))%P;
			if(qr>mid) ret=((ll)ret+query_sum(rs(p),mid+1,r,ql,qr))%P;
			return ret;
		}
	}t;
	
	void solve1(int x,int y,int z){//路径上修改
		while(top[x]!=top[y]){
			if(deep[top[x]]<deep[top[y]]) swap(x,y);
			t.add(1,1,n,dfn[top[x]],dfn[x],z),x=fa[top[x]];
		}
		if(deep[x]>deep[y]) swap(x,y);
		t.add(1,1,n,dfn[x],dfn[y],z);
	}
	
	void solve2(int x,int y){//路径上查询
		int ret=0;
		while(top[x]!=top[y]){
			if(deep[top[x]]<deep[top[y]]) swap(x,y);
			ret=((ll)ret+t.query_sum(1,1,n,dfn[top[x]],dfn[x]))%P,x=fa[top[x]];
		}
		if(deep[x]>deep[y]) swap(x,y);
		ret=(ret+t.query_sum(1,1,n,dfn[x],dfn[y]))%P;
		write(ret),putchar('\n');
	}
	
	void solve3(int x,int z){//子树上修改
		t.add(1,1,n,dfn[x],dfn[x]+size[x]-1,z);
	}
	
	void solve4(int x){//子树上查询
		write(t.query_sum(1,1,n,dfn[x],dfn[x]+size[x]-1)),putchar('\n');
	}

	void solve(){
		n=read(),m=read(),R=read(),P=read();
		for(int i=1;i<=n;i++) a[i]=read();
		for(int i=1;i<n;i++){
			int x=read(),y=read();
			add(x,y);
			add(y,x);
		}
		dfs1(R),dfs2(R,R),t.build(1,1,n);
		while(m--){
			int op=read(),x=read(),y,z;
			if(op==1) y=read(),z=read(),solve1(x,y,z);
			else if(op==2) y=read(),solve2(x,y);
			else if(op==3) z=read(),solve3(x,z);
			else solve4(x);
		}
	}
}

int main(){
	code::solve();
	return 0;
}