2022 CCF CSP-J2 解密

原创已于 2022-11-09 09:41:42 修改 · 792 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #数据结构

于 2022-11-09 02:13:42 首次发布

算法题专栏收录该内容

11 篇文章

订阅专栏

这篇博客介绍了一种算法来处理正整数问题，通过询问次数，找到满足ni=p*q且c*d=p*q-p-q+2的整数pi和qi。关键步骤包括计算t=c*d和p+q=n-t+2的解决方案，最后提供了C++代码实现。

给定一个正整数 $k$ ，有 $k$ 次询问，每次给定三个正整数 $n_i$ , $e_i$ , $d_i$ ，求两个正整数 $p_i,q_i$ ，使 $n_i = p_i × q_i$ ， $e_i × d_i = (p_i − 1)(q_i − 1) + 1$ 。

输入格式
第一行一个正整数 $k$ ，表示有 $k$ 次询问。
接下来 $k$ 行，第 i 行三个正整数 $n_i, d_i, e_i$ 。
输出格式
输出 $k$ 行，每行两个正整数 $p_i, q_i$ 表示答案。
为使输出统一，你应当保证 $p_i ≤ q_i$ 。

如果无解，请输出 NO。

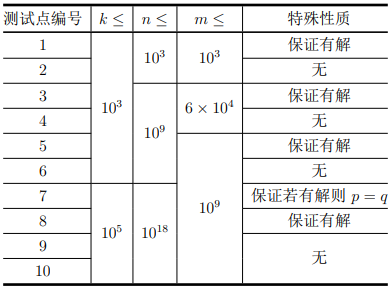
数据范围
以下记 $m = n - e \times d + 2$ 。
保证对于 $100%100\%$ 的数据， $1 ≤ k ≤ 10^5$ ，对于任意的 $1 \leq i \leq k$ ， $1 ≤ n_i ≤ 10^{18}$ ， $1 ≤ e_i × d_i ≤ 10^{18}$ ， $1 ≤ m ≤ 10^9$ 。

QQ截图20221107141520.png

输入样例：

输出样例：

2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88

C++代码

#include<bits/stdc++.h>
typedef long long LL;

using namespace std;

int main() {
    int tt;
    cin >> tt;
    
    while(tt --) {
        LL n, c, d, p, q;
        //n = p * q
        //c * d = p * q - p - q + 2
        //c * d = n - p - q + 2
        //t = c * d
        //p + q = n - t + 2
        //p * q = n
        cin >> n >> c >> d;
        LL t = c * d;
        LL s = n - t + 2;//p + q
        LL x = s * s;//(p + q) ^ 2
        LL y = x - 4 * n;//(p - q) ^ 2
        
        LL z = LL(sqrt(y));//|p - q|
        if(z * z != y) cout << "NO" << '\n';
        else {
            p = (s + z) / 2;
            q = (s - z) / 2;
            if(p > q) swap(p, q);
            cout << p << " " << q << '\n';
        }
    }
    
    return 0;
}