论文精读第三期：RL+LLM 进化史：为什么说 Verifier 是推理大模型的“第一块拼图”？-优快云博客

论文的阅读方式为：论文概览-->深入理解-->总结思考

在 GRPO 一统天下的今天，我们为什么要回过头看 2021 年的老论文？因为这篇论文揭示了一个计算与智能的底层定律：验证一个答案比生成一个答案要容易得多。 本文将从底层原理出发，探讨 OpenAI 是如何利用这个不对称性，通过“海选+验证”的暴力美学，为后来的 o1 和推理模型奠定基石的。

论文概览

一、研究背景与动机

当前的大规模语言模型（如GPT-3）在许多任务上已接近人类水平，但在多步数学推理任务中仍表现不稳定。模型生成解答时，一旦出现错误，往往无法自我修正，导致最终答案错误。论文指出，若仅依赖生成式方法，可能需要极大的模型参数量才能达到理想效果，因此需要探索更高效的扩展方法。

二、GSM8K数据集

论文提出了一个高质量的数学应用题数据集GSM8K，包含8.5K个小学生水平的数学问题，具有以下特点：

高质量：由人工编写，通过严格质量控制，错误率低于2%。
高多样性：避免模板化问题，确保每个问题在语言和结构上具有独特性。
中等难度：问题需2-8步解决，涉及基本算术运算，适合研究模型推理能力。
自然语言解答：解答以自然语言形式提供，而非纯数学表达式，便于分析模型的推理过程。

三、方法：验证器（Verification）

1. 基线方法：微调（Finetuning）

直接对模型进行微调，使用语言建模目标生成单一解答。
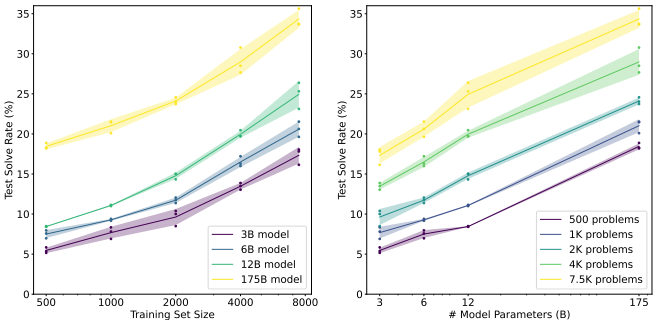
实验发现，即使使用175B参数的模型，在GSM8K上的表现仍不理想。要达到80%的正确率，可能需要模型规模扩大30倍或训练数据增加两个数量级。

2. 验证器方法

核心思想：训练一个验证器来评估模型生成的多个解答的正确性，并选择得分最高的解答作为最终答案。
流程：
1. 微调一个生成器（generator）模型，用于生成候选解答。
2. 对每个问题生成100个解答，并标记其正确性。
3. 训练验证器，使其能判断解答的正确性。
关键优势：
- 验证任务比生成任务更简单，且能通过多候选答案筛选提升性能。
- 验证器在数据量充足时表现显著优于微调方法。

四、实验结果与分析

1. 验证器显著提升性能

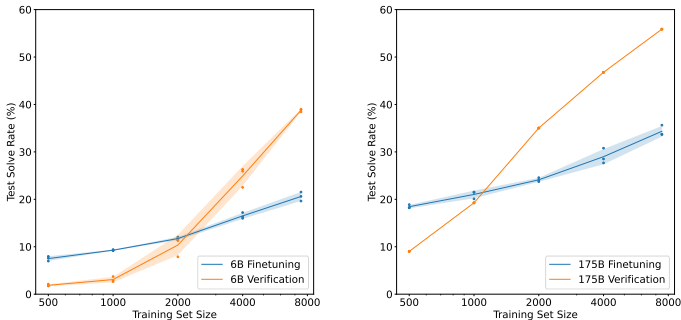
使用6B参数的验证器，性能略优于175B参数的微调模型，相当于30倍模型规模的提升。
验证器在数据量增大时扩展性更好，而微调方法随数据增加性能提升缓慢。

2. 验证器消融实验

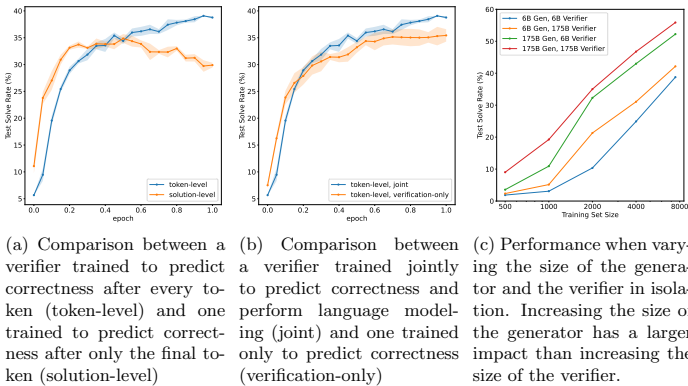
Token级验证器优于Solution级：Token级验证器对每个token进行预测，虽训练更困难，但能更好地捕捉推理过程中的错误，避免过拟合。
联合训练目标更有效：结合语言建模目标和验证目标，能提升验证器的判别能力。
验证器可小于生成器：即使验证器参数远小于生成器，仍能有效筛选答案，说明验证器可能依赖启发式规则而非全面推理。

3. 测试时计算资源权衡

生成过多候选答案（如超过400个）可能因对抗性样本而降低性能，100个候选答案是计算成本与性能的平衡点。
对Top-K个答案进行投票（如K=3~5）可进一步提升性能。

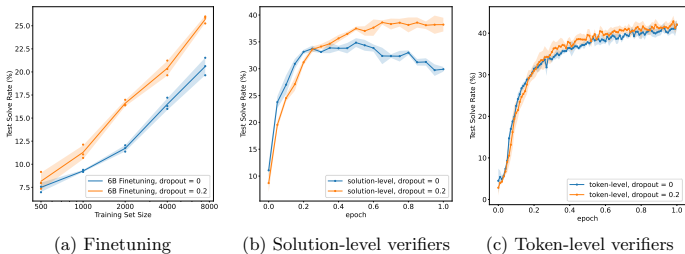
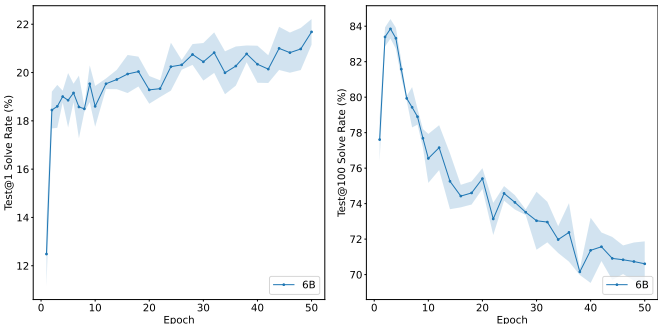
4. 正则化（Dropout）的作用

对模型添加20%的Dropout能显著缓解过拟合，尤其在Solution级验证器中效果明显。

五、技术细节

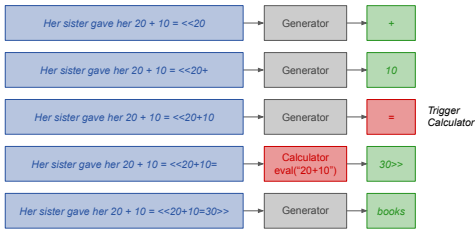
1. 计算器注解（Calculator Annotations）

训练时注入计算注解，测试时模型可调用计算器执行精确运算，减少算术错误。
注解通过Python eval函数实现，错误时回退到模型生成。

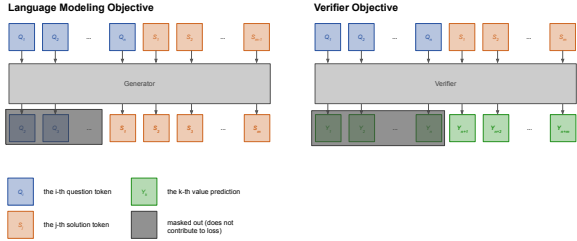
2. 验证器架构

验证器基于语言模型，增加一个标量输出头，用于预测每个token的正确性概率。
训练时联合优化语言建模损失和验证损失。

六、结论与展望

验证器方法在数学推理任务中显著优于传统微调，且扩展性更好。
Token级验证器抗过拟合能力更强，Dropout能进一步提升性能。
未来可探索验证器在更复杂数学问题上的应用，GSM8K数据集将支持更多研究。

深入理解

第一部分：直觉与基石

核心痛点：为什么LLM做不好数学？

语言模型本质上是概率模型。在处理文本生成（比如写诗、聊天）时，模糊性是可以接受的，甚至是有益的。

但在多步数学推理中，存在两个致命问题：

误差级联 (Error Cascading): 这是一个自回归生成的问题。如果模型在第一步计算 2+2=5，那么后续基于这个结果的所有推理，即使逻辑完美，最终答案也是错的。
缺乏自我纠正: 标准的自回归语言模型（GPT-3时代）通常是一条路走到黑，很难在生成过程中“回头看”并修正自己的错误。

这其实非常符合计算理论中的直觉：生成一个证明（寻找解的路径）通常属于 NP困难问题，而验证一个证明是否正确通常是 P问题（多项式时间可解）。 OpenAI 的核心就在于：训练模型去“判卷”，比训练模型去“做题”更有效率。

解决方案：生成器 (Generator) vs. 验证器 (Verifier)

为了解决上述痛点，论文提出了两种截然不同的解决思路。

方案 A: 标准微调 (Fine-Tuning)

这是最直观的方法。将题目作为 Input，将正确的推导过程和答案作为 Label，使用交叉熵损失函数（Cross-Entropy Loss）进行微调。

目标: 让模型模仿人类的推导过程。
缺点: 模型往往只是在“模仿语气”，而不是真正理解逻辑。对于未见过的题目，泛化能力差。

方案 B: 验证器 (Verification) —— 本文的核心

这个方法引入了 Test-time Search (推理时搜索) 的概念。

流程如下：

生成 (Generate): 让模型对同一个问题生成 N 个不同的候选解。这里的 N 可以很大（例如100个）。
验证 (Verify): 训练一个独立的 Verifier (验证器) 模型（或者同一个模型的不同Head），给这 N个候选解打分。
选择 (Select): 选择得分最高的那个解作为最终答案。

数学表达:

假设题目是 x，模型生成的解是 y。

我们不是直接最大化 $P(y|x)$ ，而是训练一个打分函数 $V(x, y) \rightarrow [0, 1]$ ，用来评估 y 是正确答案的概率。

最终输出为：

$\hat{y} = \operatorname*{arg\,max}_{y \in \text{samples}} V(x, y)$

数据集的革命：GSM8K

在2021年之前，数学数据集要么太简单（比如简单的算术题），要么太形式化（比如代数证明）。OpenAI 意识到我们需要一个既包含语言多样性，又包含多步逻辑推理的数据集。

GSM8K (Grade School Math 8.5K) 应运而生：

规模: 8,500 个题目。
难度: 小学水平（Grade School），通常需要 2 到 8 个步骤解决。
关键特征:
- 高质量链式思维 (Chain of Thought): 所有的答案都包含了自然的语言解释，而不仅仅是公式。例如：“Sally有3个苹果，吃掉了1个，所以剩下 3-1=2 个。”
- 语言差异: 题目虽然数学逻辑简单，但题面叙述方式多变，强迫模型理解语义，而不是死记硬背公式模版。

GSM8K 的出现，实际上为 Process Supervision (过程监督) 和 Outcome Supervision (结果监督) 提供了一个绝佳的实验场。因为数学题不仅有最终答案（Answer），还有中间过程（Reasoning Steps）。这篇论文主要关注的是结果验证，但它为后来的 Let's Verify Step by Step (Process Reward Model) 铺平了道路。

到目前为止，我们确立了这篇论文的核心哲学： “与其费力训练一个天才做题家，不如训练一个大规模海选系统，并配备一个合格的阅卷老师。”

这是一种用计算换智能 (Compute for Intelligence) 的策略。我们通过在推理阶段（Inference Time）生成大量的样本并进行筛选，来弥补模型单次生成能力的不足。

第二部分：技术实现 (Implementation Mechanics)

整个训练流程分为三个关键阶段：生成器微调 (Generator SFT) ， 采样与数据构造 (Sampling) ， 验证器训练 (Verifier Training)。

1. 训练生成器 (The Generator)

这步非常标准，目的是为了获得一个“还算不错”的初始解空间。

模型: GPT-3 (6B 或 175B 参数)。
数据: GSM8K 的训练集。
目标函数: 标准的自回归语言模型损失 (Cross-Entropy Loss)。

$\mathcal{L}_{\text{gen}} = -\sum_{t} \log P(y_t | x, y_{<t})$

其中 x是问题，y 是包含思维链 (Chain of Thought) 的完整解答。

此时的模型只是一个“模仿者”。它学会了按照步骤说话，但经常一本正经地胡说八道。

2. 构造验证器数据集 (Dataset Construction for Verifier)

这是这篇论文最精彩的工程细节之一。验证器不能只看人类写的“标准答案”，它必须学会判断“模型生成的各种错误答案”。它需要见多识广。

我们使用上一步训练好的 Generator 来生成数据：

1.大规模采样: 对于 GSM8K 训练集中的每一个问题 $x$ ，使用 Generator 采样 100 个不同的解答 $\{y_1, y_2, ..., y_{100}\}$ 。

关键点: 需要设置较高的 Temperature（例如 0.7），保证生成的多样性。如果 Temperature 太低，生成的解都一样，验证器就学不到东西了。

2.自动标注 (Labeling):

我们将这 100 个生成的解答的最终答案提取出来。
与 Ground Truth (标准答案) 进行比对。
标签分配:
- 如果最终答案正确，标记为 Correct (1)。
- 如果最终答案错误，标记为 Incorrect (0)。

3.数据构成: 现在的训练数据变成了三元组 $(x, y_{\text{generated}}, \text{label})$ 。

特别注意 (Technical Nuance):

这是一个 Outcome-based (基于结果) 的监督信号。即使中间步骤推理错了，但如果碰巧撞对了最终答案（False Positive），在这个阶段也会被标记为 Correct。这是 Outcome RM 的一个固有弱点，也是后来 Process RM (PRM) 想要解决的问题。

3. 训练验证器 (The Verifier)

验证器 V的架构通常与生成器相同（或者稍小）。它的任务是评估 $P(\text{correct} | x, y)$ 。

训练目标: 这是一个二分类问题。
Input: [问题] + [候选解]
Output: 一个标量分数（Score），代表该解是正确的概率。
Loss Function:

$\mathcal{L}_{\text{ver}} = - \mathbb{E}_{(x,y,l) \sim \mathcal{D}} \left[ l \cdot \log V(x,y) + (1-l) \cdot \log (1 - V(x,y)) \right]$

其中 $l \in \{0, 1\}$ 是标签。

实现细节:

在实际操作中，OpenAI 并没有加一个额外的 Linear Head，而是直接微调语言模型，让它在序列末尾预测一个特殊的 Token（比如 "True" 或 "False"）的概率。

4. 推理阶段：Test-Time Compute (测试时计算)

模型训练好了，如何使用？这里就涉及到了 Inference-time Search。

当一个新的测试题 $x_{test}$ 进来时：

Generate: 使用 Generator 生成 N 个候选解（例如 N=100）。
Score: 使用 Verifier 给N 个解分别打分。
Rank: 按分数排序。
Select: 选择分数最高的解作为最终输出。

$\hat{y} = \operatorname*{arg\,max}_{y \in \{y_1...y_N\}} V(x_{test}, y)$

深入分析：Verifier 到底强在哪？

我们看数据背后的原理。论文中展示了几个关键的 Scaling Laws 现象：

1. 覆盖率 (Coverage) vs. 准确率

Generator 的准确率可能只有 20%（即 Top-1 准确率）。
但是，如果我们看 Top-100 个解中是否存在一个正确答案（这被称为 Coverage），通过率可能高达 80%！
结论: Generator 其实很有潜力，它“能”做对，只是经常发挥失常。Verifier 的作用就是把这个潜在的正确答案从垃圾堆里找出来。

2. 验证器的 Scaling (参数量)

论文发现了一个有趣的现象：强验证器 + 弱生成器 > 弱验证器 + 强生成器。

即使 Generator 比较弱（参数小），只要 Verifier 足够聪明，能够识别出那偶然出现的正确答案，系统的整体性能就会大幅提升。
这暗示了：对于数学问题，判别 (Discrimination) 比生成 (Generation) 具有更高的算力性价比。

3. 性能提升幅度

在 GSM8K 上，引入 Verifier 后，性能从单纯 Fine-tuning 的基线大幅提升。

比如，对于 175B 的模型，单纯 Finetuning 准确率约为 33%。
加上 Verifier (Best-of-100) 后，准确率飙升至 55% 左右。
这在当时是一个巨大的飞跃。

虽然这篇论文是开山之作，但从 2025 年的视角（你现在的视角）来看，它有什么局限性？

算力浪费: 推理时需要生成 100 个样本才能选出 1 个，计算成本增加了 100 倍。这在实时应用中是昂贵的。
Outcome RM 的局限: 刚才提到了，它只看结果。如果模型逻辑完全错误但答案蒙对了（例如： $2+2=5, 5-1=4$ ），Verifier 会给它高分。这会导致“奖励黑客 (Reward Hacking)”现象，模型会学到通过错误的路径凑出对的数字。
独立性假设: Generator 和 Verifier 是分开训练的。Generator 并没有因为 Verifier 的存在而变得更强（除非我们用 RL，比如 PPO，把 Verifier 的分值回传给 Generator，但这篇论文还没做这一步）。

第三部分：深远影响与演进 (Impact & Evolution)

1. 致命缺陷：结果主义的陷阱 (The ORM Limitation)

这篇论文提出的 Verifier 被称为 ORM (Outcome-supervised Reward Model)，因为它只看最后那个数字对不对。

你肯定知道 Reward Shaping（奖励塑造）的难点。ORM 有两个显著缺陷：

虚假相关 (Spurious Correlation): 模型可能通过错误的逻辑推导出正确的答案（撞大运）。ORM 会奖励这种错误逻辑。
- 例子: 题目是 2+2=4。模型输出：“因为今天是星期四，所以答案是 4。” ORM 打分：1.0 (Correct)。
稀疏奖励 (Sparse Reward): 在复杂的长链条推理中，只有最后一步有信号。中间所有的推理步骤都没有直接的反馈。这使得 Generator 很难学习到究竟是哪一步走错了。

演进方向:

这就是为什么 OpenAI 后来发表了另一篇极其重要的论文 "Let's Verify Step by Step" (Lightman et al., 2023)。它提出了 PRM (Process-supervised Reward Model)。这是我们明天要看的论文

区别: PRM 不仅看结果，还人工标注每一个推理步骤（Step）是 Correct, Incorrect 还是 Neutral。
优势: PRM 提供了密集的奖励信号，彻底解决了“逻辑错误答案正确”的问题。

2. 从 Best-of-N 到 PPO：闭环的形成

在这篇论文中，OpenAI 仅仅使用了 Rejection Sampling (Best-of-N)。

Generator 的参数在测试时是固定的。
Verifier 只是作为一个过滤器。

这其实是 RLHF 的雏形，但还没有“闭环”。

我们通常会更进一步：

我们将 Verifier 作为一个真正的 Reward Function，使用 PPO (Proximal Policy Optimization) 算法来更新 Generator 的参数。

$\theta_{new} \leftarrow \text{PPO}(\theta_{old}, \text{RewardFromVerifier})$

这样，Generator 就会内化 Verifier 的判别能力，逐渐学会直接生成高分（正确）的解，而不需要每次都生成 100 个来浪费算力。这篇论文是构建那个 Reward Function 的第一步。

3. 哲学升华：System 1 vs. System 2

这篇论文最深刻的启示在于它触及了认知科学的核心：卡尼曼的双系统理论 (Daniel Kahneman's System 1 & 2)。

System 1 (快思考): 直觉、快速、无意识。对应 Generator (LLM 直接生成)。
System 2 (慢思考): 逻辑、费力、有意识。对应 Verifier + Search (推理时计算)。

这篇论文证明了： 仅仅扩大 System 1（把模型做大）在数学推理上边际收益递减；而引入 System 2（生成-验证-搜索）可以解锁极其强大的逻辑能力。

OpenAI o1 的本质： 目前的推测是，o1 模型通过强化学习（RL），学会了在内部进行这种“生成-验证-修正”的循环。它不再是简单的 Best-of-N，而是学会了Chain of Thought with Self-Correction。它在输出最终答案前，已经在内部进行了成千上万次的隐式验证。