算法基础教学第二步：数组（超级详细原理级别讲解）

原创 已于 2025-12-02 17:06:01 修改 · 1.3k 阅读 · 26 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #链表 #数据结构 #神经网络

于 2025-12-02 17:04:12 首次发布

第一部分：从内存物理结构看数组的本质

1. 计算机的“记忆”：内存（RAM）

想象一下，你的计算机内存（RAM）并不是一个神秘的黑盒子，而是一条无限长的、笔直的街道。

  • 单元格（Cell）： 这条街上有一排排的“小房子”。在计算机中，每一个“小房子”只能存放 1个字节（Byte = 8 bits） 的数据。

  • 地址（Address）： 为了能找到这些房子，每个房子都有一个唯一的门牌号。

    • 第1个房子的地址是 0x0000

    • 第2个房子的地址是 0x0001

    • ...以此类推。

关键点： 计算机访问内存是“随机访问”（Random Access）的。这意味着，计算机读取地址 0x0000 的数据，和读取地址 0x9999 的数据，花费的时间是完全一样的。这一特性是数组高效的物理基础。

2. 数据的“体型”

在这一长排房子里，如果我们要住进去不同的“人”（数据类型），占用的空间是不一样的：

  • char (字符): 很瘦，只需要 1 个字节（占用 1 个房子）。

  • int (整数): 比较胖，通常需要 4 个字节（连续占用 4 个房子）。

  • double (双精度浮点数): 很壮，通常需要 8 个字节（连续占用 8 个房子）。

从底层看变量： 当你声明一个整数 int a = 10; 时，操作系统会在内存街上找 4 个空闲的连续房子（比如地址 100 到 103），把 10 这个数字的二进制形式塞进去，然后记下：“变量 a 住在门牌号 100”。

3. 数组的诞生：强迫症式的“连续居住”

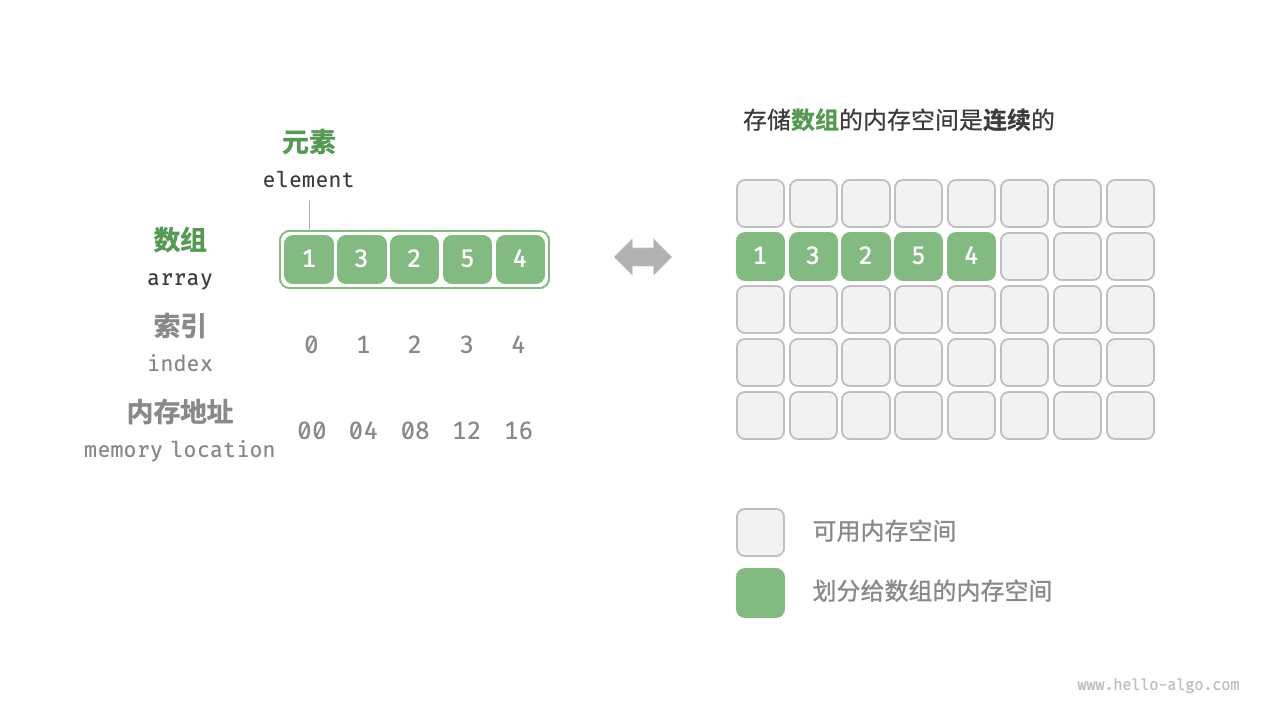
现在，我们终于可以定义什么是数组了。

从计算机组成原理的角度看，数组只有两个铁律：

  1. 同构性： 所有元素必须是相同类型（大家占用的空间必须一样大，比如都是 int）。

  2. 连续性： 所有元素在内存中必须紧挨着排列，中间不能有空隙。

假设我们要创建一个包含 3 个整数的数组：int arr[3]。

  1. 计算机首先问：“一个整数占多大？” 答案是 4 字节。

  2. 计算机接着算：“你要 3 个？那就是$3 \times 4 = 12$个字节。”

  3. 计算机去内存街上寻找一块连续的、长度为 12 个字节的空地。

假设它找到了从地址 2000 开始的空地。那么内存布局如下：

数组下标 (Index)内存实际地址 (Memory Address)存储内容备注
arr[0]2000整数的第1部分基地址 (Base Address)
2001...
2002...
2003整数的第4部分arr[0] 结束
arr[1]2004整数的第1部分
2005...
......
arr[1]2007整数的第4部分arr[1] 结束
arr[2]2008整数的第1部分
......
arr[2]2011整数的第4部分arr[2] 结束

4. 为什么数组下标从 0 开始？（核心数学原理）

很多初学者困惑，为什么不是 arr[1] 代表第一个元素？

这是因为数组的下标（Index），在底层逻辑里，代表的不是“第几个”，而是偏移量（Offset）。

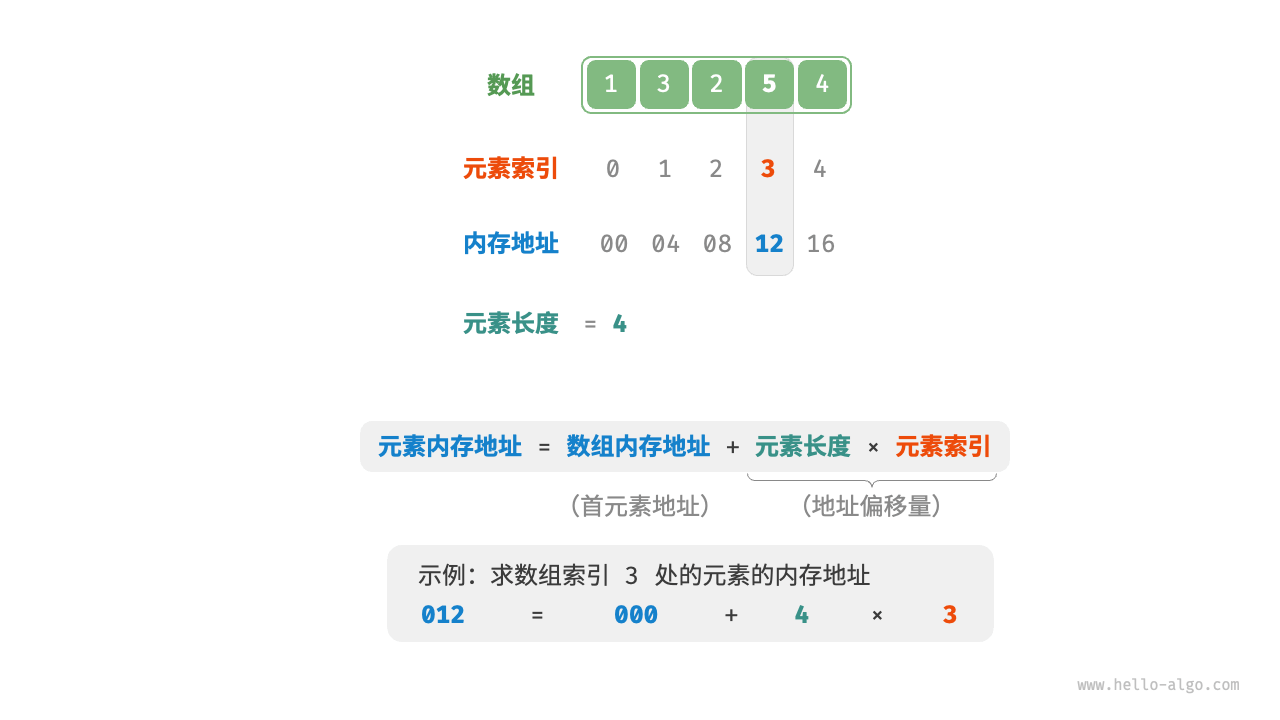
还记得我们之前说的吗？访问内存是非常快的。当我们想要访问 arr[2] 时，计算机不需要从头去数，它直接用一个公式算出地址：

$Target\_Address = Base\_Address + (Index \times Size\_of\_Element)$

带入我们的例子：

  • Base_Address (基地址): 2000 (即数组头部地址)

  • Index (下标): 2

  • Size_of_Element (元素大小): 4 字节

$Target = 2000 + (2 \times 4) = 2008$

计算机直接算出 2008，然后瞬间飞到那个地址去读取数据。

如果是从 1 开始计数会怎样？

公式就会变成：

$Target = Base + ((Index - 1) \times Size)$

看到那个 (Index - 1) 了吗？这意味着计算机每次访问数组都要多做一次减法运算。对于极度追求效率的底层硬件来说，这多余的一次指令是不可接受的浪费。

5. 数组的优缺点（基于硬件原理）

基于上面的结构，我们就能深刻理解它的特性：

  • 优点：查询神速（随机访问）。

    不管数组有一万个元素还是一个元素，访问 arr[9999] 和 arr[0] 的时间是一样的，因为只需要做一次乘法和一次加法就能算出地址。这在算法中被称为 $O(1)$ 时间复杂度。

  • 优点：CPU 缓存友好（Cache Locality）。

    这是进阶原理：CPU 读取内存时，不是只读 1 个字节，而是会把邻近的一块数据（Cache Line）都读进 CPU 缓存。因为数组是连续的，当你读 arr[0] 时，arr[1]、arr[2] 可能已经被顺手读进 CPU 缓存了，下次访问它们时速度会快几十倍。

  • 缺点：插入和删除极慢。

    如果你想在 arr[0] 和 arr[1] 之间插一个新的数字，因为内存必须是连续的，你必须把 arr[1] 及其后面所有的元素全部往后挪一个位置，给新来的腾地儿。这就像在一排紧挨着的书架中间硬塞一本书，后面的书都得动。

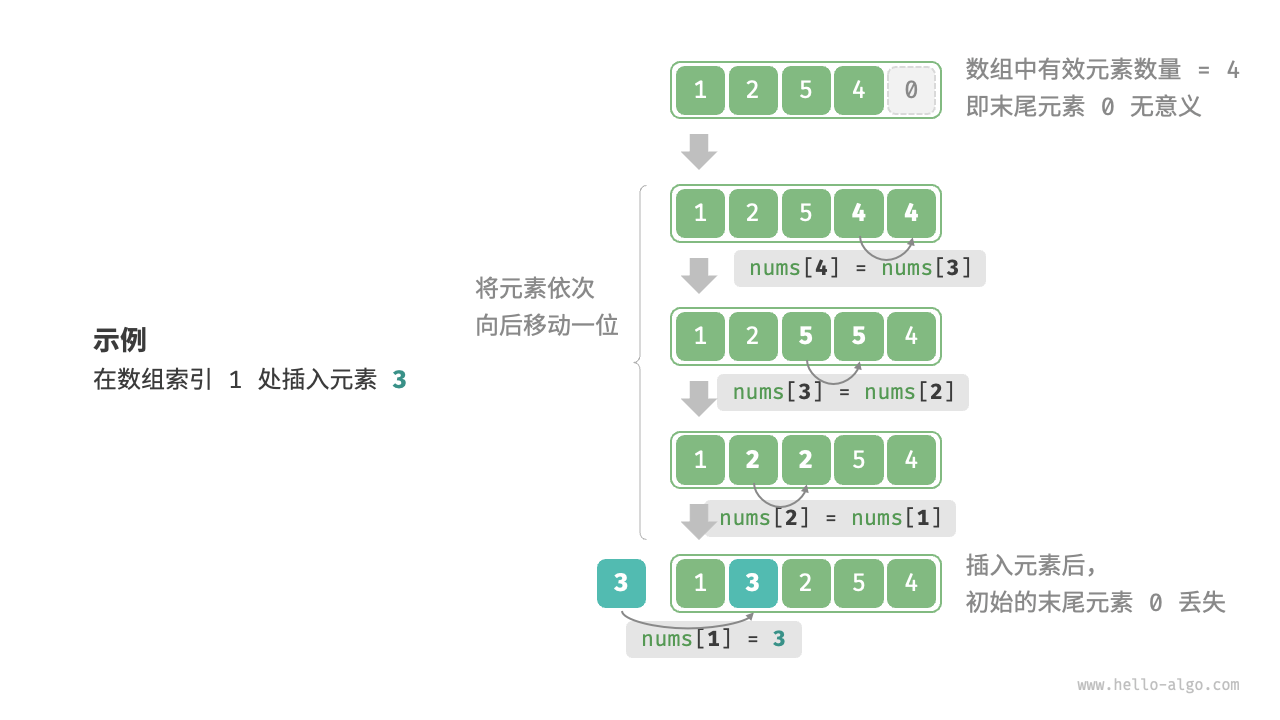
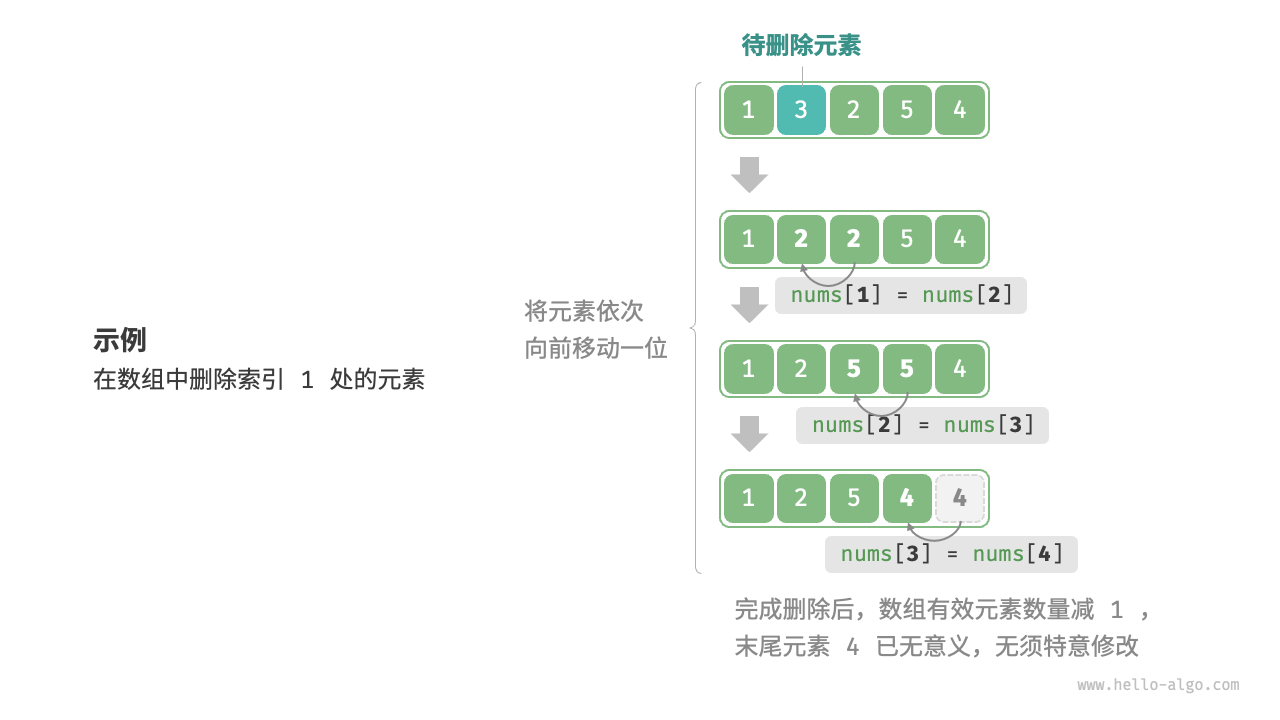
6.数组操作

初始化数组：

# 初始化数组
arr: list[int] = [0] * 5  # [ 0, 0, 0, 0, 0 ]
nums: list[int] = [1, 3, 2, 5, 4]

访问元素：

def random_access(nums: list[int]) -> int:
    """随机访问元素"""
    # 在区间 [0, len(nums)-1] 中随机抽取一个数字
    random_index = random.randint(0, len(nums) - 1)
    # 获取并返回随机元素
    random_num = nums[random_index]
    return random_num

插入元素：

def insert(nums: list[int], num: int, index: int):
    """在数组的索引 index 处插入元素 num"""
    # 把索引 index 以及之后的所有元素向后移动一位
    for i in range(len(nums) - 1, index, -1):
        nums[i] = nums[i - 1]
    # 将 num 赋给 index 处的元素
    nums[index] = num

删除元素

def remove(nums: list[int], index: int):
    """删除索引 index 处的元素"""
    # 把索引 index 之后的所有元素向前移动一位
    for i in range(index, len(nums) - 1):
        nums[i] = nums[i + 1]

遍历数组

def traverse(nums: list[int]):
    """遍历数组"""
    count = 0
    # 通过索引遍历数组
    for i in range(len(nums)):
        count += nums[i]
    # 直接遍历数组元素
    for num in nums:
        count += num
    # 同时遍历数据索引和元素
    for i, num in enumerate(nums):
        count += nums[i]
        count += num

查找元素：

def find(nums: list[int], target: int) -> int:
    """在数组中查找指定元素"""
    for i in range(len(nums)):
        if nums[i] == target:
            return i
    return -1

扩容数组

在复杂的系统环境中，程序难以保证数组之后的内存空间是可用的，从而无法安全地扩展数组容量。因此在大多数编程语言中，数组的长度是不可变的。

如果我们希望扩容数组，则需重新建立一个更大的数组，然后把原数组元素依次复制到新数组。这是一个O(n)的操作，在数组很大的情况下非常耗时。代码如下所示：

def extend(nums: list[int], enlarge: int) -> list[int]:
    """扩展数组长度"""
    # 初始化一个扩展长度后的数组
    res = [0] * (len(nums) + enlarge)
    # 将原数组中的所有元素复制到新数组
    for i in range(len(nums)):
        res[i] = nums[i]
    # 返回扩展后的新数组
    return res

7.数组典型的运用

数组是一种基础且常见的数据结构，既频繁应用在各类算法之中，也可用于实现各种复杂数据结构。

  • 随机访问：如果我们想随机抽取一些样本，那么可以用数组存储，并生成一个随机序列，根据索引实现随机抽样。
  • 排序和搜索：数组是排序和搜索算法最常用的数据结构。快速排序、归并排序、二分查找等都主要在数组上进行。
  • 查找表：当需要快速查找一个元素或其对应关系时，可以使用数组作为查找表。假如我们想实现字符到 ASCII 码的映射，则可以将字符的 ASCII 码值作为索引，对应的元素存放在数组中的对应位置。
  • 机器学习：神经网络中大量使用了向量、矩阵、张量之间的线性代数运算，这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。
  • 数据结构实现：数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如，图的邻接矩阵表示实际上是一个二维数组。

第一部分总结

从计算机组成原理来看，数组就是一块固定的、连续的内存区域。它的本质是用空间换时间——通过严格的排列限制，换取了极致的访问速度。我们可以初始化一个比较长的数组，只用前面一部分，这样在插入数据时，丢失的末尾元素都是“无意义”的，但这样做会造成部分内存空间浪费。

值得注意的是，由于数组的长度是固定的，因此插入一个元素必定会导致数组尾部元素“丢失”。我们将这个问题的解决方案留在“列表”章节中讨论。、

第二部分：动态扩容和引用存储

但是你可能会问：这不对啊！我在 Python 里写 ls = []，然后疯狂 append 往里塞数据，从来不需要管它多大，而且我还能往同一个数组里塞整数、字符串和对象。这是怎么回事？

1. 静态数组 vs. 动态数组（扩容的骗局）

在最底层的 C 语言（接近硬件）中，数组是“静态”的。

  • 场景： 你申请了 int arr[3]。

  • 内存： 操作系统给了你 12 个字节（3个整数的空间）。

  • 危机： 现在你想存第 4 个数字。

  • 结果： 内存溢出（Overflow）。你后面的内存地址可能住着别人的数据（比如操作系统的核心代码），你如果硬塞进去，程序会直接崩溃，甚至导致系统蓝屏。

为了解决这个问题，Python 的 list、Java 的 ArrayList、C++ 的 vector 引入了动态数组的概念。它们表面上看起来可以无限增长，其实背后在干“搬家”的苦力活。

幕后的“搬家”算法：

当你创建一个空数组时，Python 可能会悄悄预定一小块内存（比如能装 4 个位置）。

  1. 填满： 当你填入第 5 个元素时，数组满了。

  2. 寻找新房： 解释器（Python 的大脑）会立刻去内存街上找一块更大的空地。通常是原来大小的 1.125 倍或 1.5 倍（不同语言策略不同，假设是 2 倍）。

  3. 复制（Copy）： 解释器把旧房子里的 4 个元素，一个一个复制到新房子里。

  4. 销毁： 释放（删掉）旧房子的数据，把那块地还给操作系统。

  5. 插入： 终于把第 5 个元素放进新房子的空位里。

性能代价：

这就是为什么有时候 append 操作会突然变慢。平时插入是 O(1)（直接放进去），但一旦触发“搬家”，复杂度瞬间飙升到 O(N)（因为要复制 N 个旧数据）。

2. 怎么在这个“连续”的数组里存不同类型的数据？

这也是一个巨大的思维陷阱。

我在第一部分说过：数组要求所有元素大小必须一致（方便计算地址偏移量）。

  • int 是 4 字节。

  • string 可能几百字节。

  • Image 对象可能几兆字节。

如果 Python 允许 ls = [1, "hello", image_obj]，这三个东西大小完全不一样，那是怎么挤在同一个“连续”数组里的？

答案：它是“指针数组” (Array of Pointers)

Python 里的列表（List），实际上存的不是数据本身，而是数据的地址（门牌号）。

我们再回到内存街：

数据区（分散在各处）：

数字 1 被扔在内存地址 0x500。

字符串 "hello" 被扔在内存地址 0x800。

对象 image 被扔在内存地址 0x900。

数组区（连续整齐）： 你的 ls 数组，在内存中确实是连续的，但它里面存的内容是统一大小的地址卡片（在64位计算机上，一个地址通常占 8 字节）。

数组下标内存实际内容 (存储的是地址)指向哪里？
ls[0]0x500 指向数字 1
ls[1]0x800 指向字符串 "hello"
ls[2]0x900 指向对象

优点（灵活性）： 数组本身只需要维护整齐的“地址”，它不管地址指向的房子里住的是大象还是蚂蚁。这就是为什么 Python 列表可以存任何东西。

缺点（CPU 缓存失效 - Cache Miss）： 还记得第一部分说的“CPU 缓存友好”吗？

C 语言数组（紧凑）： 数据 1, 2, 3 紧挨着。CPU 一把抓过来，吃得很快。

Python 列表（引用）： 数组里只有地址。CPU 读 ls[0]，拿到地址，跑到 0x500 去读数据；接着读 ls[1]，拿到地址，又要跑到 0x800 去读数据。

后果： 这种跳来跳去的读取方式，打破了内存的局部性原理。CPU 必须频繁地等待内存响应，导致处理大规模数值计算时，Python 原生列表比 C 语言数组慢几十倍甚至上百倍。

第二部分总结

从计算机组成原理的视角来看：

  1. 并没有真正的“无限”数组： 所谓的无限增长，只是底层在不断地“申请更大内存 -> 搬家 -> 销毁旧家”。

  2. 并没有真正的“混合”数组： 所谓的混合类型，只是数组里存了一堆“地址指针”，指向了散落在内存各处的数据实体。

这也是为什么在 AI 和深度学习（如 PyTorch, TensorFlow, NumPy）中，我们绝对不会使用 Python 原生的 List 来做计算。我们会使用 Tensor（张量） 或 NumPy Array。

为什么？因为 Tensor 重新回归了第一部分的原则：它强制要求数据类型单一（比如全都是 float32），并且在内存中紧凑排列。只有这样，GPU 和 CPU 才能全速运转，进行大规模矩阵运算。

第三部分：多维数组的谎言 —— 内存是线性的

1. 内存没有“维度”

在你的代码里，你可能写过 int matrix[3][3]，把你脑海中的数据想象成一个像围棋棋盘一样的 3x3 网格。

但在计算机的物理层面上，二维数组根本不存在。

还记得第一部分讲的吗？内存是一条无限长的、笔直的街道（线性的一维结构）。计算机的硬件设计里没有“换行”这个概念，只有地址 0, 1, 2, 3, 4, ...。

所以，要在一个只有一维的内存条上存一个二维的矩阵，我们必须把这个矩阵“拍扁”，拉成一条直线。

这就引出了两种流派，决定了数据在底层是如何“拉直”的：行优先（Row-Major） 和 列优先（Column-Major）。

2. 行优先（Row-Major）—— C/C++, Python (NumPy) 的选择

这是最符合人类阅读习惯的方式：先填满第一行，再接第二行。

假设我们有一个 $2 \times 3$ 的数组（2行，3列）：

$\begin{bmatrix} A & B & C \\ D & E & F \end{bmatrix}$

内存里的实际排列：

计算机先把第一行 A, B, C 塞进内存，紧接着把第二行 D, E, F 塞进去。

内存地址0x1000x1040x1080x10C0x1100x114
存储数据ABCDEF
逻辑坐标[0,0][0,1][0,2][1,0][1,1][1,2]
底层寻址公式（核心数学）：

如果我要访问 matrix[i][j]（第 i 行，第 j 列），计算机怎么算出它在直直的内存街上的地址？

$Address = Base + (i \times \text{column} + j) \times Element\_Size$

  • $i \times \text{column}$：意思是“跳过前面的$i$ 整行”。

  • $+ j$：意思是“在当前行再往后走 $j$ 步”。

3. 列优先（Column-Major）—— Fortran, MATLAB, R 的选择

虽然 C 语言统治了世界，但在古老的科学计算领域（如 Fortran），它们选择把矩阵竖着切。

同样的矩阵：

$\begin{bmatrix} A & B & C \\ D & E & F \end{bmatrix}$

内存里的实际排列：

先存第一列 A, D，再存第二列 B, E，最后存第三列 C, F。

内存地址0x1000x1040x1080x10C0x1100x114
存储数据ADBECF
逻辑坐标[0,0][1,0][0,1][1,1][0,2][1,2]

如果你在 Python (行优先) 和 MATLAB (列优先) 之间传递数据，或者调用一些古老的线性代数库（如 BLAS/LAPACK），如果不注意这一点，你的矩阵就会转置（行列颠倒），导致计算结果完全错误。

4. 性能生死线：为什么循环的顺序很重要？

这一节是所有程序员进阶的分水岭。理解了它，你就能写出比别人快几倍的代码。

假设我们有一个巨大的二维数组 arr[10000][10000]，我们要遍历它求和。

写法 A（行遍历）：

// 外层是行，内层是列
for(int i=0; i<10000; i++) {
    for(int j=0; j<10000; j++) {
        sum += arr[i][j];
    }
}

写法 B（列遍历）：

// 外层是列，内层是行
for(int j=0; j<10000; j++) {
    for(int i=0; i<10000; i++) {
        sum += arr[i][j]; // 注意这里下标变化的是 i
    }
}

在数学上，A 和 B 是一样的。 在计算机底层，A 比 B 快几十倍 甚至更多。

原因：CPU 缓存行（Cache Line）与空间局部性

回到第一部分的知识：CPU 读内存不是一个字节一个字节读的，而是一次“抓一把”（通常是 64 字节，称为一个 Cache Line）。

对于写法 A（行优先）：

  1. 当 CPU 读 arr[0][0] 时，它很聪明地把 arr[0][0] 到 arr[0][15]（假设 int 是4字节，64/4=16个）全读进缓存了。

  2. 接下来计算 arr[0][1] 到 arr[0][15] 时，CPU 不需要再访问慢速的内存条，直接从高速缓存拿数据。

  3. 结果： 极高的缓存命中率（Cache Hit）。

对于写法 B（列优先）：

  1. 你先读 arr[0][0]。CPU 把 arr[0][0]...arr[0][15] 读进缓存。

  2. 但你下一个要读的是 arr[1][0]！

  3. arr[1][0] 在哪里？它在内存里距离 arr[0][0] 非常远（隔了一整行，也就是隔了 10000 个数据）。

  4. CPU 刚才辛辛苦苦读进来的 arr[0][1]... 完全没用到，就被迫扔掉，去加载 arr[1][0] 所在的新位置。

  5. 结果： 每一步都在“跳跃”。这就叫 Cache Thrashing（缓存颠簸）。CPU 大部分时间都在等内存条数据传输，而不是在计算。

5. 特别补充：Python List 的特殊情况

在 C 语言或 NumPy (np.array) 中，二维数组确实是一块连续的内存。

但是，普通的 Python List ([[1,2], [3,4]]) 并不是真正的二维数组，它是 "数组的数组" (Array of Arrays)。

  • 外层 List ls 存了两个指针（地址）。

  • 第一个指针指向一块内存（存了 [1, 2]）。

  • 第二个指针指向另一块完全不相关的内存（存了 [3, 4]）。

这两块内存不一定是连续的。所以在 Python 原生 List 里，行优先虽然也有优势，但不如 C/NumPy 中那么极其显著，因为无论怎么走，你都要进行两次“指针跳转”。

第三部分总结

  1. 物理无维度： 所有的多维数组在底层都是一维的。

  2. 映射规则： 行优先（Row-Major）是主流，但在跨语言交互时要小心列优先（Column-Major）。

  3. 性能铁律： 永远顺着内存布局的方向遍历数组。对于 C/C++/Java/NumPy，请务必把内层循环对应最右边的下标。

第四部分：数组越界与缓冲区溢出——危险的游戏

1. 数组本身没有“边界感”

在 Python 或 Java 中，如果你写 arr[10] 但数组只有 5 个元素，程序会立刻报错 IndexError 或 ArrayIndexOutOfBoundsException。

你会觉得这是理所当然的。但在计算机底层（C语言/汇编语言）看来，这简直是多管闲事。

还记得那个寻址公式吗？

$Address = Base\_Address + (Index \times Size)$

关键点： 这个公式只是单纯的数学计算。

  • 如果你有一个长度为 3 的数组，基地址在 1000。

  • 你想访问下标 100 的元素。

  • 计算机底层会毫不犹豫地计算：$1000 + 100 \times 4 = 1400$。

  • 然后，CPU 会直接伸出手去抓地址 1400 的数据。

CPU 根本不关心、也不知道那个数组只有 3 个元素长。 它只负责执行指令。

这就像你住酒店，定的是 101 号房。但你拿了一把万能钥匙（指针），非要去开 105 号房的门。如果酒店保安（编译器/运行时环境）不拦着你，你就能进去。

2. 读取越界：看到了不该看的东西

如果你运气好，访问越界也许只是读到了一些乱码。 但在极端情况下，这会导致信息泄露（Heartbleed 漏洞）。

著名的 Heartbleed（心脏滴血） 漏洞，本质上就是利用了数组（缓冲区）读取越界。

  • 黑客对服务器说：“我发给你单词 'BIRD'（4个字母），请你把这个单词原样回传给我。”

  • 黑客实际发出的指令是：“这是 'BIRD'，但我要你回传 64KB 的数据。”

  • 服务器单纯地运用了数组逻辑，从 'BIRD' 所在的内存地址开始，往后读取了 64KB 的连续内存。

  • 这 64KB 的内存里，可能刚好存着别人的密码、私钥、信用卡号。

  • 服务器把这些机密数据一股脑发给了黑客。

3. 写入越界：缓冲区溢出攻击（Buffer Overflow）

读取只是泄密，写入越界（Overwrite）则能控制计算机。

为了理解这一点，我们需要稍微了解一下栈内存（Stack Memory）的结构。当程序运行一个函数时，数据在内存里是这样紧挨着排放的：

内存地址（从低到高）存放内容作用
0x100 - 0x107char buffer[8]你的局部数组变量
0x108 - 0x10B其他变量函数里的其他整数
0x10C - 0x10F返回地址 (Return Address)这就是命门！

什么是“返回地址”？ 当函数执行完后，CPU 需要知道下一步该去哪里继续执行代码。这个“下一步的地址”就保存在栈上，紧紧贴着你的局部变量数组。

攻击演示：

假设你的代码里有一个只能装 8 个字符的数组 buffer[8]，用来存用户名。

  1. 正常情况： 用户输入 "User"（4个字）。它乖乖地待在 0x100 到 0x103。一切正常。

  2. 攻击开始： 黑客输入了一串精心设计的、超长的字符串，由 20 个字符组成。

  3. 覆盖发生：

    • 前 8 个字符填满了 buffer。

    • 第 9-12 个字符覆盖了“其他变量”。

    • 第 13-16 个字符覆盖了“返回地址”！

黑客会把那个“返回地址”改写成一段恶意代码的内存地址。

  1. 夺取控制权： 当这个函数执行完毕，CPU 说：“好了，我该回家了，让我看看返回地址是多少。” 它读取了被篡改的地址，跳转了过去。 从此，程序不再按原计划运行，而是开始执行黑客注入的恶意代码（比如开启一个后门）。

这就是为什么 C/C++ 里的 strcpy (字符串复制) 函数被认为是极其危险的，因为它不检查数组边界。

4. 现代语言的“保镖”：性能的权衡

既然越界这么危险，为什么不修好它？

其实，现代语言（Python, Java, Go, Rust）都已经修好了。 它们引入了边界检查（Bounds Checking）。

在这些语言底层，每次你访问 arr[i] 时，代码实际上变成了这样：

// 伪代码：Python/Java 底层逻辑
if (i < 0 || i >= arr.length) {
    throw new IndexError("越界啦！");
}
return memory[base + i * size];

代价是什么？ 性能损耗。 每一次数组访问，都要多做一次 if 判断。

  • 在一个循环 1 亿次的图像处理算法中，这意味着多做 1 亿次比较运算。

  • 这就是为什么在极度追求性能的领域（操作系统内核、3A游戏引擎、高频交易），程序员依然偏爱 C/C++。他们宁愿承担风险，也要省去那个 if 判断，换取极致的速度。

第四部分总结

从底层安全角度看：

  1. 裸奔的数组： 在最底层，数组没有任何防护，越界访问是自由的，也是致命的。

  2. 栈溢出： 数组越界不仅仅是数据错乱，它能覆盖程序的控制流（Return Address），让黑客接管电脑。

  3. 安全 vs 速度： 高级语言帮你挡住了子弹（IndexError），但也拿走了你奔跑的一点点速度。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值