标准化流NF公式推导与讲解

1. 为什么需要标准化流

深度学习很多任务本质是学习复杂分布（probability distribution），例如：

生成模型：学习真实图片分布

概率推断：计算似然 p(x)

采样：从 p(x)生成新的样本

困难：

1.真实分布 p(x) 复杂，直接建模难。

2.生成模型（VAE、GAN、Diffusion）通常无法直接计算精确似然 p(x)。

核心想法：

我们不直接建模复杂分布，而是：

从一个简单分布（如高斯分布 pz(z)）采样

通过一个可逆的神经网络变换 ​ 把简单分布变换到复杂分布

这就是标准化流：

像我们熟悉的 GAN (生成对抗网络) 或者 VAE (变分自编码器) 都是实现这个目标的流行方法。而标准化流则从一个非常独特的角度切入，它基于一个经典的数学原理：变量替换公式 (Change of Variables Formula)。

我们不去直接对复杂的目标分布 pX​(x) 建模，而是从一个简单的基础分布 pZ​(z) （比如标准正态分布）出发，然后学习一个映射函数 x=f(z)，这个函数可以将从 pZ​(z) 中采样的点 z 变换成符合目标分布 pX​(x) 的点 x。

用一系列可逆且可计算Jacobian行列式的变换，把一个简单分布“流”到一个复杂分布。

2. 数学公式推导

简单讲解一下雅可比行列式：

假设你有一个函数 x=2z。这个函数把整条数轴拉长了两倍。

现在，在 z 的数轴上，区间 [4,5] 的长度是 1。经过 x=2z 变换后，它变成了 x 数轴上的区间 [8,10]，长度是 2。

如果把概率想象成撒在数轴上的一层沙子。原来在 [4,5] 区间的沙子，现在被摊薄了，铺在了长度是原来两倍的 [8,10] 区间里。为了保证沙子的总量不变（总概率为1），新区间里沙子的密度（概率密度）就必须变成原来的一半。

这个“一半”，就是校正因子。在微积分里，这个拉伸比例就是导数 2。而我们需要的密度校正因子就是1/2​。

雅可比行列式，就是这个“拉伸/压缩校正因子”在高维空间里的推广。 它告诉你，在 z 点附近的一小块“体积”，在经过函数 f 变换到 x 点附近后，被拉伸或压缩了多少倍。我们用它来校正概率密度，确保概率守恒。

Jacobian矩阵描述的是“小变化怎么被放大或压缩”。

假设：

潜变量 （例如标准正态分布 ）

观测变量 （神经网络变换）

f 可逆，逆函数

一维情况（最简单）：

假设 x=f(z)，而且 f可逆

那么

由概率守恒公式：

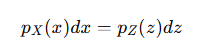
但

所以：

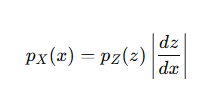
再写成log形式：

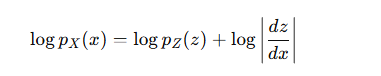
这个就是公式的雏形。

多维情况:

如果 x,z 是向量，则体积变化由 Jacobian矩阵 描述：

微小体积变化：

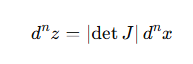
同样概率守恒：

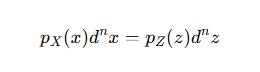
最后：

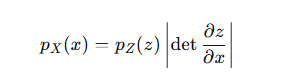
根据概率密度的变量变换公式：

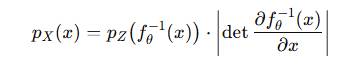
为了方便计算，我们通常使用对数形式，因为对数似然更容易优化：

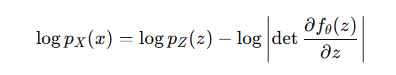
pX​(x) 是我们想求的，数据点 x 在目标分布中的概率密度。

det(⋅) 代表行列式。

：是逆函数 f^-1 关于 x 的雅可比矩阵 (Jacobian Matrix)，它描述了当 x 发生微小变化时，z 是如何相应变化的。

3. 多层流（Flow）

单层变换能力有限，所以我们用多层叠加,串联多个变换。

我们可以设计一系列相对简单但可逆的变换 f1​,f2​,…,fK​。我们让原始的简单分布像水流一样，依次穿过这些变换：

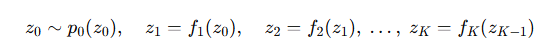
最终输出 。

这个由多个连续变换构成的序列，就被形象地称为“流” (Flow)。最终的变换函数 f=fK​∘⋯∘f2​∘f1​ 也是可逆的，它的雅可比行列式根据链式法则，等于每个变换的雅可比行列式的乘积。

在对数空间里，这就变成了一个非常优美的加法：

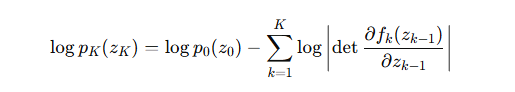
这个公式就是我们训练标准化流模型的目标函数。我们通过最大化训练数据在这个模型下的对数似然，来学习所有变换函数 f1​,…,fK​ 中的参数。

4. 关键设计：如何保证可逆+高效Jacobian

深度学习的网络通常很复杂，直接计算Jacobian行列式成本极高( O(n^3))。
NF的核心创新是特殊结构的变换，既能表示复杂分布，又能高效计算行列式。

一个非常巧妙的设计叫做耦合层 (Coupling Layers)，代表作有 RealNVP, NICE, Glow 等模型。它的思想如下：

假设输入向量 ，把它拆成两部分：

x_a：保持不变

x_b：被变换，但变换参数由 ​ 决定

输出：

s(⋅)：scale 网络（任意神经网络）

t(⋅)：translate 网络（任意神经网络）

⊙：逐元素乘法

Jacobian矩阵：

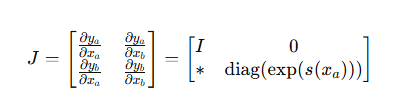
是下三角矩阵，
所以

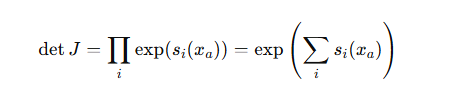
直接相加即可，无需复杂求解

因为 ​ 不变，
逆变换非常简单：

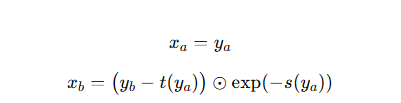
逆向计算只需一次前向网络。

Coupling Layer = 一半输入不动 + 用它去变另一半
这种设计让：

逆变换一步就能解（可逆性）

Jacobian行列式只需加法（效率）

多层交替后足够强大（表达力）

理解了这个套路，你就能照着搭 RealNVP、Glow 等标准化流的主干架构。

5.训练过程

Normalizing Flow（NF）的训练目标其实非常“干净”——
它不像 GAN 需要对抗，也不像 VAE 需要下界近似，
它直接就是最大似然估计（Maximum Likelihood Estimation, MLE）。

简单来说，训练的目标就是：调整我这一系列的可逆变换函数 f1​,f2​,…,fK​，使得我真实的训练数据，在经过这些函数变换后，看起来“最像是”从那个简单的基础分布（比如标准高斯分布）中采样出来的。

1. 训练目标：最大化真实数据的对数似然

我们有：真实数据分布：（只给样本，不给公式）

模型分布：（NF 定义的分布，参数 θ）

即：从你的训练数据集（比如一大堆人脸图片）中，随机抽取一个样本 x。

目标：

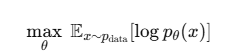
让 NF 模型分布 在训练数据上密度越大越好→ 让模型“生成”的分布尽可能贴近真实数据。

2. NF 的对数似然公式

因为 NF 定义了一个可逆映射 ，起始分布 pZ(z)（通常是标准高斯）已知，

所以可以精确写出 ：

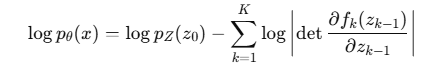
第一项：样本对应的 z0​ 在高斯下的对数概率。

第二项：所有变换的体积变化惩罚。

3. 前向与反向的关系

训练时给的是数据 x，
我们需要：

反向算 → 这一步必须可逆。

计算每层 Jacobian 的对角线或行列式（因为结构特殊，能高效算）。

带入公式算 。

4. 参数更新

损失函数：

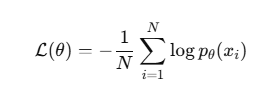
使用 梯度下降/Adam 直接优化。

NF 网络（Coupling Layer 的 s,t 网络、1x1 Conv 等）都能通过反向传播自动更新。

5. 训练流程（一个 batch）

1.采样数据：从真实数据集取 mini-batch {xi}。

2.逆映射：计算 。

3.Jacobian 行列式：计算每层 log det。

4.

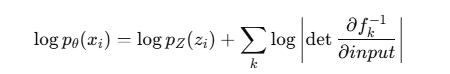
5.损失：取负平均 

6.反向传播 + 参数更新。