VQ-VAE 驾驭离散潜在空间：模型讲解与Pytorch代码解析

今天我们来学习一种非常强大且富有影响力的生成模型——向量化变分自编码器（Vector Quantised-Variational Autoencoder），简称 VQ-VAE。它巧妙地将连续的潜在空间与离散的表示结合起来，为高质量的图像、音频生成等任务打开了新的大门。

引言：为何需要离散表示？

在之前的章节中，我们学习了变分自编码器（VAE）。VAE 通过将输入数据编码到一个连续的、满足高斯分布的潜在空间 z 中，再从这个空间中采样并解码，从而实现数据的生成。这种连续的潜在空间非常强大，但也存在一些问题。

当解码器非常强大时，模型可能会忽略潜在变量 z ，直接从解码器中学习数据的分布，导致所谓的“后验坍塌”（Posterior Collapse）问题。

“后验坍塌”的发生过程：

首先，我们回忆一下VAE的目标是最大化证据下界（ELBO）：

ELBO = E[log p(x|z)] - KL[q(z|x) || p(z)]

现在，我们站在模型优化的角度，看它会如何“理性”地选择：

路径一：利用编码器-解码器通路

编码器需要努力工作，将输入 x的丰富信息压缩成一个有意义的分布 q(z|x)。
解码器需要学会解读这个 z，并准确地重构出 x。
这条路需要编码器和解码器精密配合，对模型来说有一定难度。

路径二：解码器“单干”

编码器“偷懒”了。它不再费心去从 x中提取有用信息，而是直接输出一个与先验分布 p(z)几乎一样的分布。也就是说，对于任何输入 x，q(z|x) ≈ p(z)。
此时，从编码器传到解码器的 z是一个几乎随机的噪声，不包含任何关于 x的信息。
但是！ 强大的解码器发现，即使拿到的是随机噪声，它也能依靠自己强大的能力生成一个看起来“像模像样”的样本（虽然不一定是精确的 x）。
同时，由于 q(z|x) ≈ p(z)，KL散度项会变得非常小，接近于0。这对于优化ELBO目标是一个非常“诱人”的收益。

模型的“理性选择”：

优化过程就像是一个精打细算的商人。它发现：

如果走路径一，重构损失可能会很低，但KL散度项会有一定的代价。
如果走路径二，重构损失可能不会降到最低，但KL散度项的巨大收益完全可以弥补重构损失上那一点点的劣势，从而使得总的ELBO目标值更优。

于是，模型自然而然地选择了路径二。这就是后验坍塌：对于所有输入 x，后验分布 q(z|x)都“坍塌”成了先验分布 p(z)。潜在变量 z失去了意义，因为它不再编码任何关于输入 x的信息。

一个比喻

一个学生（解码器）和一个助教（编码器）在完成作业：

任务：学生要根据助教的提示（z）来解答一道难题（x）。
正常情况：助教认真分析题目，给出关键提示（有信息的 z）；学生根据提示解题。
后验坍塌（强大学生）：学生是个天才，即使助教给的提示是“随便做就行”（无信息的 z），他也能靠自己强大的知识蒙个八九不离十。同时，因为助教给的提示很“通用”（接近先验），系统认为助教的工作很“规范”。久而久之，助教发现随便给提示反而整体评价更高，于是他就不再费心提供有用信息了。

此外，对于许多现实世界的数据，例如语言（由离散的单词组成）或图像中的物体（可以被归类为离散的类别），使用离散的表示可能比连续的向量更为自然和高效。

想象一下，如果我们的潜在空间不是一个连续的向量，而是一个从“字典”中查询到的“编码”，会怎么样？这个“字典”是有限的、离散的。这种想法正是 VQ-VAE 的核心。VQ-VAE 的目标是学习一个离散的潜在表示，同时保留自编码器强大的数据压缩和重建能力。

VQ-VAE 的核心思想：向量量化

VQ-VAE 的精髓在于其“向量量化”（Vector Quantisation, VQ）过程。让我们一步步拆解它的结构。

一个 VQ-VAE 模型主要由三部分组成：

1.编码器 (Encoder)：与标准的自编码器一样，编码器接收输入数据 x ，并将其映射到一个连续的潜在表示 ze(x)。

2.码本 (Codebook)：这是 VQ-VAE 的新组件。它是一个可学习的嵌入空间，我们可以将其想象成一本“密码本”或者“字典”。这个码本包含 K 个 D 维的向量，记为 e={e1,e2,…,eK}，其中每个 ei∈RD。

3.解码器 (Decoder)：接收量化后的潜在表示 zq(x)，并尝试重建原始输入 x^。

整个前向传播的过程是：

x ──Encoder──► z_e(x) ∈ R^{H×W×D}
                   │
                   │最近邻量化 NN
                   ▼
              z_q(x) = e_k ∈ R^{H×W×D}   (e_k 来自码本 E = {e_1,…,e_K})
                   │
                   └──Decoder──► x̂

Encoder：将输入 x 映射到连续潜特征 $z_e(x)$ ，通常带下采样（Stride/ResBlock）。

Vector Quantizer（量化器）：对每个位置的 $z_e$ 找到与码本中某个向量 $z_e$ 的最近邻（常用欧氏距离），输出离散代表 $z_q$ （但保持与 ze 相同维度）。

Decoder：条件于 zq 重构 x。

关键步骤：量化

量化的过程发生在编码器产生 ze(x) 之后。对于编码器输出的每一个向量，我们会在码本 e 中寻找与它“最接近”的那个码本向量。这个“接近”通常用欧氏距离来衡量。

具体来说，量化步骤如下：

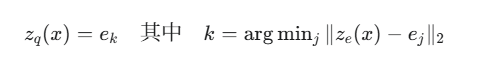
这里的 ze(x) 是编码器的输出，而 ej 是码本中的第 j 个向量。我们找到距离 ze(x) 最近的那个 ej 并将其作为量化后的向量 zq(x) 传递给解码器。这个过程就像查字典，将一个连续的、可能有些模糊的“意思”（ze(x)）映射到字典里最接近的那个标准“词条”（ek）。

我们很快就会发现一个大问题：argmin 这个操作是不可微分的。这意味着在进行反向传播时，梯度无法从解码器的输入 zq(x) 传递到编码器的输出 ze(x)。如果梯度流被中断，我们就无法训练编码器。

VQ-VAE 的作者们提出了一种非常聪明的解决方案：直通估计器 (Straight-Through Estimator, STE)。

它的工作原理如下：

前向传播时：我们正常执行量化操作，即 zq(x)=ek。

反向传播时：我们“假装”量化操作不存在，直接将解码器输入端的梯度 ∇zqL 复制给编码器的输出端。也就是说，我们令 ∇zeL=∇zqL。

这样，梯度就可以“跳过”不可导的量化步骤，直接传递给编码器，从而让整个模型能够通过梯度下降进行端到端的训练。

VQ-VAE 的损失函数

为了让编码器、解码器和码本这三者协同工作，VQ-VAE 设计了一个包含三个部分的精巧损失函数：

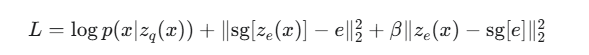
让我们逐一解析这三个部分：

：标准的重建损失。对于连续数据（如图像），它通常是均方误差 (MSE)

：码本损失，用于更新码本中的向量。这里的 sg 代表 stop-gradient（停止梯度）操作，意味着它的梯度不会回传给其输入 ze(x)。这个损失项的目的是将码本向量 e “拉向”编码器的输出 ze(x)。换句话说，它让我们的“字典”去主动学习数据中的常见模式。

：承诺损失，是一个正则化项。它与码本损失看起来很像，但 stop-gradient 的位置不同。这个损失项鼓励编码器的输出 ze(x) “承诺”于其选择的码本向量 e，不要离它太远。它防止编码器的输出空间无限增长，并确保编码器的输出能够稳定地映射到离散的码本上。β 是一个超参数，用于控制这项损失的权重，通常取值为 0.25 左右。

通过这三个损失项的共同作用，编码器学会了生成能够被码本很好地量化的表示，码本学会了捕捉数据中的关键特征，而解码器则学会了从这些离散的编码中重建高质量的数据。

作为生成模型：引入自回归先验

到目前为止，我们讨论的 VQ-VAE 还是一个自编码器，它可以对数据进行编码和解码，但还不能凭空生成新的数据。为了实现生成，我们需要学习离散潜在编码的分布 p(z)，我们称之为先验 (Prior)。

一旦 VQ-VAE 训练完成，它的编码器、解码器和码本就固定下来了。这时，我们可以执行以下步骤：

将我们所有的训练数据 x 通过训练好的编码器和量化器，得到一系列离散的码本索引（Indices）。对于一张图像，这可能是一个由整数组成的二维网格。

训练一个强大的自回归模型，比如 PixelCNN 或 Transformer，来学习这些离散索引的联合分布 p(z)。这个模型将学习到哪些编码组合是“有意义的”，哪些是“无意义的”。

当我们需要生成一个新样本时：

1.我们从训练好的自回归先验模型 p(z) 中采样，生成一个新的离散编码序列。

2.将这个编码序列转换回对应的码本向量 ek。

3.将这些向量送入 VQ-VAE 的解码器，生成一个全新的、前所未见的样本 x^。

这种将表示学习（VQ-VAE）和先验学习（自回归模型）解耦的策略是 VQ-VAE 能够生成高质量样本的关键。它允许我们分别使用最适合各自任务的模型。

VQ-VAE 及其变体已经在多个领域取得了巨大成功：

图像生成：VQ-VAE-2 和后续的 VQGAN、DALL-E 等模型能够生成极其逼真和多样化的高清图像。
音频合成：可用于高质量的文本到语音转换（TTS）和音乐生成。
视频生成：通过对视频帧进行离散编码，并学习编码序列的动态变化。
无监督表示学习：学习到的离散码本可以作为下游任务（如分类）的优质特征。

VQ-VAE 不仅仅是一个模型，更是一种思想：即在复杂的连续世界中，寻找一种简洁、离散且强大的表示方法。这一思想深刻地影响了后续许多先进生成模型的设计。

代码讲解

import torch, torch.nn as nn, torch.nn.functional as F

class VectorQuantizerEMA(nn.Module):
    def __init__(self, num_codes=1024, code_dim=256, decay=0.99, eps=1e-5, beta=0.25, use_ema=True):
        super().__init__()
        self.K, self.D = num_codes, code_dim
        self.beta = beta
        self.use_ema = use_ema
        self.register_buffer("embed", torch.randn(self.K, self.D))           # [K, D]
        self.register_buffer("cluster_size", torch.zeros(self.K))            # EMA N_k
        self.register_buffer("embed_avg", torch.randn(self.K, self.D))       # EMA m_k
        self.decay, self.eps = decay, eps

    def forward(self, z_e):  # z_e: [B, D, H, W]
        B, D, H, W = z_e.shape
        z = z_e.permute(0,2,3,1).contiguous().view(-1, D)  # [N, D], N=BHW

        # distances to codebook (||z - e||^2 = z^2 + e^2 - 2 z·e)
        z_sq = (z**2).sum(1, keepdim=True)              # [N,1]
        e_sq = (self.embed**2).sum(1)                   # [K]
        dist = z_sq + e_sq - 2 * z @ self.embed.t()     # [N,K]

        idx = torch.argmin(dist, dim=1)                 # [N]
        z_q = self.embed[idx].view(B, H, W, D).permute(0,3,1,2).contiguous()

        # commitment loss
        loss_commit = self.beta * F.mse_loss(z_e.detach(), z_q)

        if self.use_ema:
            # EMA updates (no grad)
            with torch.no_grad():
                onehot = F.one_hot(idx, self.K).type(z.dtype)  # [N,K]
                cluster_size = onehot.sum(0)                   # [K]
                embed_sum = onehot.t() @ z                     # [K,D]

                self.cluster_size.mul_(self.decay).add_(cluster_size, alpha=1-self.decay)
                self.embed_avg.mul_(self.decay).add_(embed_sum, alpha=1-self.decay)

                # Laplace smoothing to avoid zeros
                n = self.cluster_size.sum()
                cluster_size = (self.cluster_size + self.eps) / (n + self.K*self.eps) * n
                self.embed.copy_(self.embed_avg / cluster_size.unsqueeze(1))

            # straight-through: pass grad to z_e
            z_q = z_e + (z_q - z_e).detach()
            loss_codebook = torch.tensor(0., device=z_e.device)
        else:
            # original gradient-based codebook loss
            loss_codebook = F.mse_loss(z_e.detach(), z_q)
            z_q = z_e + (z_q - z_e).detach()

        # perplexity (code usage)
        with torch.no_grad():
            avg_probs = torch.zeros(self.K, device=z_e.device).scatter_add_(0, idx, torch.ones_like(idx, dtype=torch.float))
            avg_probs = avg_probs / avg_probs.sum().clamp_min(1)
            perplexity = torch.exp(-(avg_probs * (avg_probs.clamp_min(1e-10)).log()).sum())

        return z_q, loss_commit + loss_codebook, perplexity

class Encoder(nn.Module):
    def __init__(self, in_ch=3, hdim=128, zdim=256):
        super().__init__()
        self.net = nn.Sequential(
            nn.Conv2d(in_ch, hdim, 4, 2, 1), nn.ReLU(),
            nn.Conv2d(hdim, hdim, 4, 2, 1), nn.ReLU(),
            nn.Conv2d(hdim, zdim, 3, 1, 1)
        )
    def forward(self, x): return self.net(x)  # [B,zdim,H/4,W/4]

class Decoder(nn.Module):
    def __init__(self, out_ch=3, hdim=128, zdim=256):
        super().__init__()
        self.net = nn.Sequential(
            nn.Conv2d(zdim, hdim, 3, 1, 1), nn.ReLU(),
            nn.ConvTranspose2d(hdim, hdim, 4, 2, 1), nn.ReLU(),
            nn.ConvTranspose2d(hdim, out_ch, 4, 2, 1), nn.Sigmoid()
        )
    def forward(self, z_q): return self.net(z_q)

class VQVAE(nn.Module):
    def __init__(self, K=1024, D=256, use_ema=True):
        super().__init__()
        self.enc = Encoder(zdim=D)
        self.vq  = VectorQuantizerEMA(num_codes=K, code_dim=D, use_ema=use_ema)
        self.dec = Decoder(zdim=D)
    def forward(self, x):
        z_e = self.enc(x)
        z_q, vq_loss, ppl = self.vq(z_e)
        x_hat = self.dec(z_q)
        rec_loss = F.l1_loss(x_hat, x)
        loss = rec_loss + vq_loss
        return x_hat, loss, {"rec": rec_loss.item(), "ppl": ppl.item()}

1. `VQVAE` (整体模型)

我们先从顶层模型 VQVAE 开始：

class VQVAE(nn.Module):
    def __init__(self, K=1024, D=256, use_ema=True):
        super().__init__()
        self.enc = Encoder(zdim=D)
        self.vq  = VectorQuantizerEMA(num_codes=K, code_dim=D, use_ema=use_ema)
        self.dec = Decoder(zdim=D)

    def forward(self, x):
        z_e = self.enc(x)
        z_q, vq_loss, ppl = self.vq(z_e)
        x_hat = self.dec(z_q)
        rec_loss = F.l1_loss(x_hat, x)
        loss = rec_loss + vq_loss
        return x_hat, loss, {"rec": rec_loss.item(), "ppl": ppl.item()}

__init__:

K=1024: 码本 (Codebook) 的大小，即“字典”里有 1024 个“单词”。
D=256: 码本中每个“单词”（嵌入向量）的维度。
它初始化了三个子模块：一个编码器 self.enc、一个向量量化层 self.vq 和一个解码器 self.dec。

forward:

z_e = self.enc(x): 输入图像 x 被编码器压缩成一个连续的潜在表示 z_e。
z_q, vq_loss, ppl = self.vq(z_e): 关键的量化步骤。连续的 z_e 被量化为离散的 z_q。这一步同时计算出量化相关的损失 vq_loss 和一个衡量码本使用情况的指标“困惑度” ppl。
x_hat = self.dec(z_q): 解码器接收离散的 z_q，并尝试重建出原始图像 x_hat。
rec_loss = F.l1_loss(x_hat, x): 计算重建图像和原始图像之间的 L1 损失（也可以用 MSE/L2 损失）。这是重建损失。
loss = rec_loss + vq_loss: 模型的总损失是重建损失和 VQ 损失之和。这个总损失用于通过反向传播来训练整个模型。

2. `Encoder` 和 `Decoder` (编码与解码)

这两个模块是标准的卷积神经网络结构。

class Encoder(nn.Module):
    def __init__(self, in_ch=3, hdim=128, zdim=256):
        super().__init__()
        self.net = nn.Sequential(
            nn.Conv2d(in_ch, hdim, 4, 2, 1), nn.ReLU(),
            nn.Conv2d(hdim, hdim, 4, 2, 1), nn.ReLU(),
            nn.Conv2d(hdim, zdim, 3, 1, 1)
        )
    def forward(self, x): return self.net(x)  # [B,zdim,H/4,W/4]

它的作用是降维和特征提取。通过两个步长为 2 的卷积层，它将输入图像的空间尺寸（高度 H 和宽度 W）缩小为原来的 1/4，同时将通道数从输入通道 in_ch (例如彩色图为 3) 变为潜在维度 zdim (D=256)。输出 z_e 是一个特征图。

class Decoder(nn.Module):
    def __init__(self, out_ch=3, hdim=128, zdim=256):
        super().__init__()
        self.net = nn.Sequential(
            nn.Conv2d(zdim, hdim, 3, 1, 1), nn.ReLU(),
            nn.ConvTranspose2d(hdim, hdim, 4, 2, 1), nn.ReLU(),
            nn.ConvTranspose2d(hdim, out_ch, 4, 2, 1), nn.Sigmoid()
        )
    def forward(self, z_q): return self.net(z_q)

它的作用是升维和图像重建，结构与编码器相反。它使用转置卷积 (ConvTranspose2d) 将量化后的特征图 z_q 的空间尺寸放大回原始图像大小，并将通道数恢复为 out_ch。最后的 Sigmoid 函数将输出值归一化到 (0, 1) 范围内，这适用于像素值在 [0, 1] 区间的图像。

3. `VectorQuantizerEMA` (核心：向量量化层)

class VectorQuantizerEMA(nn.Module):
    def __init__(self, num_codes=1024, code_dim=256, decay=0.99, eps=1e-5, beta=0.25, use_ema=True):
        super().__init__()
        self.K, self.D = num_codes, code_dim
        self.beta = beta
        self.use_ema = use_ema
        self.register_buffer("embed", torch.randn(self.K, self.D))           # [K, D]
        self.register_buffer("cluster_size", torch.zeros(self.K))            # EMA N_k
        self.register_buffer("embed_avg", torch.randn(self.K, self.D))       # EMA m_k
        self.decay, self.eps = decay, eps

__init__:

初始化码本 embed，它是一个形状为 [K, D] 的张量，即 [1024, 256]。register_buffer 意味着这个张量是模型状态的一部分（会随模型一起保存和加载），但不是一个需要梯度下降优化的参数。
use_ema=True: 这是一个重要的开关。它决定了码本是使用更稳定的指数移动平均 (EMA) 方式更新，还是使用原始论文中的梯度下降方式更新。EMA 通常是更好的选择。
cluster_size 和 embed_avg: 这两个是 EMA 更新时需要的辅助变量，分别用于追踪每个码本向量被使用的频率和分配给它的编码器输出向量的总和。

def forward(self, z_e):  # z_e: [B, D, H, W]
        B, D, H, W = z_e.shape
        z = z_e.permute(0,2,3,1).contiguous().view(-1, D)  # [N, D], N=BHW

        # distances to codebook (||z - e||^2 = z^2 + e^2 - 2 z·e)
        z_sq = (z**2).sum(1, keepdim=True)              # [N,1]
        e_sq = (self.embed**2).sum(1)                   # [K]
        dist = z_sq + e_sq - 2 * z @ self.embed.t()     # [N,K]

        idx = torch.argmin(dist, dim=1)                 # [N]
        z_q = self.embed[idx].view(B, H, W, D).permute(0,3,1,2).contiguous()

        # commitment loss
        loss_commit = self.beta * F.mse_loss(z_e.detach(), z_q)

        if self.use_ema:
            # EMA updates (no grad)
            with torch.no_grad():
                onehot = F.one_hot(idx, self.K).type(z.dtype)  # [N,K]
                cluster_size = onehot.sum(0)                   # [K]
                embed_sum = onehot.t() @ z                     # [K,D]

                self.cluster_size.mul_(self.decay).add_(cluster_size, alpha=1-self.decay)
                self.embed_avg.mul_(self.decay).add_(embed_sum, alpha=1-self.decay)

                # Laplace smoothing to avoid zeros
                n = self.cluster_size.sum()
                cluster_size = (self.cluster_size + self.eps) / (n + self.K*self.eps) * n
                self.embed.copy_(self.embed_avg / cluster_size.unsqueeze(1))

            # straight-through: pass grad to z_e
            z_q = z_e + (z_q - z_e).detach()
            loss_codebook = torch.tensor(0., device=z_e.device)
        else:
            # original gradient-based codebook loss
            loss_codebook = F.mse_loss(z_e.detach(), z_q)
            z_q = z_e + (z_q - z_e).detach()

        # perplexity (code usage)
        with torch.no_grad():
            avg_probs = torch.zeros(self.K, device=z_e.device).scatter_add_(0, idx, torch.ones_like(idx, dtype=torch.float))
            avg_probs = avg_probs / avg_probs.sum().clamp_min(1)
            perplexity = torch.exp(-(avg_probs * (avg_probs.clamp_min(1e-10)).log()).sum())

        return z_q, loss_commit + loss_codebook, perplexity

z = z_e.permute(0,2,3,1).contiguous().view(-1, D)  # [N, D], N=BHW

编码器输出 z_e 的形状是 [批量大小, 通道数, 高, 宽]。为了对每个“像素”的特征向量（长度为 D）进行量化，代码首先将其变形为一个二维张量 [N, D]，其中 N=B×H×W 是向量的总数。

dist = z_sq + e_sq - 2 * z @ self.embed.t()

这里用了一个非常高效的技巧来计算每个输入向量 z 与码本中所有向量 e 之间的欧氏距离的平方。公式是 ∣z−e∣2=∣z∣2+∣e∣2−2z⋅e。这避免了使用循环，而是通过矩阵运算一次性计算出所有距离，得到一个 [N, K] 的距离矩阵。

idx = torch.argmin(dist, dim=1)
z_q = self.embed[idx].view(B, H, W, D).permute(0,3,1,2).contiguous()

torch.argmin 找到了每个输入向量距离最近的码本向量的索引。然后用这些索引从码本 self.embed 中取出对应的向量，形成量化后的 z_q，并将其形状恢复为 [B, D, H, W] 以便送入解码器。

EMA 更新码本 (当 use_ema=True): 这部分代码在 with torch.no_grad(): 块中，意味着这里的操作不涉及梯度计算，而是直接修改码本。

它首先统计每个码本向量被选用了多少次 (cluster_size)，以及所有映射到该码本向量的 z_e 向量之和 (embed_sum)。
然后使用 EMA 公式更新 self.cluster_size 和 self.embed_avg。
最后，新的码本向量通过 self.embed_avg / cluster_size 计算得出，即每个码本向量更新为其对应的所有 z_e 向量的移动平均值。这比用梯度下降更新更稳定，可以防止码本向量不被使用（所谓的 codebook collapse）。

损失计算与直通估计器 (STE):

Commitment Loss: loss_commit = self.beta * F.mse_loss(z_e.detach(), z_q)。这个损失项在 VQ-VAE 论文中用于鼓励编码器的输出 z_e 靠近它所选择的码本向量 z_q。注意：标准的 commitment loss 应该是 F.mse_loss(z_e, z_q.detach())，这样梯度只会更新编码器。此处的写法 z_e.detach() 是非标准的，它实际上会计算一个用于更新码本的梯度，这在 use_ema=False 时与 loss_codebook 作用类似。
Codebook Loss (当 use_ema=False): loss_codebook = F.mse_loss(z_e.detach(), z_q)。这是原始论文中提出的码本损失，它将码本向量拉向对应的编码器输出。