什么是标准化流?
想象一下,你有一块形状非常简单的橡皮泥,比如一个标准尺寸的立方体。通过一系列“可逆的”拉伸、挤压、扭曲操作,你可以把这块简单的橡皮泥变成任何你想要的复杂形状,比如一只猫。
标准化流(Normalizing Flows)在数学和机器学习中做的就是类似的事情,但处理的不是橡皮泥,而是概率分布。
核心思想:标准化流通过一系列可逆的(invertible)、可微分的(differentiable)函数变换,将一个简单的基础概率分布(比如标准正态分布,形状像一个标准的钟形曲线)转化成一个非常复杂的、我们想要建模的目标分布(比如所有猫的图像的像素分布)。
这个过程之所以强大,是因为每一步变换都是可逆的,并且我们能精确地计算出变换过程中概率密度是如何变化的。
为什么需要标准化流?
在机器学习,尤其是生成模型领域,我们经常想做两件核心的事情:
1.密度估计(Density Estimation):给定一个数据点(比如一张图片),计算它出现的概率有多大。这可以用来做异常检测(概率极低的点就是异常点)。
2.采样(Sampling):从我们学习到的数据分布中,生成新的、类似的数据点(比如生成一张全新的、不存在的猫的图片)。
很多生成模型(比如生成对抗网络 GANs 或变分自编码器 VAEs)在精确计算概率(密度估计)方面存在困难。而标准化流的核心优势就在于,它能精确地计算出任意数据点的概率,同时也能高效地生成新样本。
由于接下来的数学原理讲解需要用到雅可比矩阵,所以我先做个基础的雅可比矩阵讲解:
雅可比矩阵讲解
例如我们有一个机器(函数):
有多个输入入口(例如:温度、湿度、风速)
有多个输出出口(例如:体感温度、干燥指数、舒适度)
雅可比矩阵就是这个机器的灵敏度说明书,它告诉你:
每一个输出口对每一个输入口的微小变化有多敏感。
1.单输入单输出 (比如:油门深度 -> 车速):
导数d(车速)/d(油门)= 告诉你踩油门车速加多快。
这就是“一阶导数”,一个数就够了。
2.多输入单输出 (比如:油门深度 + 坡度 -> 车速):
梯度[∂(车速)/∂(油门), ∂(车速)/∂(坡度)]= 告诉你油门变化、坡度变化 各自 对车速的影响强度。
这就是“梯度”,一个(行)向量。
3.多输入多输出 (比如:油门深度 + 坡度 -> 车速 + 油耗):
这时需要一个表格,列出:
输出1(车速) 对 输入1(油门)的敏感度 ∂(车速)/∂(油门)
输出1(车速) 对 输入2(坡度)的敏感度 ∂(车速)/∂(坡度)
输出2(油耗) 对 输入1(油门)的敏感度 ∂(油耗)/∂(油门)
输出2(油耗) 对 输入2(坡度)的敏感度 ∂(油耗)/∂(坡度)
这个表格就是“雅可比矩阵” (两行两列)
关键作用:整体变化的精确描述
雅可比矩阵 J 就像一个放大镜,照在输入点的微小变化 Δx上,就能精确预测输出的微小变化 Δy:
[Δy₁] [ ∂y₁/∂x₁ ∂y₁/∂x₂ ... ∂y₁/∂xn ] [Δx₁]
[Δy₂] = [ ∂y₂/∂x₁ ∂y₂/∂x₂ ... ∂y₂/∂xn ] * [Δx₂]
[...] [... ... ... ... ] [...]
[Δyₘ] [ ∂yₘ/∂x₁ ∂yₘ/∂x₂ ... ∂yₘ/∂xn ] [Δxₙ]
\-----------------------------/
这就是雅可比矩阵 J
它让复杂的多输入多输出变化关系,变得可以精确计算!
举个简单的例子:机器人手臂关节运动
假设机器人小臂:
输入:肩膀转动角θ,手肘弯曲角φ(两个输入)。
输出:手腕的坐标(x, y)(两个输出)。
描述手腕位置与关节角的函数:
x = L₁ * cos(θ) + L₂ * cos(θ + φ) // L₁、L₂是臂长
y = L₁ * sin(θ) + L₂ * sin(θ + φ)
问:当肩膀角θ和手肘角φ微微变化时,手腕位置(x, y)会怎么动?怎么量化它们的关系?
解法:求雅可比矩阵
算 x 对 θ 的偏导 (J[1,1]): 求偏导数 ∂x/∂θ = -L₁*sin(θ) - L₂*sin(θ + φ)
算 x 对 φ 的偏导 (J[1,2]): ∂x/∂φ = -L₂*sin(θ + φ)
算 y 对 θ 的偏导 (J[2,1]): ∂y/∂θ = L₁*cos(θ) + L₂*cos(θ + φ)
算 y 对 φ 的偏导 (J[2,2]): ∂y/∂φ = L₂*cos(θ + φ)
雅可比矩阵 J 就是这么一张表:
| ∂x/∂θ ∂x/∂φ |
J = | |
| ∂y/∂θ ∂y/∂φ |
| -L₁*sin(θ) - L₂*sin(θ+φ) -L₂*sin(θ+φ) |
J = | |
| L₁*cos(θ) + L₂*cos(θ+φ) L₂*cos(θ+φ)|
它能做什么?
假设在某个姿势 (θ=60°, φ=45°)时,L₁=1, L₂=0.5,可以算出一个具体的 J:
| ∂x/∂θ ∂x/∂φ |
| -1 * sin(60) - 0.5*sin(105) -0.5*sin(105) |
| -1.366 -0.483 |
| ∂y/∂θ ∂y/∂φ |
| 1 * cos(60) + 0.5*cos(105) 0.5*cos(105) |
| 0.317 0.129 |
用途
如果肩膀角增加0.1弧度 (Δθ = 0.1),手肘角减少0.05弧度 (Δφ = -0.05):
[Δx] [ -1.366 -0.483 ] [ 0.1 ] [ (-1.366 * 0.1) + (-0.483*(-0.05)) ] [ -0.1366 + 0.02415 ] [ -0.11245 ] (约 -0.11)
[ ] = [ ] * [ ] = [ ] = [ ] ≈ [ ]
[Δy] [ 0.317 0.129 ] [-0.05] [ (0.317 * 0.1) + (0.129*(-0.05)) ] [ 0.0317 - 0.00645 ] [ 0.02525 ] (约 0.025)
预测手腕位置会:x方向左移约0.11单位,y方向上移约0.025单位。
找到最敏感的操作点
J矩阵中数值越大的位置(如这里的 ∂x/∂θ = -1.366,绝对值很大),说明 θ对 x位置影响非常敏感。
学会了雅可比矩阵,这下我们开始核心数学原理就简单了
核心数学原理:变量替换公式(Change of Variables Formula)
这是理解标准化流的关键。别被公式吓到,我们一步步解释。
假设我们有一个简单的随机变量 z,它的概率密度函数是 p_Z(z)。这个 z 来自我们的基础分布(比如标准正态分布),所以它的概率我们很容易计算。
现在,我们通过一个函数 f 把它变换成一个新的随机变量 x,即 x=f(z)。我们想知道 x 的概率密度函数 pX(x) 是什么。
变量替换公式告诉我们:
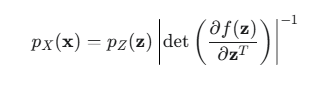
让我们拆解一下这个公式:
pX(x):这是我们最终想要的目标分布中,数据点 x 的概率密度。
pZ(z):这是基础分布中,对应点 z 的概率密度。因为 x=f(z),并且 f 是可逆的,所以我们可以通过 z=f^-1(x) 找到唯一的 z。
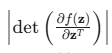 :这部分是关键,它叫做雅可比行列式(Jacobian Determinant)的绝对值。
:这部分是关键,它叫做雅可比行列式(Jacobian Determinant)的绝对值。
![]() :是雅可比矩阵,它衡量了函数 f 在点 z 附近引起的局部“体积”变化。想象一下,在 z 附近取一个微小的立方体,经过 f 变换后,它在 x 空间会变成一个微小的平行六面体。
:是雅可比矩阵,它衡量了函数 f 在点 z 附近引起的局部“体积”变化。想象一下,在 z 附近取一个微小的立方体,经过 f 变换后,它在 x 空间会变成一个微小的平行六面体。
这个矩阵的行列式(Determinant)就代表了这个“体积”变化的比例。如果行列式的值是 2,意味着体积被放大了 2 倍;如果是 0.5,意味着体积缩小了一半。
概率密度与体积成反比。如果一个区域的体积被拉伸扩大了,那么为了保持总概率为 1,该区域的概率密度就必须相应地降低。这就是为什么公式里是乘以行列式的倒数 |...|⁻¹。
标准化流的巧妙之处就在于,它构建的一系列变换函数 f,都满足两个条件:
1.可逆:我们可以轻松地从 x 计算回 z(f−1 容易计算)。
2.雅可比行列式易于计算:这是最重要的。如果雅可比矩阵是一个非常复杂的矩阵,计算它的行列式会非常耗时(通常是 O(D3),D是数据维度)。标准化流通过巧妙地设计函数结构(比如使用耦合层 Coupling Layers),使得雅可比矩阵变成一个三角矩阵。三角矩阵的行列式就是对角线上元素的乘积,计算起来非常快(O(D))。
在标准化流(Normalizing Flows)中,雅可比矩阵扮演着核心的角色——它不仅是模型可行的理论基础,更是实现概率密度变换的关键计算工具。以下从原理到实践逐步拆解其作用:
1. 标准化流的终极目标
核心问题:如何将一个简单的已知分布(如标准高斯分布 z∼N(0,I))通过一系列变换 f,映射为复杂的目标分布 px(x)?
核心要求:变换必须可逆,并且容易计算概率密度。
整个流程可以从两个方向看:
(1). 前向过程(Forward Pass / Inference):计算概率密度
这个过程用于密度估计。给定一个真实数据点 x,我们想计算它的概率 pX(x)。
1.逆向变换:我们从 x 出发,依次通过每个变换的逆运算,把它变回基础分布空间中的点 z0
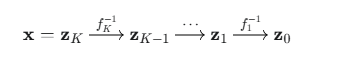
2.计算概率:利用变量替换公式的对数形式(log-likelihood),计算起来更稳定:
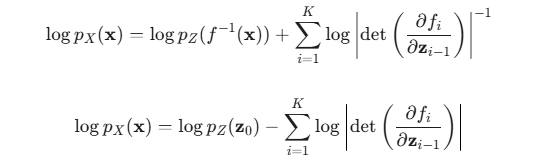
logpZ(z0):基础分布的对数概率,非常好算。
![]() :所有雅可比行列式的对数之和。因为每个变换 fi 都被设计成雅可比行列式易于计算,所以这部分也很好算。
:所有雅可比行列式的对数之和。因为每个变换 fi 都被设计成雅可比行列式易于计算,所以这部分也很好算。
训练模型:模型的目标就是最大化训练数据集中所有真实数据点的对数似然(log-likelihood)。通过反向传播算法,调整每个变换函数 fi 内部的参数(通常是神经网络的权重)即可。
(2). 反向过程(Backward Pass / Sampling):生成新样本
这个过程用于生成新数据。
1.从基础分布采样:随机从简单的高斯分布中抽取一个样本点 z0。
2.正向变换:将 z0 依次通过我们训练好的变换函数 f1,f2,…,fK,最终得到一个样本点 x
这个 x 就是一个来自模型学习到的复杂分布的全新样本。
2. 雅可比矩阵的三大核心作用
(1) 连接输入/输出分布的密度函数
通过 变量替换定理 (Change of Variables Formula):
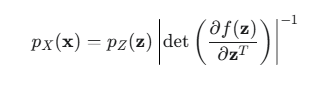
计算 px(x)只需计算 pz(z)并乘上 雅可比矩阵的行列式的绝对值的倒数。
(2) 约束变换的设计结构
标准化流要求:
可逆性:存在 f−1
行列式高效计算:det(Jf)必须在高维下快速求解
解决方案:设计特殊结构的雅可比矩阵
|
流模型类型 |
雅可比矩阵结构 |
行列式计算优化 |
|---|---|---|
|
NICE/RealNVP |
分块三角矩阵(如下图) |
det(J)=∏对角元 |
|
GLOW |
1x1 卷积 + 仿射耦合层 |
分解为小矩阵行列式乘积 |
|
Planar/Sylvester 流 |
低秩矩阵分解 |
用矩阵秩的性质简化计算 |
示例:RealNVP的分块三角雅可比矩阵
那么,如何设计一个既可逆、雅可比行列式又好算的变换呢?RealNVP(Real-valued Non-Volume Preserving)模型提出的耦合层是一个经典例子。
它的思想是“一部分不变,一部分变”:
1.将输入向量 z 分成两部分,za 和 zb。
2.第一部分 za 保持不变。
3.第二部分 zb 经过一个由 za 控制的、简单的仿射变换(缩放和平移)。
4.输出:
![]()
![]()
这里的 s (scale, 缩放) 和 t (translate, 平移) 是两个复杂的神经网络,它们的输入都是不变的那部分 za。
⊙ 表示逐元素相乘。
为什么这样设计?
可逆性:给定输出 x=(xa,xb),我们可以轻松地反解出输入 z=(za,zb)。
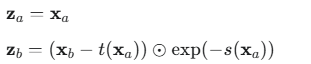
雅可比行列式:这个变换的雅可比矩阵是下三角矩阵(或上三角,取决于你如何排列):
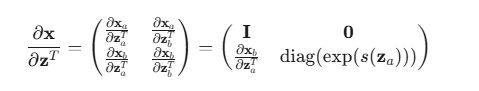
因为 xa=za,所以左上角是单位矩阵 I。
因为 xa 不依赖于 zb,所以右上角是零矩阵 0。
因为 xb 对 zb 的导数只在对角线有值,所以右下角是对角矩阵。
这个三角矩阵的行列式就是对角线元素的乘积,即
![]()
计算这个行列式只需要把神经网络 s 的输出向量加起来再取指数就行了,非常高效!
为了让所有维度都能变化,我们可以在不同的层之间交替分割的维度(例如,第一层保持前一半不变,第二层保持后一半不变)。
(3) 引导概率路径的“流动”方向
雅可比行列式 det(Jf)的符号和大小控制着分布变换的几何行为:
∣det(J)∣>1:局部概率密度被拉伸(如山峰被拉宽)
∣det(J)∣<1:局部概率密度被压缩(如低谷被填平)
反向传播:通过 log∣det(Jf)∣的梯度,模型学会“拉伸/压缩”空间以匹配目标分布
总结:标准化流中雅可比矩阵的不可替代性
|
角色 |
对应数学概念 |
实际意义 |
|---|---|---|
|
概率密度转换的标尺 |
det(J) |
量化局部空间的膨胀/收缩程度 |
|
模型结构设计的核心约束 |
矩阵稀疏性/三角化 |
实现高维可逆变换的高效计算 |
|
损失函数的直接组成部分 |
logdet项 |
反向传播引导模型拟合目标分布形状 |
简单说:没有高效计算的雅可比行列式,就没有标准化流!它让概率分布的复杂变换从理论走向工程实践。
我知道大家看到这里肯定也有懵逼的,我们马上进入一个超详细实践,完全搞懂标准化流:
实践:简单的一维 (1D) 例子
假设我们的目标是学习一个未知的、看起来有点奇怪的数据分布。我们收集到了一些数据点,它们似乎都集中在 4 的周围,但又不像一个标准的高斯分布。
我们的工具是一个标准化流模型,它包含:
1.一个简单的基础分布:我们选择标准正态分布 z∼N(0,1)。这个分布的中心在 0,方差是 1。
2.一个简单的可逆变换:我们使用一个仿射变换 (Affine Transformation),这是最简单的变换之一:
![]()
这里的 a 和 b 是模型的参数,我们需要通过学习来确定它们的值。为了保证 a 总是正数(这样变换就不会“翻转”空间,简化计算)
我们通常用 ![]() 来代替,其中 s 和 t 是我们要学习的参数。
来代替,其中 s 和 t 是我们要学习的参数。
我们先假设通过训练,模型学到了参数 s=1 和 t=4。
那么我们的变换函数就是:![]()
现在,我们来看看这个训练好的模型如何执行两个核心任务:密度估计和采样。
任务一:密度估计(计算一个点的概率)
假设我们观察到了一个新的数据点 x=5,我们想知道模型认为这个点出现的概率密度有多大,也就是计算 pX(5)。
根据我们之前讲的变量替换公式:
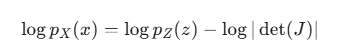
第 1 步:逆向变换,从 x 找到 z
我们需要先找到 x=5 在基础分布中对应的点 z 是什么
代入 x=5: z=(5−4)/e1=1/e≈0.368
所以,复杂分布中的点 x=5 对应于简单分布中的点 z≈0.368。
第 2 步:计算 z 在基础分布下的概率密度
我们的基础分布是标准正态分布,其概率密度函数是:
![]()
代入 z≈0.368:
pZ(0.368)=0.373
第 3 步:计算雅可比行列式
我们的变换是 f(z)=ez+4。这是一个一维函数,所以它的雅可比矩阵就是一个数字,也就是它的导数 f′(z)。
![]()
行列式就是它本身的值:det(J)=2.718。
第 4 步:组合起来,计算最终概率密度
现在我们可以计算 pX(5) 了:
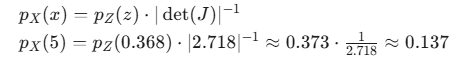
结论:我们的模型认为数据点 x=5 的概率密度大约是 0.137。在训练过程中,模型会调整参数 s 和 t,使得所有真实数据点的概率密度之和(对数似然)最大化。
直观理解: 我们的基础分布 N(0,1) 是一个以 0 为中心的钟形曲线。 我们的变换 f(z)=ez+4 做了两件事:
... * e^1:把整个分布“拉宽”了 e1≈2.718 倍。体积变大了,所以概率密度要除以 2.718。
... + 4:把拉宽后的分布从中心 0 平移到了中心 4。
所以,这个模型学习到的分布 pX(x) 是一个以 4 为中心,标准差为 e1≈2.718 的高斯分布,即
![]()
任务二:采样(生成一个新样本)
现在我们想让模型“画”一个新样本出来。这个过程就简单多了,是正向的。
第 1 步:从基础分布中采样一个 z
我们从标准正态分布 N(0,1) 中随机抽取一个点。假设我们抽到了 z=−0.5。
第 2 步:正向变换,从 z 生成 x
我们将这个 z 值代入我们的变换函数 f(z):
![]()
结论:我们成功生成了一个新的数据点 x=2.641。如果我们重复这个过程很多次,生成的这些点就会形成一个以 4 为中心的高斯分布,和我们上面分析的一样。
从简单例子到复杂应用
这个一维的例子非常简单,但它完美地展示了标准化流的核心机制。在真实应用中(比如图像生成),我们会:
1.处理高维数据:输入的 z 和输出的 x 都是高维向量(例如,一张 64x64 像素的图片就是一个 4096 维的向量)。
2.堆叠多个变换:只用一个简单的仿射变换能力有限。我们会把成百上千个更复杂的变换层(比如之前提到的 RealNVP 耦合层)串联起来:
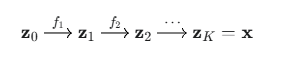
这样,一个非常简单的初始分布(高维高斯分布)就可以被逐步扭曲、拉伸,最终变成像人脸或猫的图像这样极其复杂的分布。
但无论模型多复杂,其底层的原理都和我们这个一维小例子是完全一样的:通过可逆变换和变量替换公式,在简单分布和复杂分布之间建立了一座精确的、可计算的桥梁。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








