溯源YOLOv1：单阶段目标检测的开山之作与数学原理超详细全解析

一、 核心思想：“把检测视为一个回归问题”

在YOLOv1之前，以R-CNN系列为代表的检测器都遵循一个两阶段（Two-Stage流程：

区域提议（Region Proposal）：先找出上千个可能包含物体的候选框。

分类与精修（Classification & Refinement）：再逐一判断这些候选框里是什么物体，并微调其位置。

这个过程非常缓慢。而YOLOv1的作者 Joseph Redmon 提出了一个了想法：我们为什么不直接在一个步骤里，同时预测出框的位置和类别呢？

YOLOv1的核心思想就是：将目标检测任务完全重新定义为一个单一的、端到端的回归问题（Regression Problem）。它对一张图片只看一次，就能直接回归出所有物体的边界框坐标和所属类别。

二、 架构原理

为了实现“看一次”就输出结果的目标，YOLOv1设计了一个简洁而巧妙的架构。

1. 网格系统 (The Grid System)
这是YOLOv1最核心、最基础的机制。

它将输入的图像统一缩放到 448x448 尺寸，然后逻辑上将其划分为一个 S x S 的网格（Grid），在论文中 S=7。

核心规则：如果一个物体的中心点（center）落入了某个网格单元（Grid Cell）内，那么这个网格单元就全权负责预测这一个物体。

这个规则是YOLOv1简洁性的来源，但也是其后续诸多局限性的根源。

2. 统一的网络结构
YOLOv1使用了一个单独的、统一的卷积神经网络（CNN）来完成所有工作。

灵感来源：其网络结构受到 GoogLeNet 的启发。

具体构成：它包含24个卷积层用于提取特征，以及2个全连接层用于进行最终的预测。没有复杂的组件，就是一路卷积到底，然后用全连接层输出一个大向量（张量）。

输出：网络的最终输出是一个形状为 S × S × (B × 5 + C) 的张量（Tensor）。这个张量包含了所有网格单元的预测信息。

三、 数学原理

这里的数学原理是课程的重点，我们将深入解析预测张量。

1. 预测张量 (The Prediction Tensor)

让我们来拆解这个 S × S × (B × 5 + C) 的输出张量。在YOLOv1论文中，S=7, B=2, C=20 (PASCAL VOC 数据集)，所以输出是 7 x 7 x 30 的张量。

我们聚焦于其中一个网格单元，它需要预测一个长度为 B × 5 + C（即30）的向量。这个向量包含三组信息：

A. 边界框预测 (B个，每个5个值)

每个网格单元会预测 B 个（比如2个）候选的边界框。每个边界框用5个值来描述：(x, y, w, h, confidence)。

(x, y)：预测框的中心点坐标。

注意：这个坐标是相对于其所在的网格单元的左上角进行归一化的，值在 [0, 1] 之间。例如，(0.5, 0.5) 表示中心点就在该网格单元的正中央。

(w, h)：预测框的宽度和高度。

注意：这个宽高是相对于整张图像的尺寸进行归一化的，值在 [0, 1] 之间。例如，(0.5, 0.5) 表示框的宽高都是整张图的一半。

confidence：置信度。这是一个非常重要的值，它代表了这个预测框的“质量”，其数学定义是：

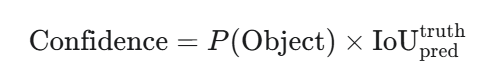
P(Object)：表示这个框内包含一个物体的概率。

IoU：是预测框（pred）与真实物体框（truth）之间的交并比。

直观理解：如果框内没有物体，P(Object)=0，则置信度为0。如果框内有物体，P(Object)=1，则置信度就等于预测框与真实框的IoU。所以，置信度既反映了框内是否有物体的信心，也反映了框的位置有多准。

B. 类别概率 (C个值)

每个网格单元还会预测一组条件类别概率 (Conditional Class Probabilities)：

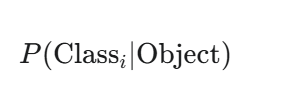
这表示，在“该网格单元内包含一个物体”这个前提条件下，这个物体属于第 i 个类别的概率。它一共有 C 个值，对应 C 个类别。

推理时的最终得分： 在进行预测时，我们将上述两组信息相乘，得到每个边界框对于每个类别的最终得分：

四，实例演示

理论知识需要一个实例来巩固。

我们来一起走一遍完整的流程，看看YOLOv1是如何处理一张真实图片的。

实例：检测一张包含“狗”和“自行车”的图片

假设我们有这样一张图片，左边有一只狗，右边有一辆自行车。

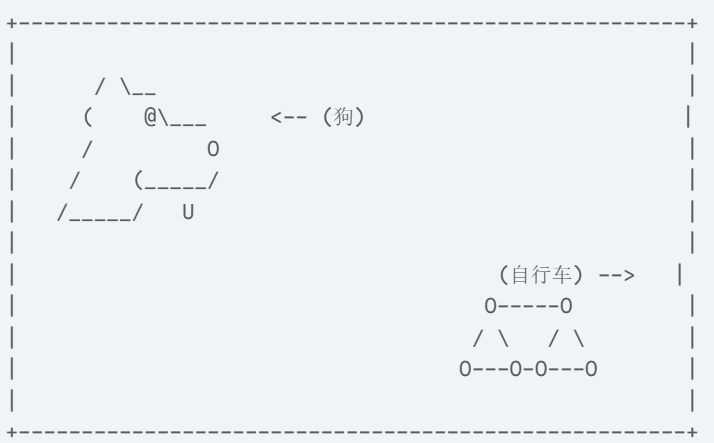
我们将使用YOLOv1的经典配置来进行分析：

输入尺寸：448 x 448

网格尺寸 (S)：7 x 7

每个单元格预测的边界框数 (B)：2

类别数 (C)：20 (假设“狗”是第12类，“自行车”是第2类)

第一步：图像预处理与网格划分

首先，YOLO将这张原始图片强制缩放到 448 x 448 像素。

然后，它在逻辑上将这张 448x448 的图划分成一个 7x7 的网格。

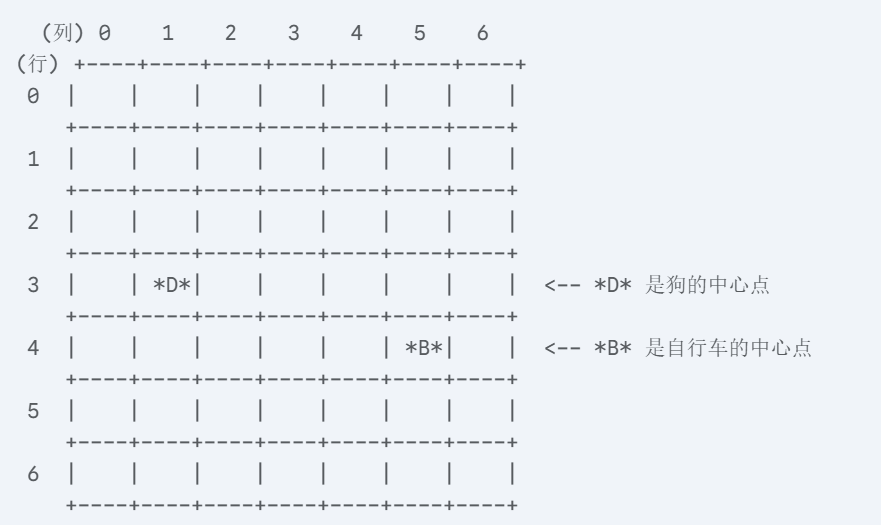
确定“负责”单元格：

狗的中心点落在了 (行=3, 列=1) 这个网格单元里。因此，(3, 1) 负责检测这只狗。

自行车的中心点落在了 (行=4, 列=5) 这个网格单元里。因此，(4, 5) 负责检测这辆自行车。

其他所有单元格，比如 (0, 0)，都是背景，不负责检测任何物体。

第二步：网络前向传播

这张 448x448 的图片被送入YOLOv1的CNN网络。经过24个卷积层和2个全连接层后，网络最终输出一个 7 x 7 x 30 的巨大张量。这个张量就是我们的预测结果。

第三步：解读预测张量 

现在，我们来“翻译”一下这个 7x7x30 张量里存储的信息。我们挑几个有代表性的单元格来看。

Case 1: 负责检测“狗”的单元格 (3, 1)：
这个单元格对应的 1x1x30 向量，在理想情况下，应该包含以下信息：

边界框1 (B1) 的5个值：假设这个框预测得很好。

x, y: (0.6, 0.7)  (狗的中心点在单元格偏右下角)

w, h: (0.30, 0.40) (狗的宽高约占整张图的30%和40%)

confidence: 0.95 (因为它框住了物体，且和真实框的IoU很高)

边界框2 (B2) 的5个值：这个框可能预测得不好。

x, y, w, h: (0.2, 0.3, 0.1, 0.1) (可能是任意值)

confidence: 0.05 (非常低的置信度，因为它没框住物体或IoU很低)

类别概率的20个值：

[0.01, 0.92, 0.01, ..., 0.98, ...] (第2类“自行车”的概率很低，第12类“狗”的概率非常高)

总的加起来就是30个数值正好对应30的维度了。

第四步：后处理 (得到最终结果)

网络输出的 7x7x2 = 98 个候选框还很原始，我们需要通过后处理来筛选出最终的结果。（因为每个网格会生成两个候选框，所以乘以2）

1.计算最终得分并进行阈值过滤：

对全部98个候选框，计算它们属于每个类别的最终得分：
Score(类别_i) = P(类别_i | Object) × confidence

例如，对于单元格(3,1)的B1框，它对“狗”的得分是 0.98 × 0.95 = 0.931。它对“自行车”的得分是 0.01 × 0.95 = 0.0095。

设定一个分数阈值（比如0.25）。所有类别的得分都低于这个阈值的框，全部被丢弃。

经过这一步，绝大多数来自背景区域的框和质量差的框都会被过滤掉。

2.非极大值抑制 (Non-Maximum Suppression, NMS)：

经过上一步过滤，可能还剩下一些高度重叠的框。例如，对于狗，可能有一个得分0.93的大框和一个得分0.85的稍微小一点的框。

NMS算法会解决这个问题：

a. 在剩余的框中，选择得分最高的那个框（比如0.93的狗的框），将它作为最终结果之一。

b. 计算其他所有框与这个最高分框的IoU。

c. 如果IoU超过一个阈值（比如0.5），就认为它们检测的是同一个物体，将这些低分框丢弃。

d. 从未被处理的框中，再次选择得分最高的，重复以上过程，直到所有框都被处理完毕。

最终输出：

经过NMS后，我们就得到了干净、唯一的检测结果：

一个围绕着狗的、类别为“狗”的边界框。

一个围绕着自行车的、类别为“自行车”的边界框。

这个例子将我们之前讨论的抽象数学原理、网络结构与一个直观的检测过程联系了起来。