【数据结构】AVL树原理及实现

一. AVL的概念

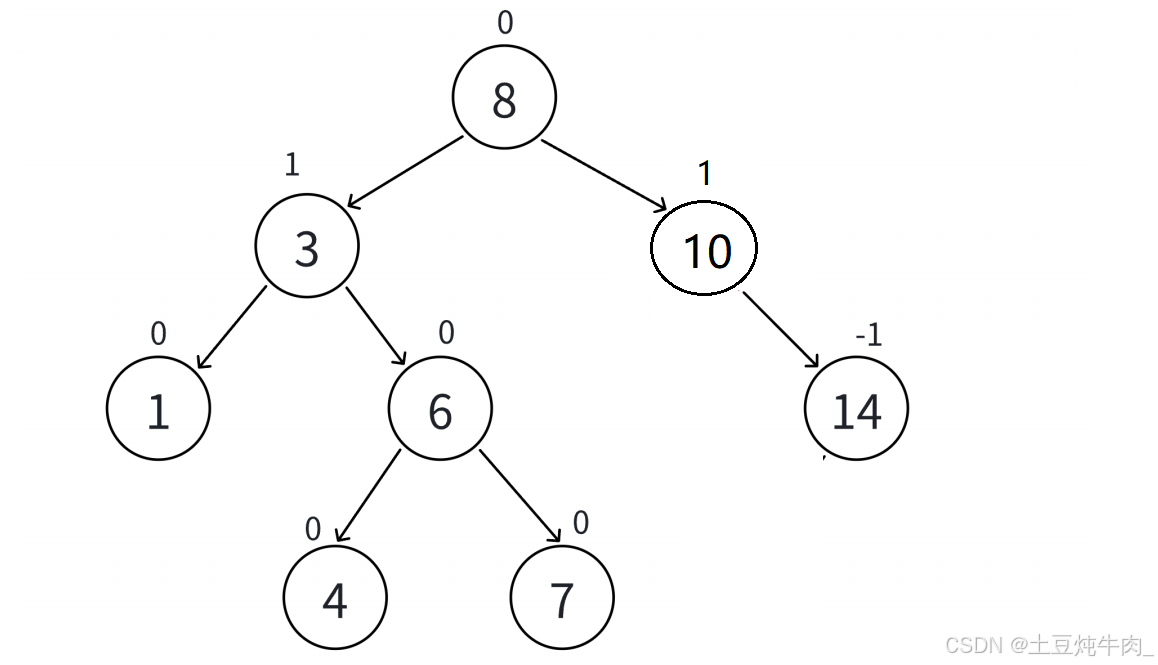
1. AVL树是一种自平衡二叉查找树，左右子树都是AVL树，左右子树的高度差不超过一，通过控制高度控制平衡
2. 这里可以在节点中引入一个平衡因子，通过平衡因子标记左右子树的高度差，平衡因子只能为0/1/-1，这样就方便观察和控制高度差
3. AVL树的节点分布和完全二叉树比较接近，高度可以控制在 logN，增删查改的效率就可以控制在logN，相比于二叉树有了很大提升

二. AVL树的实现

1.AVL树的结构

需要parent指针，方便平衡因子的调整

template <class K,class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V> _parent; ///需要parent指针，方便平衡因子的管理
	AVLTreeNode<K, V> _left;
	AVLTreeNode<K, V> _right;
	int _bf; ///balance factor

	AVLTreeNode(pair<K,V>&  kv)
		:_kv(kv)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
		,_bf(0)
	{}
};
template <class K, class V>
struct AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
     /// 
private:
	Node* _root = nullptr;
};

2.AVL树的插入

(1.) 插入的大概过程

1. 先按照二叉搜索树的规则进行插入
2. 更新平衡因子，节点的插入会影响父节点的平衡因子，要向上更新平衡因子
3. 如果更新平衡因子的过程中没有出现问题，插入结束
4. 如果插入过程中出现了不平衡，对不平衡的树进行旋转

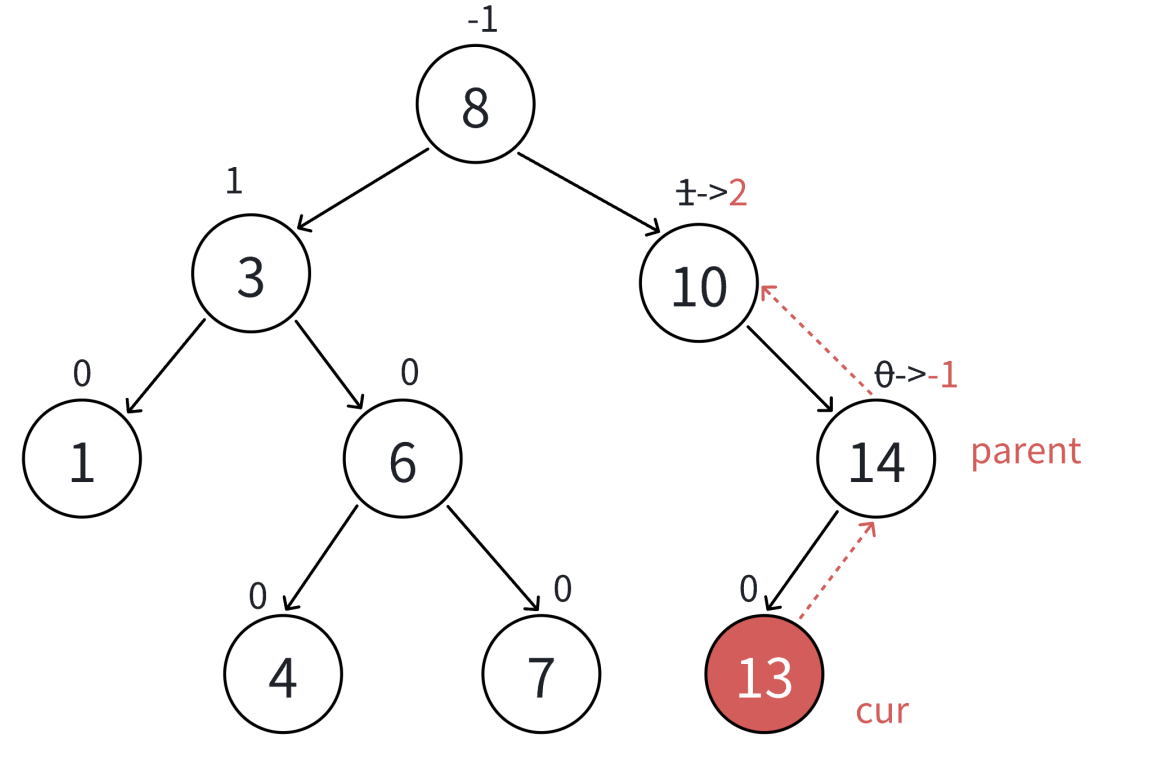
(2.)平衡因子更新

1. 平衡因子=右子树高度-左子树高度
2. 插入节点在parent节点的右边，parent的平衡因子++，反之–
3. 如果parent的平衡因子变成-1or1，说明原来是0，继续向上更新平衡因子；如果变成0，停止跟新，完成插入；如果变成2or-2,就要从当前parent的子树进行旋转
4. 如果更新到根节点还不到2or-2，插入成功
   

bool Insert(const T& data)
{
	//这里用_Insert函数执行二叉树的插入逻辑，如果返回空指针，代表元素已存在，不再插入
	Node* cur = _Insert(data);
	if (cur == nullptr)
		return false;
	//平衡因子的更新
	Node* parent = cur->_parent;
	while (parent)
	{
		if (cur == parent->_left)
			parent->_bf--;
		else
			parent->_bf++;
		//父节点平衡因子为零，插入结束，不用再调整了
		if (parent->_bf == 0)
			break;
		// 平衡因子变成1或-1，说明原来是0，需要向上继续调整
		 else if (parent->_bf == 1 || parent->_bf == -1)
		{
			cur = parent;
			parent = parent->_parent;
		}
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			//平衡因子变成2或-2，树已经不平衡了，需要翻转调整
		}
		else //平衡因子如果出现了其他的情况，说明代码逻辑错误
			assert(false);
	}
	return true;
}

(3.)旋转

旋转的原则

1. 保持树的特性
2. 是不平衡的书便平衡，降低树的高度
3. 一共有四种旋转，左单旋，右单旋，左右双旋，右左双旋

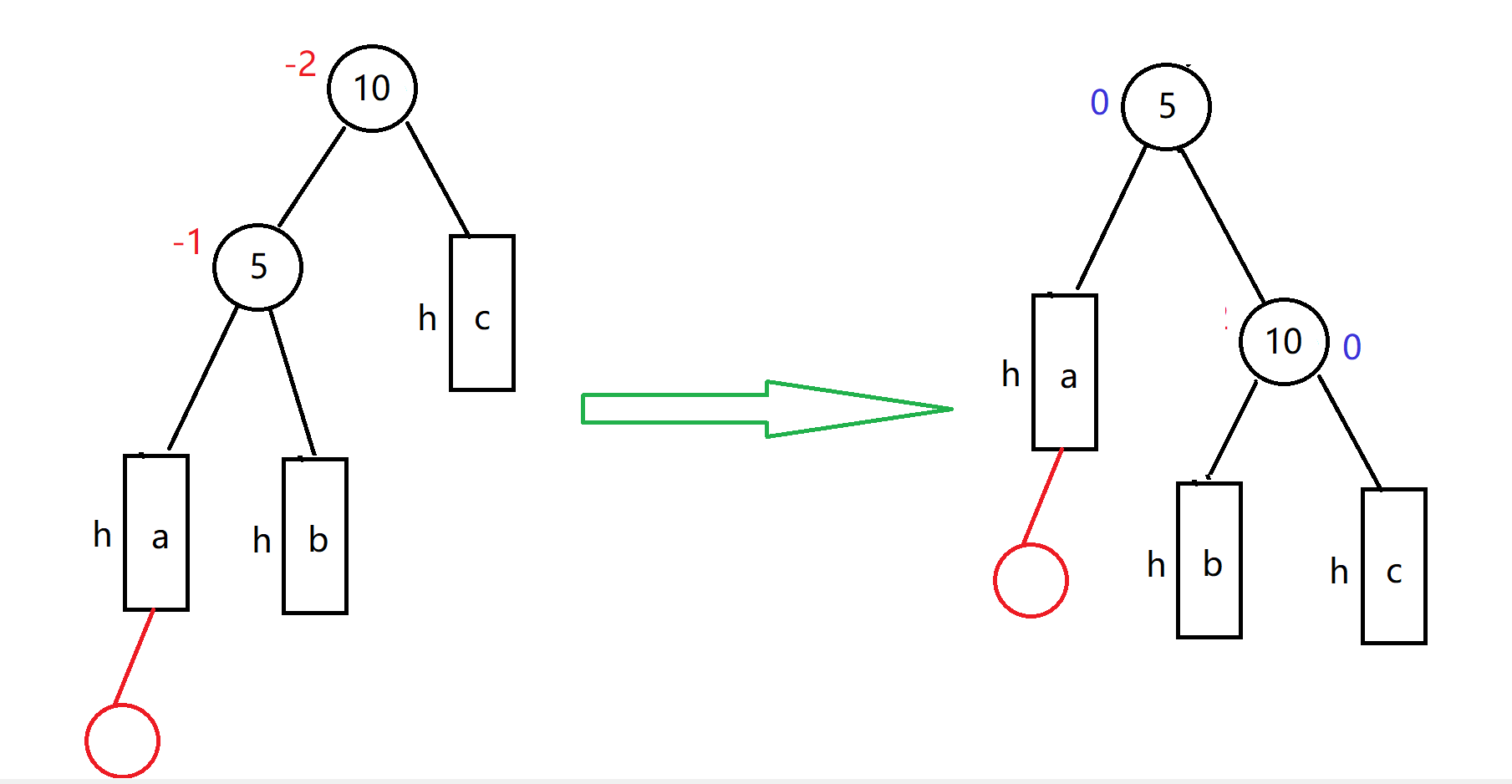
左单旋

使用场景：父节点平衡因子为-2，左子节点平衡因子为-1
原理：

1. 假设父结点的值为10，左子节点的值为5，a,b,c的高度都为h，a小于10，所以10及它的右树可以做5的右节点，b大于5同时又小于10，可以当10的左子节点
2. 旋转完之后更新原父节点和它的原左子节点的平衡因子，以及更新原左子节点的父子关系
   

void AVLTree<T> ::RorateR(AVLTreeNode<T>* root)
{
	typedef AVLTreeNode<T> Node;
	Node* parent = root;
	Node* subl = root->_left;
	//改变原父节点和左子节点的父子关系
	parent->_left = subl->_right;
	subl->_right = parent;
	Node* last_parent = parent->_parent;
	//如果原父节点的父节点为空，现父节点更新为根节点
	if (last_parent == nullptr)
	{
		subl = _root;
		subl->_parent = nullptr;
	}
	else
	{
		//判断原父节点位于它的父节点的左还是右
		if (last_parent->_left == parent)
			last_parent->_left = subl;
		else
			last_parent->_right = subl;
		subl->_parent = last_parent;
	}
	//更新平衡因子
	subl->_bf = parent->_bf = 0;
}

右单旋

使用场景：父节点平衡因子为2，右子节点平衡因子为1
原理同左单旋相同，代码也相似

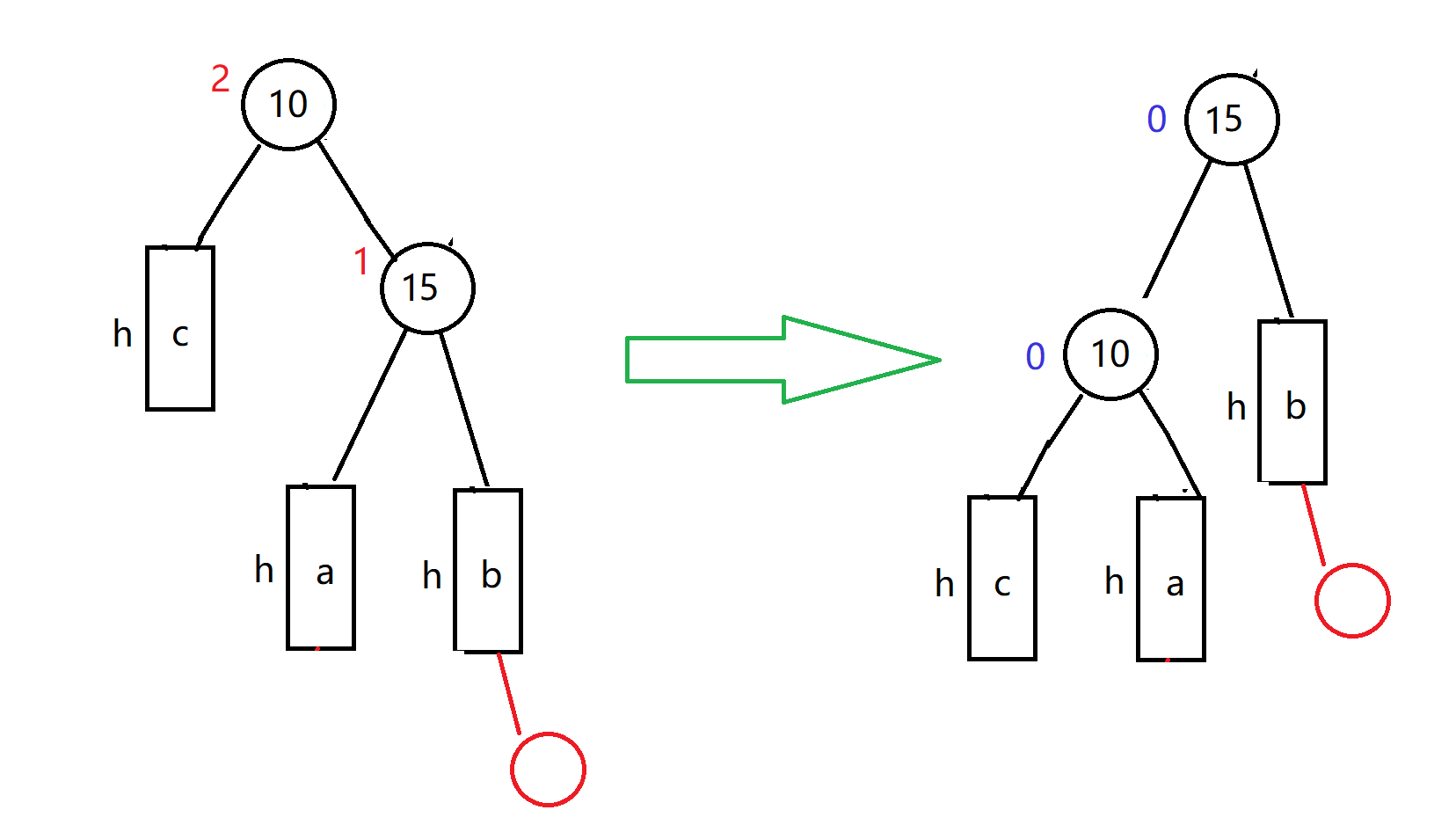
右左双旋

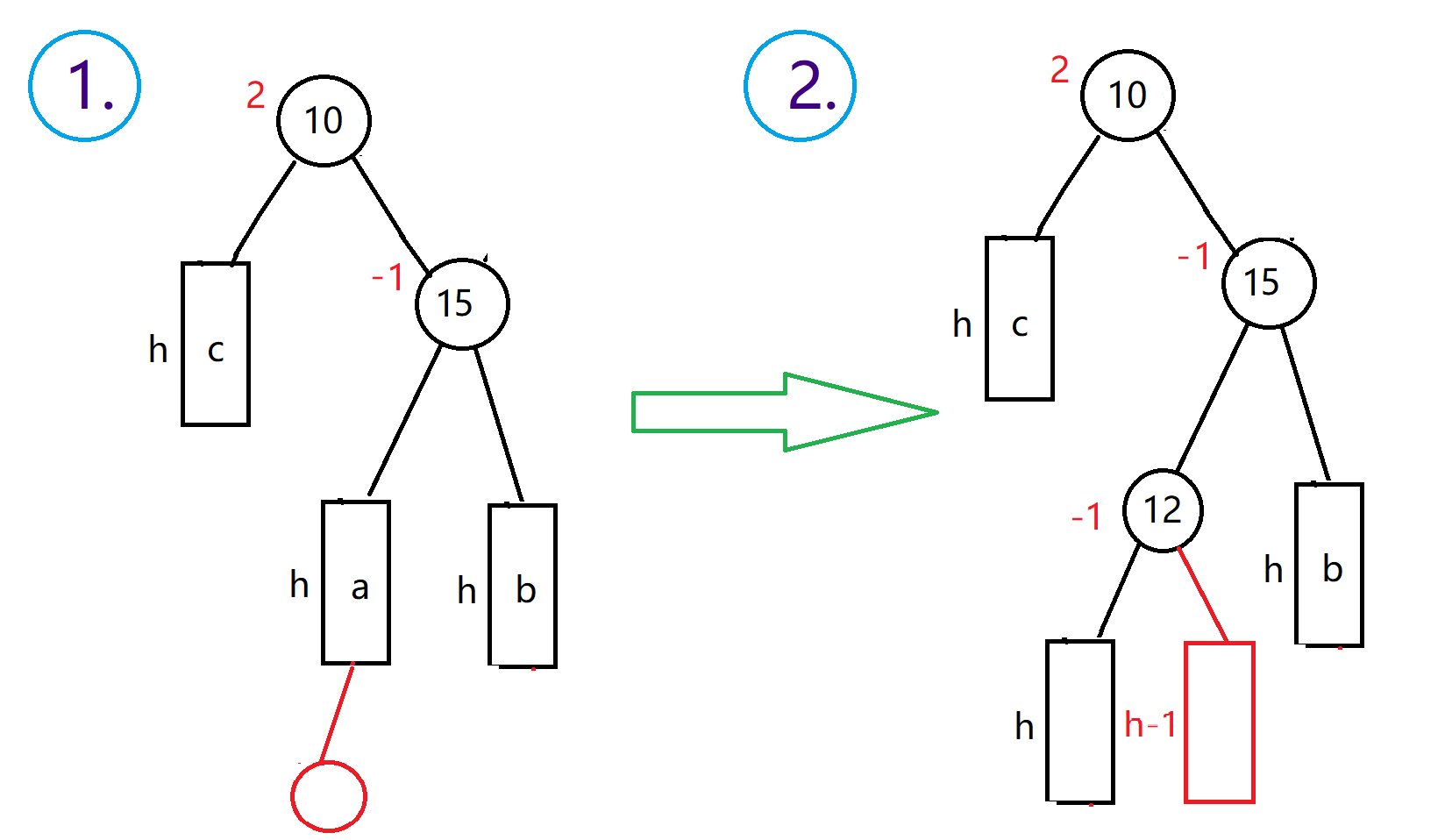
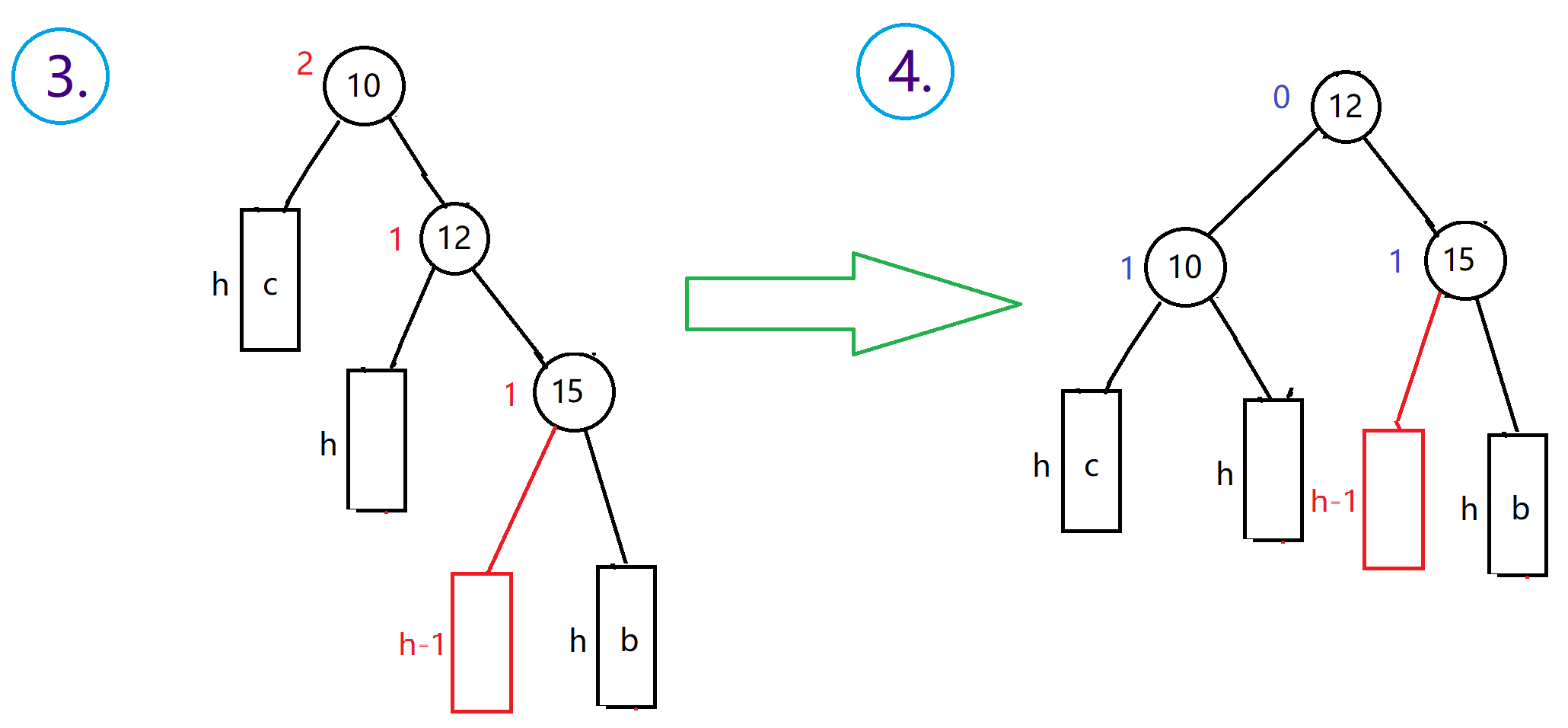
使用场景：父节点平衡因子为2，右子节点平衡因子为-1
过程：

1. 先对右子节点15的左子树进行拆分，15的左子树一定有一个小于15，假设是12，可拆分出12的左右子树
2. 然后对以15为父节点的树进行右旋转，得到一个符合左旋转条件的树，如图三
3. 最后对第一次旋转后的树进行第二次左旋转
4. 下图假设12的原始平衡因子是-1，但是12的平衡因子有三种情况1or-1or0,右左双旋完成后再根据具体情况改变10，12，15的平衡因子，具体看代码
   
   

template<class T>
void AVLTree<T> ::RorateRL(AVLTreeNode<T>* root)
{
	typedef AVLTreeNode<T> Node;
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int bf = subRL->_bf;
	RotateR(parent->_right); 
	RotateL(parent);
	if (bf == 0)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		parent->_bf = 0;
	}
	else if (bf == 1)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		parent->_bf = -1;
	}
	else if (bf == -1)
	{
		subR->_bf = 1;
		subRL->_bf = 0;
		parent->_bf = 0;
	}
	else
		assert(false);
}

左右双旋

使用场景：父节点平衡因子为-2，右子节点平衡因子为1
过程与右左双旋类似

(4.) 查找

查找就是二叉树查找，和插入逻辑一样

template<class T>
AVLTreeNode<T>* AVLTree<T> ::Find(T& key)
{
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (key > cur->_data)
		{
			parent = cur;
			cur = cur->_pRight;
		}
		else if (key < cur->_data)
		{
			parent = cur;
			cur = cur->_pLeft;
		}
		else
		{
			return cur;
		}
	}
	return nullptr;
}

(5.) 平衡检测

通过计算树的高度差是否合理并与平衡因子相同来判断，

template<class T>
size_t  AVLTree<T>::_Height(Node* root)
{
	if (root == nullptr)
		return 0;
	size_t leftHeight = _Height(root->_left);
	size_t rightHeight = _Height(root->_right);
	return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;
}
template<class T>
bool AVLTree<T>::_IsAVLTree(Node* root)
{
	if (root == nullptr)
		return true;
	_IsAVLTree(root->_left);
	_IsAVLTree(root->_right);
	size_t leftHeight = _Height(root->_left);
	size_t rightHeight = _Height(root->_right);
	size_t  balance = (rightHeight > leftHeight) ? (rightHeight - leftHeight) : (leftHeight - rightHeight);
	if (balance ==root->_bf)
		return true && _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
	else
		return false;
}