游戏中的AI---寻路算法A* [1]（上篇 Dijkstra算法铺垫）

0.简介

网上A*算法介绍已经很多很多了，不过我作为学习和实现，我还会把我的经历记录下来。

1.算法简介

A*算法，听到这个算法后，很难直接判断出这个算法是解决什么问题，这是解决寻路问题的，为什么叫A*？，据考证，最早是有A1,A2算法，后来发展了更优秀的算法就叫A*了，应该和B语言，C语言，C++的叫法类似吧。

2.算法详细介绍

现在进入正题，学习A*算法之前就先理解 一些迪杰斯特拉最短路径算法，首先简述一下Dijkstra算法流程。文字不太好叙述，画图的话用软件画比较不方便，所以我采用手画图，方便快捷。

图1 例子图1

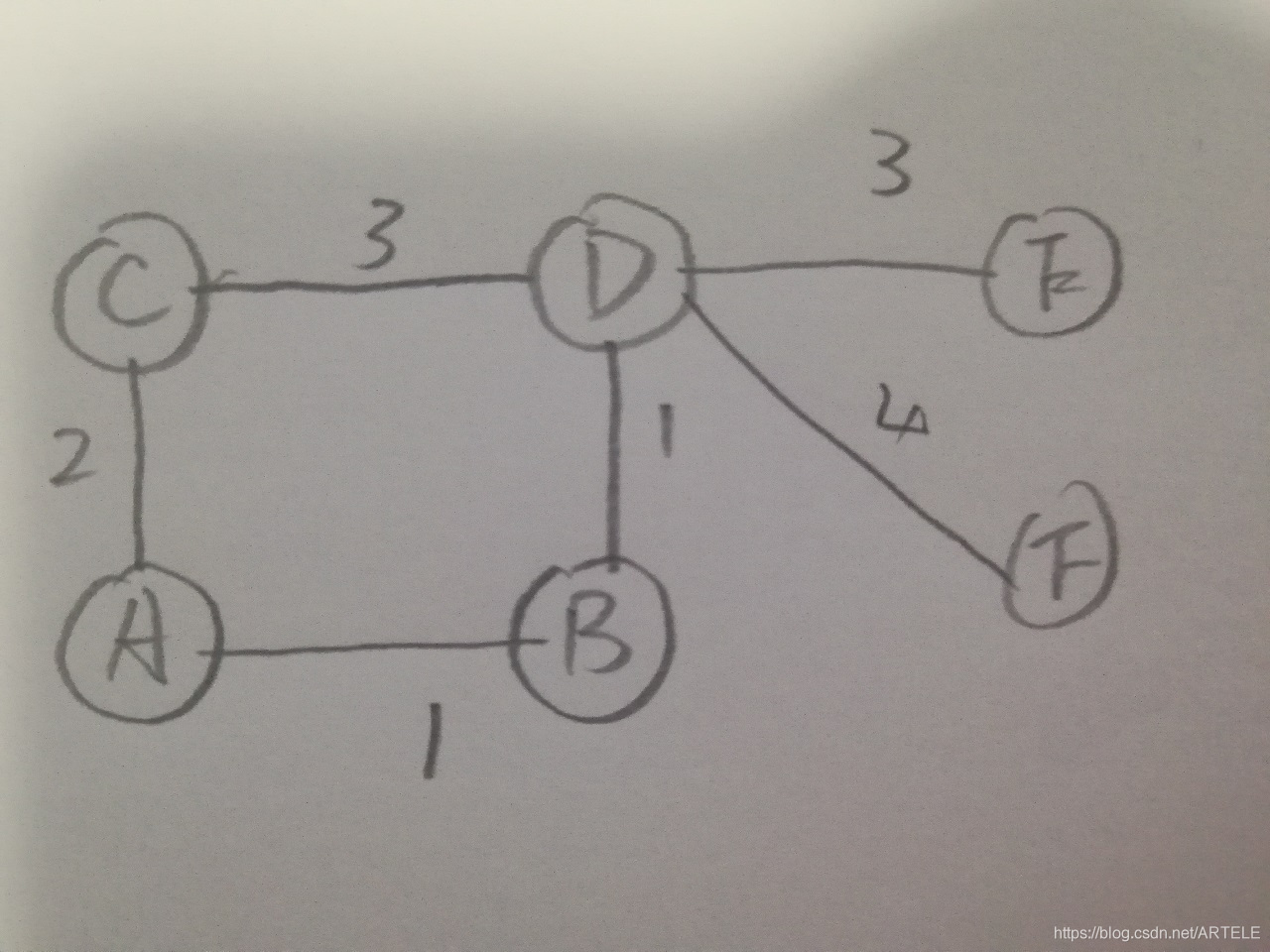
图1是例举的一个图。

在往下继续前，思考一个问题，假如从A点开始，那么找到与A连接的最短的边e，这条边另外一头与某点X相连，那么e是不是X到A的最短路径，答案:是。因为我们无法找到不走e并且还比e更短的路径了(没有负权值)，因为此时e就是让X到A最短的路径。在知道了这个前提之后，我们将这个理论简单命名为理论S，方便后面叙述，继续往下看。

图2 例子图2

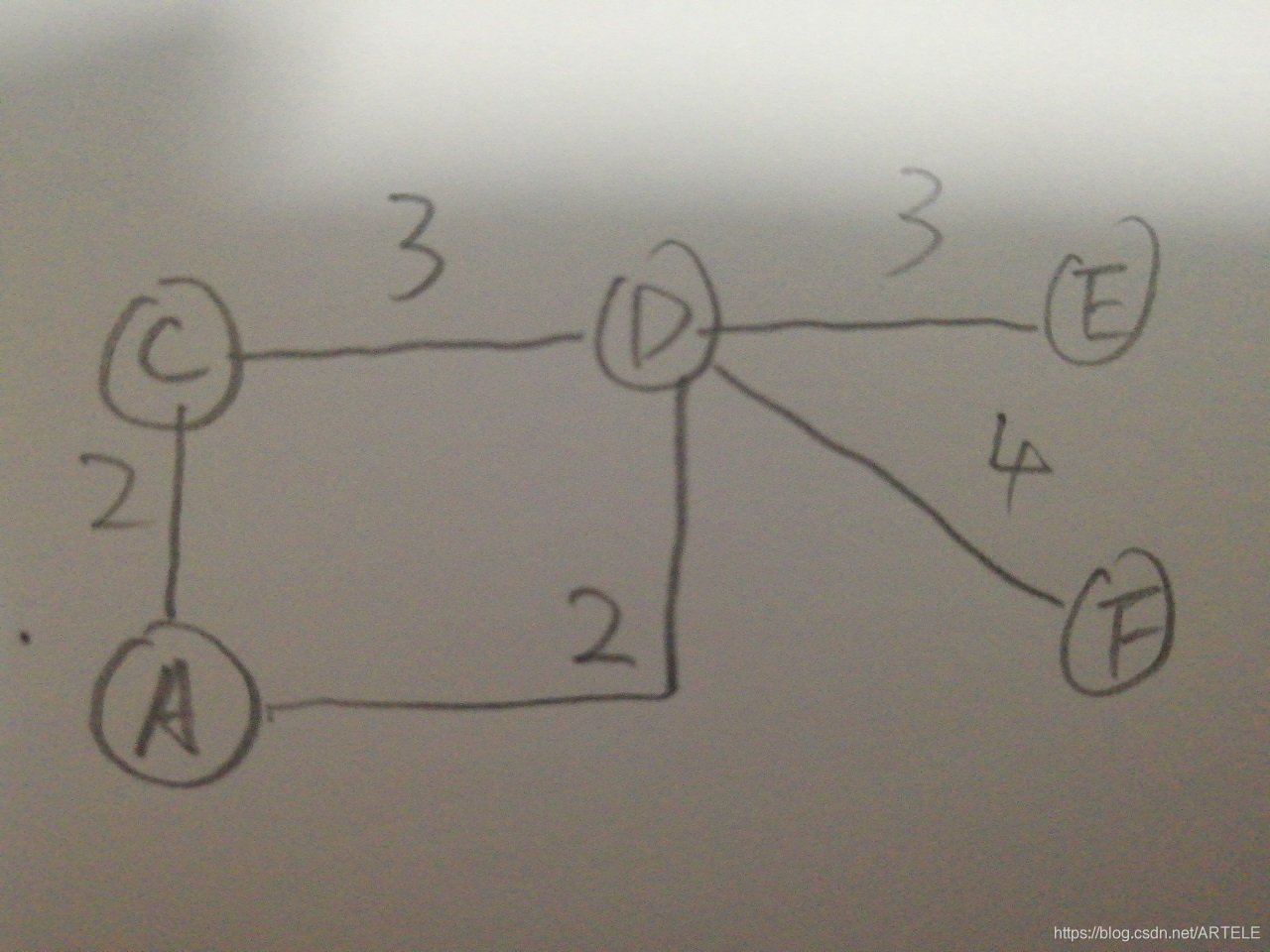
图2中少