【强化学习】强化学习数学基础：贝尔曼最优公式

强化学习的目的是寻找最优策略。这里学习贝尔曼最优公式需要重点关注两个概念和一个工具：

• 两个概念：optimal state value和optimal policy
• 一个基本工具：the Bellman optimality equation (BOE)

一个示例

还是从一个网格示例开始，如下所示：

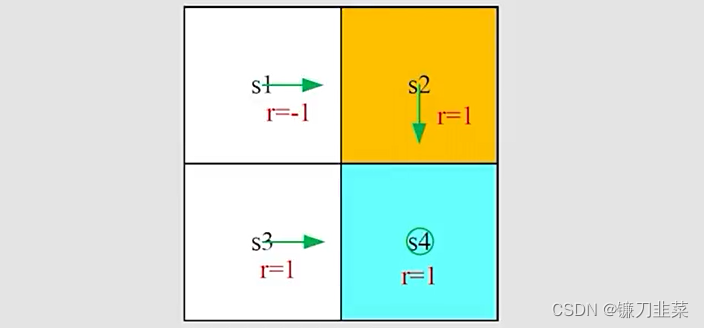
列出贝尔曼公式：

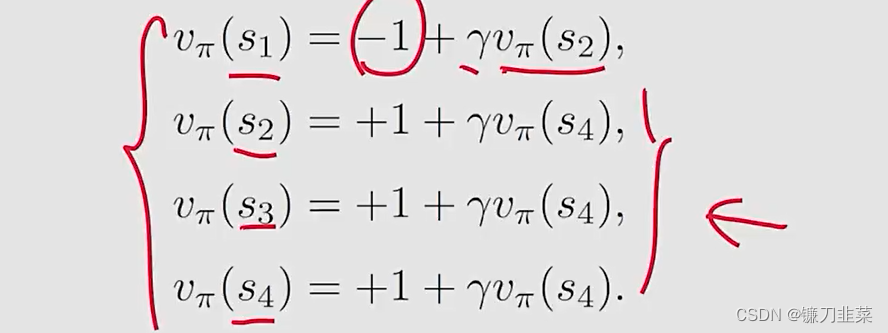
求解State value：令$\gamma =0.9$，然后，计算结果如下：
$$v_{\pi }(s_4)=v_{\pi }(s_3)=v_{\pi }(s_2)=10,v_{\pi }(s_1)=8$$
有了state value，求解Action value，考虑$s_1$，有：
$$q_{\pi }(s_1,a_1)=-1+\gamma v_{\pi }(s_1)=6.2$$
$$q_{\pi }(s_1,a_2)=-1+\gamma v_{\pi }(s_2)=8$$
$$q_{\pi }(s_1,a_3)=0+\gamma v_{\pi }(s_3)=9$$
$$q_{\pi }(s_1,a_4)=-1+\gamma v_{\pi }(s_1)=6.2$$
$$q_{\pi }(s_1,a_5)=0+\gamma v_{\pi }(s_1)=7.2$$

那么问题来了，当前策略不太好，如何改善这个策略？这个就依赖Action values。当前的策略$\pi (a|s_1)$可以写为：
$$\pi (a|s_1)=\{\begin{array}{ll}1& a=a_2\\ 0& a\ne a_2\end{array}$$
根据上面action value，可以发现$q_{\pi }(s_1,a_3)=9$是最大值，所以如果选择a3作为新策略，那么一个新策略描述为：
$$\pi (a|s_1)=\{\begin{array}{ll}1& a=a^{\ast }\\ 0& a\ne a^{\ast }\end{array}$$
其中$a^{\ast }=argma{x}_a{q}_{}$