值迭代与策略迭代
1. 值迭代算法(Value iteration algorithm)
如下,如何求解Bellman Optimality Equation? v = f ( v ) = max π ( r π + γ P π v ) v=f(v)=\max_{\pi}(r_\pi +\gamma P_\pi v) v=f(v)=πmax(rπ+γPπv)
根据之前的内容,我们知道可以采用contraction mapping theorem使用迭代算法求解: v k + 1 = f ( v k ) = max π ( r π + γ P π v k ) , k = 1 , 2 , 3 , . . . v_{k+1}=f(v_k)=\max_{\pi} (r_\pi +\gamma P_\pi v_k), k=1,2,3,... vk+1=f(vk)=πmax(rπ+γPπvk),k=1,2,3,...,其中 v 0 v_0 v0是一个任意值。
- 该算法最终能够发现最优状态值(optimal state value)和一个最优策略(optimal policy)
- 该算法被称为
value iteration
值迭代算法详细过程: v k + 1 = f ( v k ) = max π ( r π + γ P π v k ) , k = 1 , 2 , 3... v_{k+1}=f(v_k)=\max_\pi (r_\pi +\gamma P_\pi v_k), k=1,2,3... vk+1=f(vk)=πmax(rπ+γPπvk),k=1,2,3...可以分解为两部:
- Step 1:
policy update, 这一步是求解 π k + 1 = a r g max π ( r π + γ P π v k ) \pi_{k+1}=arg\max_\pi (r_\pi +\gamma P_\pi v_k) πk+1=argπmax(rπ+γPπvk)其中 v k v_k vk是给定的 - Step 2:
value update, v k + 1 = r π k + 1 + γ P π k + 1 v k v_{k+1}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_k vk+1=rπk+1+γPπk+1vk
问题: v k v_k vk是不是一个state value?当然不是,因为不能确定 v k v_k vk满足一个贝尔曼等式(Bellman equation)。
接下来,我们要研究elementwise form,目的是实现算法。
- Matrix-vector form适合于理论分析
- Elementwise form适合算法实现
Step1: Policy update
elementwise form如下: π k + 1 = a r g max π ( r π + γ P π v k ) \pi_{k+1}=arg\max_\pi (r_\pi +\gamma P_\pi v_k) πk+1=argπmax(rπ+γPπvk)即
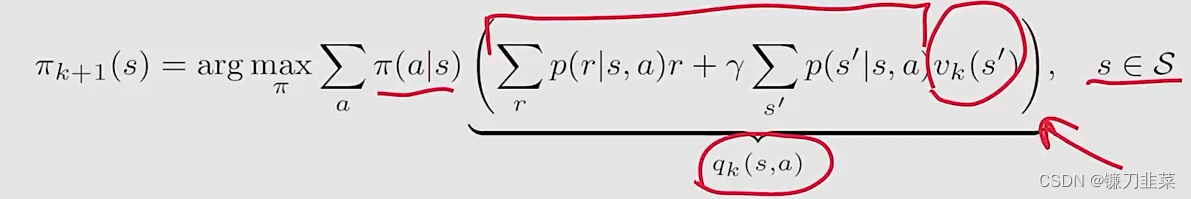
上面最优化问题的最优解是 π k + 1 ( a ∣ s ) = { 1 a = a k ∗ ( s ) 0 a ≠ a k ∗ ( s ) \pi_{k+1}(a|s)=\begin{cases}1 & a = a_k^*(s)\\0 & a\ne a_k^*(s)\end{cases} πk+1(a∣s)={
10a=ak∗(s)a=ak∗(s)其中 a k ∗ = a r g max a q k ( a , s ) a_k^*=arg\max_a q_k(a, s) ak∗=argmaxaqk(a,s)。 π k + 1 \pi_{k+1} πk+1被称为greedy policy,因为简单地选择最大的q-value。
Step2: Value update
elementwise form: v k + 1 = r π k + 1 + γ P π k + 1 v k v_{k+1}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_k vk+1=rπk+1+γPπk+1vk即
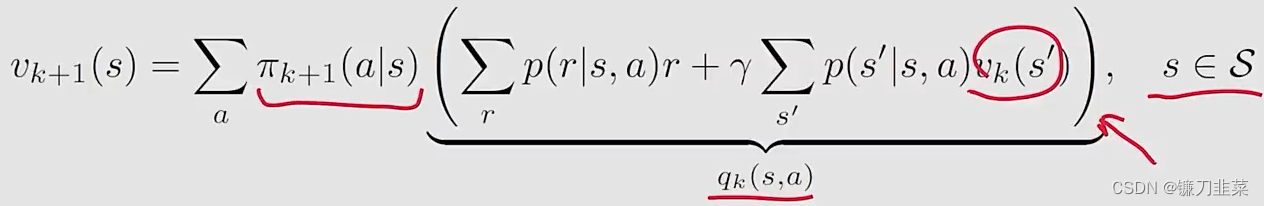
因为 π k + 1 \pi_{k+1} πk+1是greedy,上面等式可以简化为 v k + 1 ( s ) = max a q k ( a , s ) v_{k+1}(s)=\max_{a} q_k(a, s) vk+1(s)=amaxqk(a,s)
过程总结:
v k ( s ) → q k ( s , a ) → greedy policy π k + 1 ( a ∣ s ) → new value v k + 1 = max a q k ( s , a ) v_k(s)\rightarrow q_k(s, a)\rightarrow \text{ greedy policy }\pi_{k+1}(a|s)\rightarrow \text{ new value } v_{k+1}=\max_a q_k(s, a) vk(s)→qk(s,a)→ greedy policy πk+1





 值迭代和策略迭代是强化学习中两种重要的算法,用于解决贝尔曼最优公式。值迭代从一个初始值出发,通过不断迭代逼近最优状态值和策略。策略迭代则从初始策略开始,通过策略评估和策略改善逐步优化策略,直至找到最优策略。截断策略迭代是策略迭代的一种变体,限制了策略评估步骤的迭代次数。这些算法在实际应用中需要平衡计算效率和收敛速度。
值迭代和策略迭代是强化学习中两种重要的算法,用于解决贝尔曼最优公式。值迭代从一个初始值出发,通过不断迭代逼近最优状态值和策略。策略迭代则从初始策略开始,通过策略评估和策略改善逐步优化策略,直至找到最优策略。截断策略迭代是策略迭代的一种变体,限制了策略评估步骤的迭代次数。这些算法在实际应用中需要平衡计算效率和收敛速度。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 1366
1366

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










