强化学习学习笔记（3）---贝尔曼最优公式

本章主要内容

关键概念：最优状态值（optimal state value）和最优策略（ optimal policy）；
函数工具：贝尔曼最优方程（the Bellman optimality equation (BOE)）

一、激励性例子（Motivating examples）

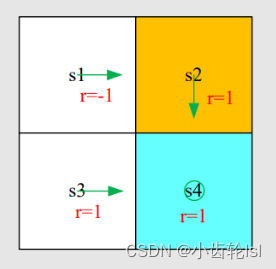
第一步：根据实例写出每个状态对应的贝尔曼方程：

第二步：求每个状态对应的状态值（state value），假定这里的=0.9，先由第四个式子求s4的状态值（state value），再求s1,s2,s3的状态值（state value）：

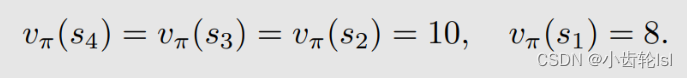
第三步：根据上一步求出的状态值（state value），再求出动作值（action value），这里以s1状态为例，求s1状态时各个动作的动作值（action value），每一个状态都有5个可采取的动作，故有相应的5个动作值（action value）,而每一个动作action也对应着一个策略和状态值（state value）：

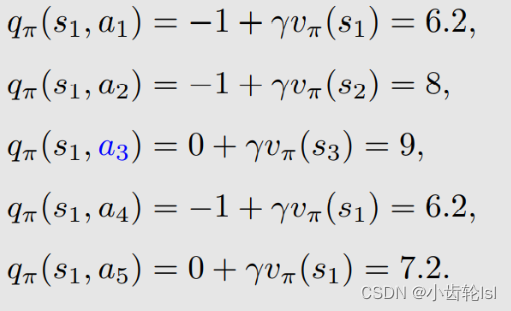
总结：从上述求解得到的动作值（action value）可知，在采取动作a3的时候值是最大的，因此这个策略也是最优的。采取动作a3的时候值是最大的原因是s3状态是一个可进入的网格。

改进：在上述例子中，可以看到在s1状态的时候，当前的策略是：

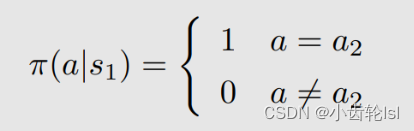
通过在第二步和第三步对状态值（state value）和动作值（action value）求解并对比之后可知，在s1状态时，采取动作a3的策略是最优的，因此我们选择一个新的策略（式子中的就是得到最优策略的动作，在本例中是a3）：

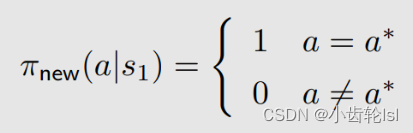
总结：

1. 动作值（action value）就是评估动作的主要参数，如果选择一个动作action之后，它对应的动作值action value很大，那么证明可以得到更多的reward，相应的策略也更好；
2. 在计算过程中，利用不断地迭代，就可以得到一个最优策略。就是首先对每个状态都选择 action value 最大的 action，选择完了一次，然后再来一次迭代得到一个新的策略，再迭代得到一个新的策略，最后那个策略一定会趋向一个最优的策略。

二、最优策略（Optimal policy）

状态值（state value） 是评估一个策略是否最优，如果有一个策略，它的状态值比在这个状态所有其他策略的状态值都要大，那么这个策略就是最优策略：

三、贝尔曼最优方程（Bellman optimality equation (BOE)）

贝尔曼最优方程：
方程中p(r|s, a), p(s'|s, a) 已知；v(s), v(s‘)未知要计算得到；π(s) 未知（贝尔曼公式依赖于一个给定的 π，而贝尔曼最优公式的 π 没有给定，需要求解）。 

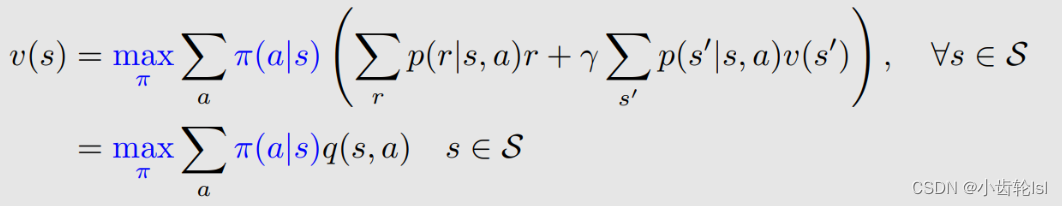
贝尔曼最优方程的矩阵向量形式Bellman optimality equation (matrix-vector form)：