用Keras快速实现Factorization Machines算法
用Keras快速实现Factorization Machines算法
在工业级程度的机器学习实践中,特征维往往非常巨大,包括稠密特征以及one-hot形式的大规模稀疏特征。随着特征维增加,基于传统的广义线模方法的统计假设:特征之间应保持独立不同分布,在大规模高维特征表征下几乎难以保证,同时高维稀疏特征如何有效表征,特征之间怎样有效组合,相对于LR(logistic regression),FM算法做了相应的改进。
Factorization Machines算法介绍
Factorization Machines(因子分解机, FM),这是一种新的模型,它结合了支持向量机(SVM)和因式分解模型的优点。FM是一种通用预测器(与SVM一样),能够处理任何实值数。另外,其使用分解参数模拟变量之间的所有交互(原文:In contrast to SVMs, FMs model all interactions between variables using factorized parameters.)。因此,即使在SVM也无力回天的稀疏性(如推荐系统)问题中,FM模型也能胜任。本文证明了FM的模型方程可以在线性时间内完成计算。
另一方面,有许多不同的因子分解模型,如矩阵分解;并行因子分析或专用模型,如SVD ++,PITF或FPMC。这些模型的缺点是它们不具有普遍适用性,仅适用于特殊输入数据。此外,他们的模型方程和优化算法也是针对特定任务的。FM仅通过指定输入数据(即特征向量)就可以模拟这些模型。这使得即使对于没有分解模型专业知识的用户,FM也很容易使用。
Factorization Machines算法原理
最早的广告点击率预估应用算法LR本质上其实是一个线性回归,数学表达为:
l
i
n
e
a
r
m
o
d
e
l
:
y
=
w
0
+
∑
i
=
1
n
w
i
x
i
linear\quad model: y=w_0+\sum _{i=1}^nw_ix_i
linearmodel:y=w0+i=1∑nwixi
在线性回归中,算法的统计假设前提是各个特征是独立的,不考虑特征间的相关联性。但是在实际的工程实践中,我们很难保证特征间的独立性。
为了让模型能够表征相互关联特征的融合表达,通常的做法是用多项式来表示,这里考虑二阶交互,即
x
i
x_i
xi和
x
j
x_j
xj的相互表达用
x
i
x
j
x_ix_j
xixj来表示,因此对于有限的
n
n
n维特征,特征的两两组合一共有
(
n
(
n
−
1
)
)
2
\frac{(n(n-1))}{2}
2(n(n−1))个新特征,FM的模型参数总计为
(
n
(
n
−
1
)
)
2
+
1
\frac{(n(n-1))}{2}+1
2(n(n−1))+1,可训练参数为
n
(
k
+
1
)
+
1
n(k+1)+1
n(k+1)+1,数学表达式为:
F
M
m
o
d
e
l
:
y
~
(
x
)
=
w
0
+
∑
i
=
1
n
w
i
x
i
+
∑
i
=
1
n
∑
j
=
i
+
1
n
w
i
j
x
i
x
j
FM\quad model: \widetilde{y}(x)=w_0+\sum_{i=1}^nw_ix_i+\sum _{i=1}^n\sum _{j=i+1}^n w_{ij}x_ix_j
FMmodel:y
(x)=w0+i=1∑nwixi+i=1∑nj=i+1∑nwijxixj
其中,
n
n
n代表样本的特征数量,
x
i
x_i
xi是第
i
i
i个特征的值,
w
0
,
w
i
,
w
i
j
w_0,w_i,w_{ij}
w0,wi,wij是模型参数,
w
i
j
∈
W
w_{ij} \in W
wij∈W表示第
i
i
i个变量和第
j
j
j个变量的交互作用(interaction),只有当
x
i
x_i
xi与
x
j
x_j
xj都不为0时,交叉才有意义。
由于线代中有如下定义:
如果一个实对称矩阵A正定,则A与E合同,那么存在可逆矩阵C,使得 A = C T C A=C^TC A=CTC
如果矩阵
W
W
W是正定矩阵,那么只要
k
k
k足够大,就存在
V
V
V使得
W
=
V
V
T
W=VV^T
W=VVT,其中
V
V
V是
n
×
k
n\times k
n×k的二维矩阵。因此可以将上面的式子转化为:
y
~
(
x
)
=
w
0
+
∑
i
=
1
n
w
i
x
i
+
∑
i
=
1
n
∑
j
=
i
+
1
n
<
v
i
,
v
j
>
x
i
x
j
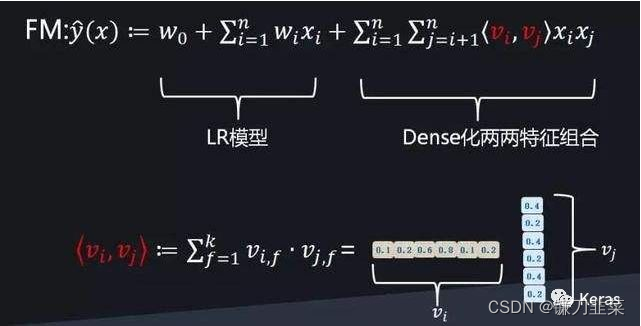
\widetilde{y}(x)=w_0+\sum_{i=1}^n{w_ix_i}+\sum_{i=1}^n\sum_{j=i+1}^n {\lt \bold{v}_i,\bold{v}_j \gt x_ix_j}
y
(x)=w0+i=1∑nwixi+i=1∑nj=i+1∑n<vi,vj>xixj
其中
<
⋅
,
⋅
>
\lt ·,·\gt
<⋅,⋅>表示维数为
k
k
k的向量的点乘,
k
k
k为超参数,决定因子分解的维度:
<
v
i
,
v
j
>
:
=
∑
f
=
1
k
v
i
,
f
⋅
v
j
,
f
\lt \bold{v}_i,\bold{v}_j \gt :=\sum_{f=1}^k{v_{i,f}·v_{j,f}}
<vi,vj>:=f=1∑kvi,f⋅vj,f
v
i
∈
V
\bold{v}_i \in \bold{V}
vi∈V表示第
i
i
i个变量的
k
k
k个因子组成的向量。
不过在数据稀疏的情况下,应该选择较小的 k k k,因为可能没有足够的数据来估计矩阵 W W W。限制 k k k的大小能够使得FM模型更加通用,能够提高其泛化能力。
当
n
n
n趋于无穷时,模型参数以幂级增长,特征维度增加不可避免会带来特征的大规模稀疏性,算法计算相当耗时,计算时间复杂度为
O
(
k
n
2
)
O(kn^2)
O(kn2)。
FM算法改进
直接对两两组合的特征进行参数拟合计算时间复杂度难以接受,为了降低模型的时间复杂度,我们可以对
w
i
j
w_{ij}
wij做一个矩阵变换,简单的说,对每一个特征,我们都初始化一个隐含向量(lantent vector)
A
i
=
[
v
i
1
,
v
i
2
,
…
,
v
i
k
]
T
A_i = [v_{i1}, v_{i2},…,v_{ik}]^T
Ai=[vi1,vi2,…,vik]T,
k
k
k是一个模型参数,一般设置为 30 或 40,因此模型数学表达为:
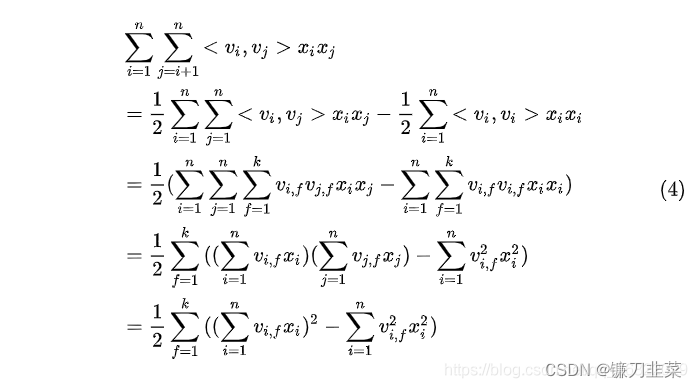
因此,有:
F
M
m
o
d
e
l
:
y
=
w
0
+
∑
i
=
1
n
w
i
x
i
+
1
2
∑
f
=
1
k
(
(
∑
i
=
1
n
v
i
,
f
x
i
)
2
−
∑
i
=
1
n
v
i
,
f
2
x
i
2
FM\quad model: y=w_0+\sum_{i=1}^nw_ix_i+\frac{1}{2}\sum_{f=1}^k((\sum_{i=1}^nv_{i,f}x_i)^2-\sum _{i=1}^nv_{i,f}^2x_i^2
FMmodel:y=w0+i=1∑nwixi+21f=1∑k((i=1∑nvi,fxi)2−i=1∑nvi,f2xi2
从上面的描述可以知道FM可以在线性的时间内进行预测。因此模型的参数(
w
0
,
w
和
V
w_0, \bold{w}和\bold{V}
w0,w和V)可以通过梯度下降的方法(例如随机梯度下降)来学习。FM模型的梯度是:
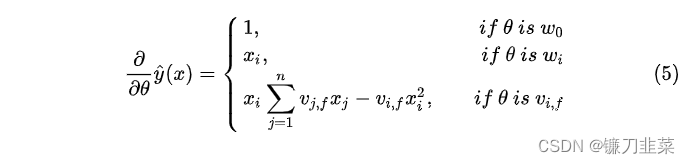
由于
∑
j
=
1
n
v
j
,
f
x
j
\sum_{j=1}^n{v_{j,f}x_j}
∑j=1nvj,fxj与
i
i
i是独立的,因此可以提前计算其结果。并且每次梯度更新可以在常数时间复杂度内完成,因此FM参数训练的复杂度也是
O
(
k
n
)
O(kn)
O(kn)。综上可知,FM可以在线性时间训练和预测,是一种非常高效的模型。
FM算法扩展到d-阶
前面都是针对2阶FM模型进行讨论,这个模型可以直接拓展到d阶:
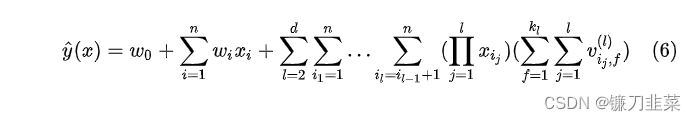
其中第
l
l
l个交互作用项的参数可以通过PARAFAC模型的参数:
V
l
∈
R
n
×
k
l
,
k
l
∈
N
0
+
V^{l}\in \mathbb{R}^{n\times k_l}, k_l \in \mathbb{N}_0^+
Vl∈Rn×kl,kl∈N0+
如果直接计算上面公式的时间复杂度为 O ( k d n d ) O(k_dn^d) O(kdnd),如果进行优化,其时间复杂度也会是线性的。
FM适用预测任务
FM 适用预测任务:
- ``Regression`:FM 本质上是广义线模,能够通过最小化MSE损失来实现回归预测;
Binary classification:FM 模型输出结果施加一个 sigmoid 函数,通过最小化 binary crossentropy损失来实现二分类预测;Ranking:通过对向量 X X X预测的分数 Y Y Y,可以对成对向量( X 1 X_1 X1, X 2 X_2 X2)进行排序。
FM 算法优点:
- 对稀疏数据能够进行有效的参数估计;
- FM 模型的具有线性的时间复杂度,计算速度快;
- FM 模型能够拟合任意实数特征的二次项参数分布;
SVM和FM模型对比
- 为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢?
- 线性SVM只有一维特征,不能挖掘深层次的组合特征在实际预测中并没有很好的表现;
- 而多项式SVM正如前面提到的,交叉的多个特征需要在训练集上共现才能被学习到,否则该对应的参数就为0,这样对于测试集上的case而言这样的特征就失去了意义,因此在稀疏条件下,SVM表现并不能让人满意。
- 而FM不一样,通过向量化的交叉,可以学习到不同特征之间的交互,进行提取到更深层次的抽象意义。
- 此外,FM和SVM的区别还体现在:
- FM可以在原始形式下进行优化学习,而基于kernel的非线性SVM通常需要在对偶形式下进行;
- FM的模型预测是与训练样本独立,而SVM则与部分训练样本有关,即支持向量。
SVM和FM模型区别总结
- SVM的密集参数化需要直接观察相互作用,而这通常是在稀疏环境中无法获得的。 然而即使在稀疏情况下,FM的参数也可以很好地进行参数估计。
- FM可以直接在原始的模型公式上进行学习,而SVM需要模型推导
- FM模型不依赖于训练集,而SVM依赖于训练集(支持向量和训练集中的数据有关)
用Keras实现FM模型
数据采用威斯康辛州的乳腺癌分类数据集,一共有30个特征。LR的权重参数施加了L1正则化,在高维特征下容易产生稀疏解,偏置项施加的是L2正则,交叉项部分自定义层实现,采用改进后的优化方法。整个模型损失函数采用二分类的交叉熵损失,即对数损失(logloss),梯度优化器使用adam方法,度量函数则是使用accurary。
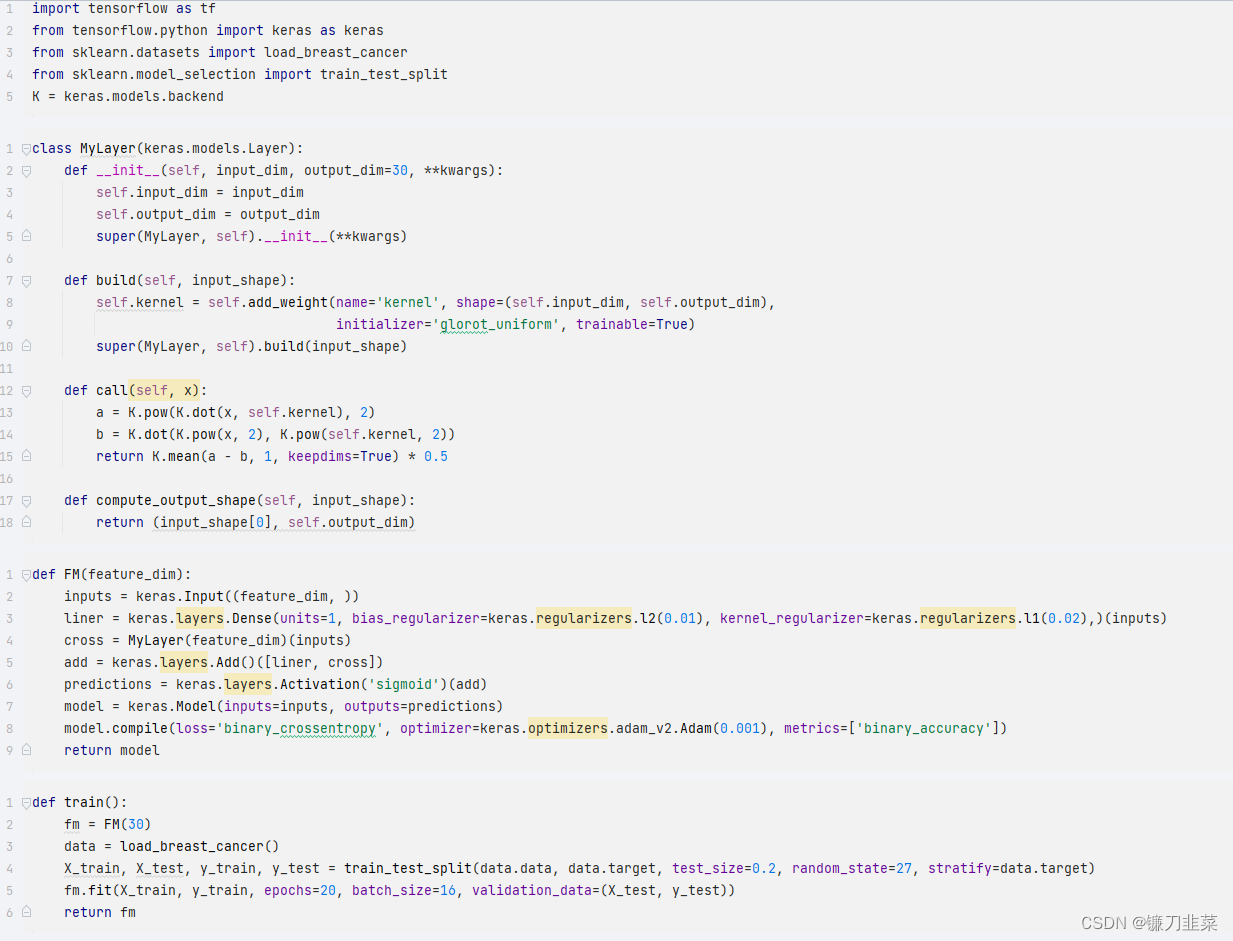
在完成了模型的构建后, 可以使用 fm.summary() 来观察一下模型的层和参数情况:
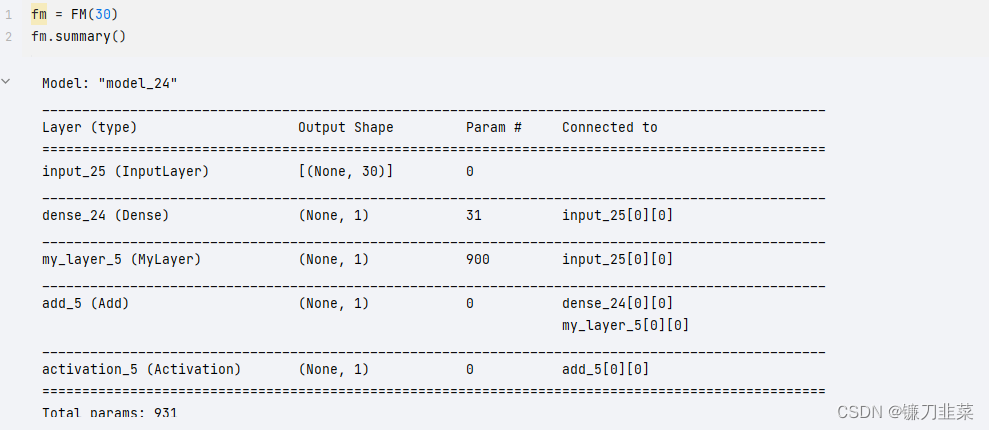
可以看出,模型的参数由3030的矩阵加上逻辑回归的参数一共有3030+30+1=931个。
执行模型的训练:
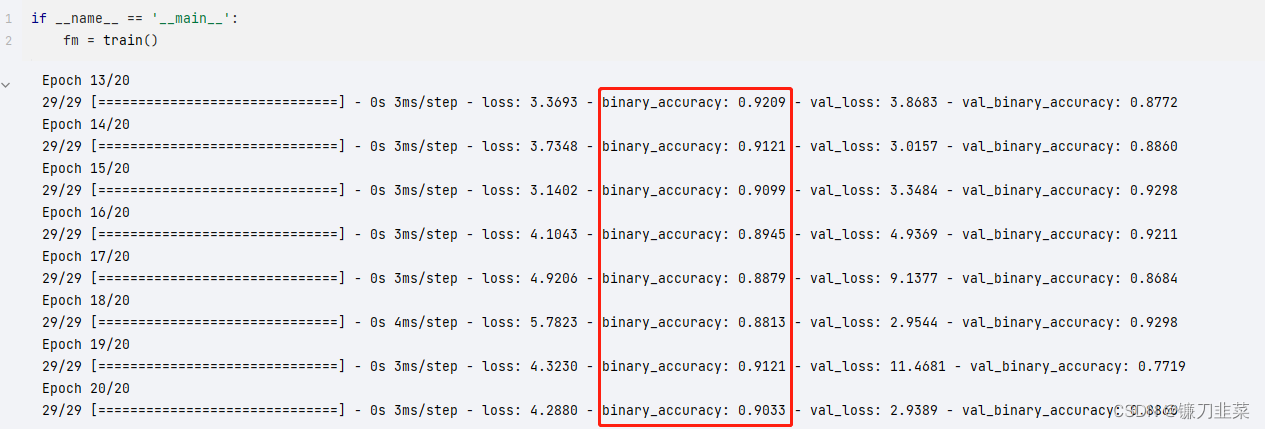
参考资料
[1] Factorization Machines
[2] [论文阅读]Factorization Machines
[3] FM系列算法解读(FM+FFM+DeepFM)








 本文介绍了Factorization Machines(FM)算法及其原理,并对比了FM与SVM的不同之处。FM算法能够处理稀疏数据并有效估计参数,适用于回归、二分类及排序等任务。文中详细解释了FM模型的数学表达式及其优化过程,并给出了使用Keras实现FM模型的具体步骤。
本文介绍了Factorization Machines(FM)算法及其原理,并对比了FM与SVM的不同之处。FM算法能够处理稀疏数据并有效估计参数,适用于回归、二分类及排序等任务。文中详细解释了FM模型的数学表达式及其优化过程,并给出了使用Keras实现FM模型的具体步骤。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










