【Keras】用Keras实现Field-aware Factorization Machine算法

用Keras实现Field-aware Factorization Machine(FFM)算法

在CTR预估中，通常会遇到one-hot类型的变量，会导致数据特征的稀疏。为解决这个问题，FFM在FM的基础上进一步改进，在模型中引入类别的概念，即field。将同一个field的特征单独进行one-hot，因此在FFM中，每一维特征都会针对其他特征的每个field，分别学习一个隐变量，该隐变量不仅与特征相关，也与field相关。

FFM的算法原理

假设样本的$n$个特征属于$f$个field，那么FFM的二次项有$nf$个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看做FFM的特例，把所有特征都归属到一个field的FFM模型。
换句话说，在FFM算法中，每一维特征$x_i$对任意$x_j(i\ne j)$，都会在其对应的field $f_j$，去学习一个隐向量$V_{i,f_j}$，所以每个特征都会有一个field-lantent矩阵，shape=[f, k]，f为field的维度，k为隐向量的维度。其模型方程为：
$$y(X)=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n\sum _{j=i+1}^n<V_{i,f_j},V_{j,f_i}>x_i{x}_j$$
如果隐向量的长度为$k$，那么FFM的二次参数有$nfk$个，远多于FM模型的$nk$个。

FFM的参数：

• FFM 模型的参数与 FM 一样，模型参数总计为$\frac{n(n+1)}{2}+1$；
• 引入隐向量和特征域属性，实际可训练参数为$n(f\ast k+1)+1$；

FFM的损失函数：
FFM将问题定义为分类问题，使用的是logistic loss，同时加入正则项：
$$mi{n}_w\sum _{i=1}^{L}log(1+exp(-y_i\varphi (w,x_i)))+\frac{\lambda }{2}||w|{|}^2$$

FFM的优化方法：随机梯度下降
梯度下降方法有很多种，根据为提高效率分别衍生了批量梯度下降，随机梯度下降及小批量梯度下降，根据需求选择即可。

FFM的训练过程：

注：Paper使用AdaGrad进行优化训练。

从 FFM 模型的表达式可以看出，如果把field设为 1，那么 FFM 模型就是 FM 模型，因此 FM 模型只是 FFM 模型中特征在一个域中的表征。 由于 FFM 模型的二次项每次只训练特定域的隐含向量，所以数学上不能进一步化简，从而造成计算相当耗时，模型计算复杂度为$O(k{n}^2)$，远高于FM算法，实际工程上很少使用。

FFM模型训练注意细节：

• 样本归一化。FFM默认是进行样本数据的归一化。如果不做归一化，很容易造成数据inf溢出，进而引起梯度计算的nan错误；
• 特征归一化。数值型和类别型特征生成尺度大小不一，将源数值型特征的值归一化到 [0,1] 是非常必要的。
• 省略零值特征。从FFM模型的表达式可以看出，零值特征对模型完全没有贡献。因为零值特征的一次项和组合项均为零，梯度下降对该特征权重的更新没有任何有益的表现，并且还可以提高模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

FFM的应用

在DSP或者推荐场景中，FFM主要用来评估站内的CTR和CVR，即一个用户对一个商品的潜在点击率和点击后的转化率。CTR和CVR预估模型都是在线下训练，然后线上预测。两个模型采用的特征大同小异，主要分三类：

• 用户相关的特征: 年龄、性别、职业、兴趣、品类偏好、浏览/购买品类等基本信息，以及用户近期点击量/购买量/消费额等统计信息
• 商品相关的特征: 商品所属品类、销量、价格、评分、历史CTR/CVR等信息
• 用户-商品匹配特征: 浏览/购买品类匹配、浏览/购买商家匹配、兴趣偏好匹配等

FFM 适用预测任务： 同FM算法一样，具备FM算法的应用的相同任务。

• Regression：FFM 本质上是广义线模，能够通过最小化MSE 损失来实现回归预测；
• Binary classification：FFM 模型输出结果施加一个 sigmoid 函数，通过最小化 binary crossentropy损失来实现二分类预测；
• Ranking：通过对向量 X预测的分数 Y，可以对成对向量($X_1,X_2$)进行排序。

FFM 算法优缺点：

• 对稀疏数据能够进行有效的参数估计；
• FFM 模型时间复杂度是非线性的，计算速度非常慢；
• FFM 模型能够拟合任意实数特征的二次项参数分布；
• FFM对不同域的特征组合具有比FM更好的表达；

FFM应用举例

下面以一个例子简单说明FFM的特征组合方式。输入记录如下：

这条记录可以编码成5个特征，其中“Genre=Comedy”和“Genre=Drama”属于同一个field，“Price”是数值型，不用One-Hot编码转换。为了方便说明FFM的样本格式，我们将所有的特征和对应的field映射成整数编号。

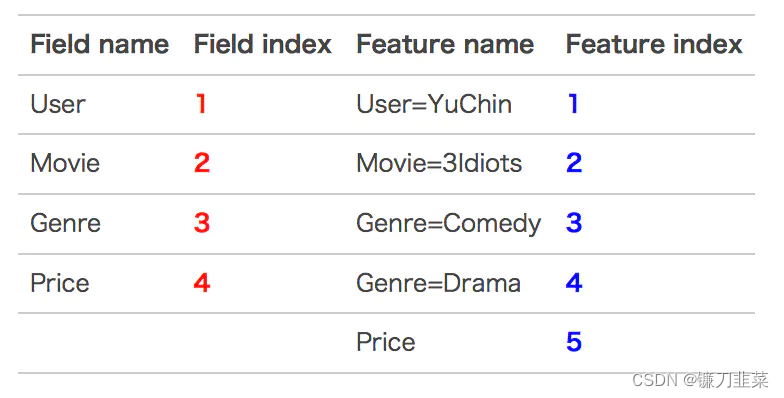
那么，FFM的组合特征有10项，如下图所示：

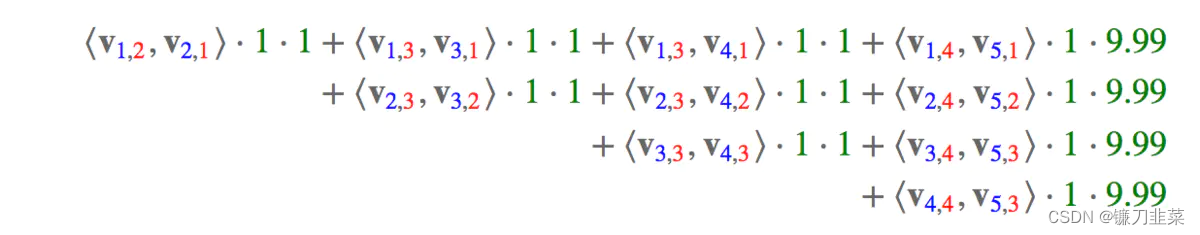
其中，红色是field编号，蓝色是特征编号。

FFM算法的Keras实现

import tensorflow as tf
from tensorflow.python import keras as keras
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

K = keras.models.backend
field_cross = tf.Variable(0., dtype='float32')

# 自定义交叉特征层
class MyLayer(keras.models.Layer):
    def __init__(self, field_dict, field_dim, input_dim, output_dim=30, **kwargs):
        self.field_dict = field_dict
        self.field_dim = field_dim
        self.input_dim = input_dim
        self.output_dim = output_dim
        super(MyLayer, self).__init__(**kwargs)

    def build(self, input_shape):
        self.kernel = self.add_weight(name='kernel',
                                      shape=(self.input_dim, self.field_dim, self.output_dim),
                                      initializer='glorot_uniform',
                                      trainable=True)
        super(MyLayer, self).build(input_shape)

    def call(self, x):
        self.field_cross = field_cross
        for i in range(self.input_dim):
            for j in range(i+1, self.input_dim):
                weight = tf.math.reduce_sum(tf.math.multiply(self.kernel[i, self.field_dict[j]], self.kernel[j, self.field_dict[i]]))
                value = tf.math.multiply(weight, tf.math.multiply(x[:,i], x[:,j]))
                self.field_cross = tf.math.add(self.field_cross, value)
        return self.field_cross

    def compute_output_shape(self, input_shape):
        return (input_shape[0], 1)

# 实现FFM算法
def FFM(feature_dim, field_dict, field_dim, output_dim=30):
    inputs = keras.Input((feature_dim,))
    liner = keras.layers.Dense(1)(inputs)
    cross = MyLayer(field_dict, field_dim, feature_dim, output_dim)(inputs)
    cross = keras.layers.Reshape((1,))(cross)
    add = keras.layers.Add()([liner, cross])
    predictions = keras.layers.Activation('sigmoid')(add)
    model = keras.Model(inputs=inputs, outputs=predictions)
    model.compile(loss='binary_crossentropy', optimizer=keras.optimizers.adam_v2.Adam(0.001),
                  metrics=['binary_accuracy'])
    return model


def train():
    field_dict = {i: i // 5 for i in range(50)}
    ffm = FFM(30, field_dict, 6, 50)
    data = load_breast_cancer()
    X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=27,
                                                        stratify=data.target)
    ffm.fit(X_train, y_train, epochs=10, batch_size=16, validation_data=(X_test, y_test))
    return ffm


if __name__ == '__main__':
    ffm = train()

在FFM算法中，feature_dim是特征的维数， field_dict是一个特征维与域维的两两整数映射的字典，field_dim是域的维数，output_dim则是隐向量的维度。

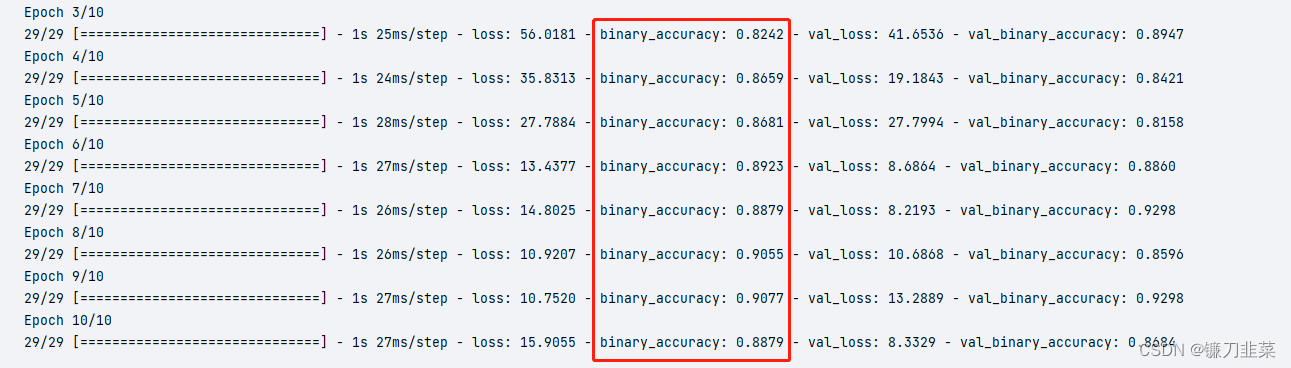
执行结果：

参考资料

[1] FM系列算法解读（FM+FFM+DeepFM）
[2] 推荐系统遇上深度学习(二)–FFM模型理论和实践
[3] https://www.csie.ntu.edu.tw/~r01922136/slides/ffm.pdf