用Keras快速实现Logistic Regression算法
用Keras快速实现Logistic Regression算法
Logistic Regression(LR),即逻辑回归,是最简单的广义线性模型。在CTR(Click-Through-Rate,即点击通过率,是互联网广告常用的术语)预估的算法中,是一个简单的,有代表性的算法。LR计算速度非常快,在人工特征工程的辅助下,一般可以得到较好的结果。
Logistic Regression算法原理
LR算法是建立在线性回归算法之上,套用了一个逻辑函数。对于线性边界的情况,边界形式可以归纳为如下公式:
θ
0
+
θ
1
x
1
+
,
.
.
.
,
+
θ
n
x
n
=
∑
i
=
1
n
θ
i
x
i
=
θ
T
x
\theta _0+\theta _1x_1+,...,+\theta _nx_n=\sum _{i=1}^n\theta _ix_i=\theta ^Tx
θ0+θ1x1+,...,+θnxn=i=1∑nθixi=θTx
也就是一个简单的
y
=
w
x
+
b
y=wx+b
y=wx+b的数学表达式,之后再套用一个逻辑函数:
h
θ
(
x
)
=
g
(
θ
T
x
)
1
1
+
e
−
θ
T
x
h_\theta (x)=g(\theta ^Tx)\frac{1}{1+e^{-\theta ^Tx}}
hθ(x)=g(θTx)1+e−θTx1
这个逻辑函数也就是sigmoid激活函数,它使得线性回归的实数阈值空间经过非线性函数变换映射到一个
0
∼
1
0\sim 1
0∼1的数值空间,也就成了一个预测概率大小的可能性。
sigmoid激活函数的曲线如下:
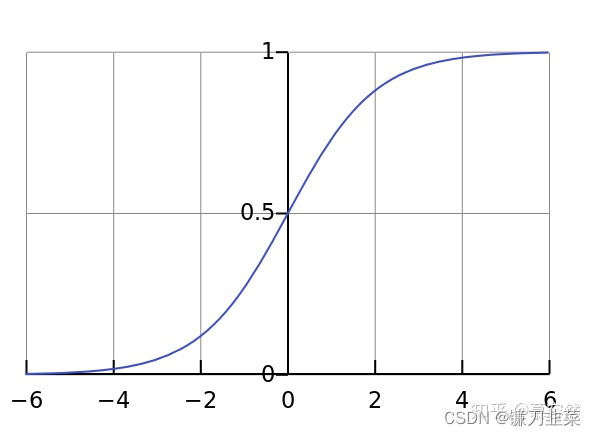
从图中我们可以看到sigmoid激活函数的自变量取值空间在[-4,4]的区间内对概率输出变化比较敏感,有效激活取值其实很小,从这一方面来看其实这也是sigmoid函数最大的缺点。
Logistic回归模型的适用条件
Logistic回归模型的适用条件:
- 因变量为二分类的分类变量或某事件的发生率,并且是数值型变量;
- 残差和因变量都要服从二项分布;
- 自变量和Logistic概率是线性关系;
- 各观测对象间相互独立;
Logistic回归模型的注意事项
(1)过拟合问题
过拟合问题往往源自过多的特征,冗余的特征往往对模型的预测有较大的干扰。解决的方法:
- 一是特征筛选,去除有效性较低的特征;
- 二是采用正则化,正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
J ( θ ) = 1 2 m ∑ i = 1 n ( h θ ( x i ) − y i ) 2 + λ ∑ j = 1 n θ j 2 J(\theta )=\frac{1}{2m}\sum _{i=1}^n(h_\theta (x_i)-y_i)^2+\lambda \sum _{j=1}^n \theta _j^2 J(θ)=2m1i=1∑n(hθ(xi)−yi)2+λj=1∑nθj2
(2)特征处理
LR建模特征处理为保证模型的稳定性,每个入模特征一般都需要进行分箱处理,这在信贷风控建模中尤为常见,类别变量类别数较少时则不需要分组,类别数较多或连续变量则要进行分组优化,常用的分组方法包括等频分箱、等宽分箱等。
Keras实现Logistic Regression算法
数据采用威斯康辛州的乳腺癌分类数据集,一共有30个特征。LR的权重参数施加了L1正则化,在高维特征下容易产生稀疏解,偏置项施加的是L2的正则。整个模型损失函数采用二分类的交叉熵损失,即对数损失(logloss),梯度优化器使用adam方法,度量函数则是使用accurary。

在完成了模型的构建后, 可以使用 lr.summary() 来观察一下模型的层和参数情况:
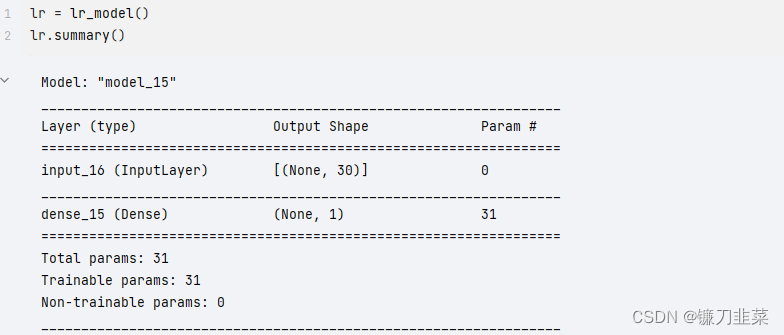
经过100个epoch的训练,训练集的loss下降有所波动,而验证集的acc达到90%左右,可以通过增加epoch,调整batch_size,以及正则化参数等措施来提高模型训练效果。
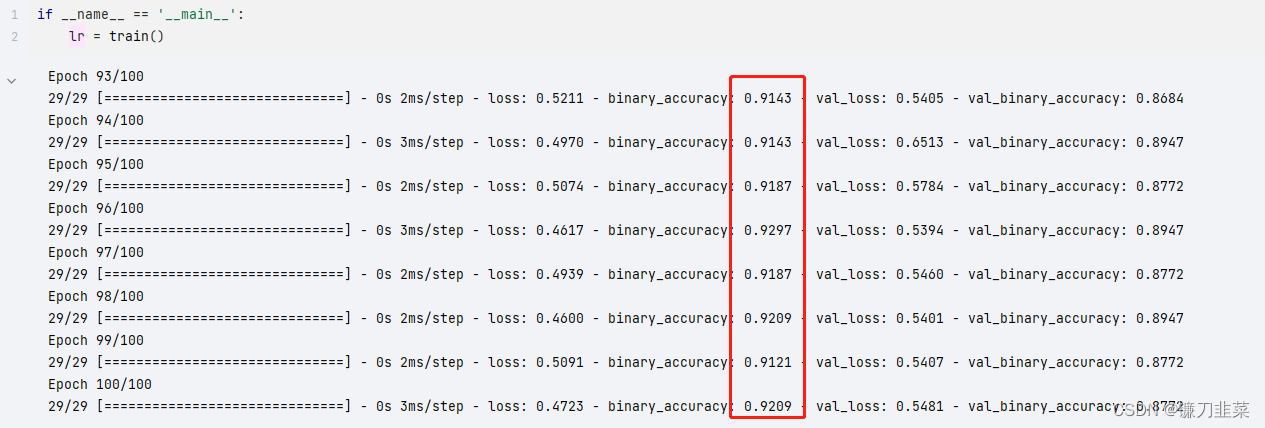
整个建模过程使用tensorflow的keras接口来编程,原因在于tf.keras是由纯tensorflow实现,与tf具有非常好的兼容性,特别是tf-2.0版本后将于tf.kears在诸多功能下完美集成,后续实现默认均由tf.keras代替keras来进行高效编程。










 本文介绍了如何使用Keras快速实现Logistic Regression算法。详细解释了Logistic Regression的基本原理及适用条件,并通过威斯康辛州乳腺癌数据集演示了算法的具体实现过程。
本文介绍了如何使用Keras快速实现Logistic Regression算法。详细解释了Logistic Regression的基本原理及适用条件,并通过威斯康辛州乳腺癌数据集演示了算法的具体实现过程。

















 6538
6538

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










