【每日一题】在二叉树中找到两个节点的最近公共祖先

在二叉树中找到两个节点的最近公共祖先

题目来源：牛客网 BM38 在二叉树中找到两个节点的最近公共祖先

描述

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足 $1\le n\le 10^5$, 节点值val满足区间 [0,n)
要求：时间复杂度 O(n)

注：本题保证二叉树中每个节点的val值均不相同。

如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

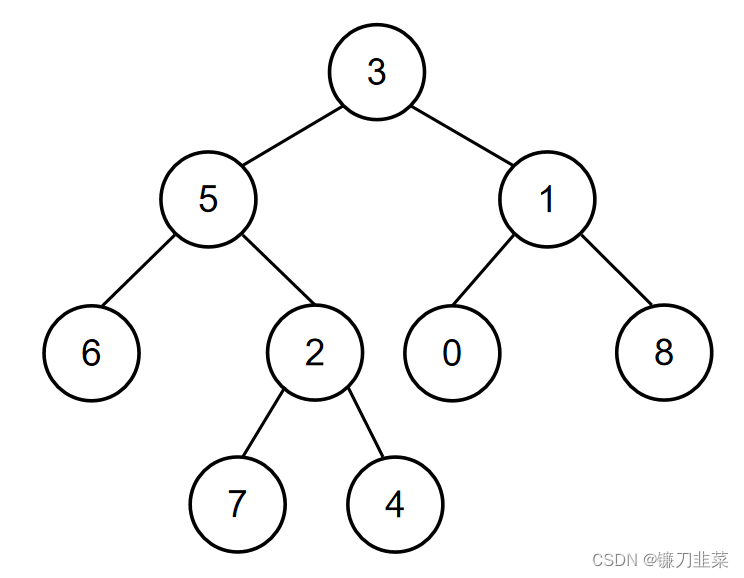
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。
节点本身可以视为自己的祖先
示例1

输入：
{3,5,1,6,2,0,8,#,#,7,4},5,1
返回值：
3

示例2

输入：
{3,5,1,6,2,0,8,#,#,7,4},2,7
返回值：
2

解题思路

---

深度优先搜索（dfs）
深度优先搜索一般用于树或者图的遍历，其他有分支的（如二维矩阵）也适用。它的原理是从初始点开始，一直沿着同一个分支遍历，直到该分支结束，然后回溯到上一级继续沿着一个分支走到底，如此往复，直到所有的节点都有被访问到。

---

思路
既然要找到二叉树中两个节点的最近公共祖先，那我们可以考虑先找到两个节点全部祖先，可以得到从根节点到目标节点的路径，然后依次比较路径得出谁是最近的祖先。
找到两个节点的所在可以深度优先搜索遍历二叉树所有节点进行查找。

具体做法

1. 利用dfs求得根节点到两个目标节点的路径：每次选择二叉树的一棵子树往下找，同时路径数组增加这个遍历的节点值。
2. 一旦遍历到了叶子节点也没有，则回溯到父节点，寻找其他路径，回溯时要去掉数组中刚刚加入的元素。
3. 然后遍历两条路径数组，依此比较元素值
4. 找到两条路径第一个不相同的节点即是最近公共祖先

代码

Java

import java.util.*;
public class Solution{
	// 记录是否找到到o的路径
	public boolean flag = false;
	// 求得根节点到目标节点的路径
	public void dfs(TreeNode root, ArrayList<Integer> path, int o){
		if (flag || root == null)
			return;
		path.add(root.val);
		// 节点值都不同，可以直接用值比较
		if (root.val == o){
			flag = true;
			return;
		}
		// dfs遍历查找
		dfs(root.left, path, o);
		dfs(root.right, path, o);
		// 找到
		if(flag){
			return;
		}
		// 回溯
		path.remove(path.size() - 1);
	}
	public int lowestCommonAncestor(TreeNode root, int o1, int o2){
		ArrayList<Integer> path1 = new ArrayList<Integer>();
		ArrayList<Integer> path2 = new ArrayList<Integer>();
		// 求根节点到两个节点的路径
		dfs(root, path1, o1);
		// 重置flag, 查找下一个
		flag = false;
		dfs(root, path2, o2);
		int res = 0;
		// 比较两个路径，找到第一个不同的点
		for(int i = 0; i< path1.size() && i<path2.size();i++){
			int x = path1.get(i);
			int y = path2.get(i)
			if (x == y){
				res = x;
			}else{
				break;
			}
		}
		return res;
	}
}

Python

# -*- coding: utf-8 -*-#

# ----------------------------------------------
# Name:         BM38.py
# Description:  在二叉树中找到两个节点的最近公共祖先
# Author:       PANG
# Date:         2022/7/12
# ----------------------------------------------
from typing import List


class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution:
    # 记录是否找到到o的路径
    flag = False

    # 求得根节点到目标节点的路径
    def dfs(self, root: TreeNode, path: List[int], o: int):
        if self.flag or not root:
            return
        path.append(root.val)
        # 节点值不同，可以直接用值比较
        if root.val == o:
            self.flag = True
            return
        # dfs遍历查找
        self.dfs(root.left, path, o)
        self.dfs(root.right, path, o)
        # 找到
        if self.flag:
            return
        # 该子树没有，回溯
        path.pop()

    def lowestCommonAncestor(self, root: TreeNode, o1: int, o2: int) -> int:
        path1, path2 = [], []
        # 求根节点到两个节点的路径
        self.dfs(root, path1, o1)
        # 重置flag， 查找下一个
        self.flag = False
        self.dfs(root, path2, o2)
        i = 0
        res = None
        while i < len(path1) and i < len(path2):
            if path1[i] == path2[i]:
                res = path1[i]
                i += 1
            else:
                break
        return res

复杂度分析

• 时间复杂度：O(n)，其中n为二叉树节点数，递归遍历二叉树每一个节点求路径，后续又遍历路径
• 空间复杂度：O(n)，最坏情况二叉树为链表，深度为n，递归栈深度和路径数组为n

方法2： 二叉树递归

1. 如果o1和o2中的任一个和root匹配，那么root就是最近公共祖先。
2. 如果都不匹配，则分别递归左、右子树。
3. 如果有一个节点出现在左子树，并且另一个节点出现在右子树，则root就是最近公共祖先
4. 如果两个节点都出现在左子树，则说明公共祖先在左子树中，否则在右子树
5. 继续递归左、右子树，直到遇到步骤1或步骤3的情况

class Solution:
    def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
        # 该子树没找到，返回-1
        if not root:
            return -1
        # 该节点是其中某一个节点
        if root.val == o1 or root.val == o2:
            return root.val
        # 左子树寻找公共祖先
        left = self.lowestCommonAncestor(root.left, o1, o2)
        # 右子树寻找公共祖先
        right = self.lowestCommonAncestor(root.right, o1, o2)
        # 如果左子树没有找到，则在右子树中
        if left == -1:
            return right
        # 如果右子树没找到，则在左子树中
        if right == -1:
            return left
        # 否则是当前节点
        return root.val