JZ86 在二叉树中找到两个节点的最近公共祖先

示例1

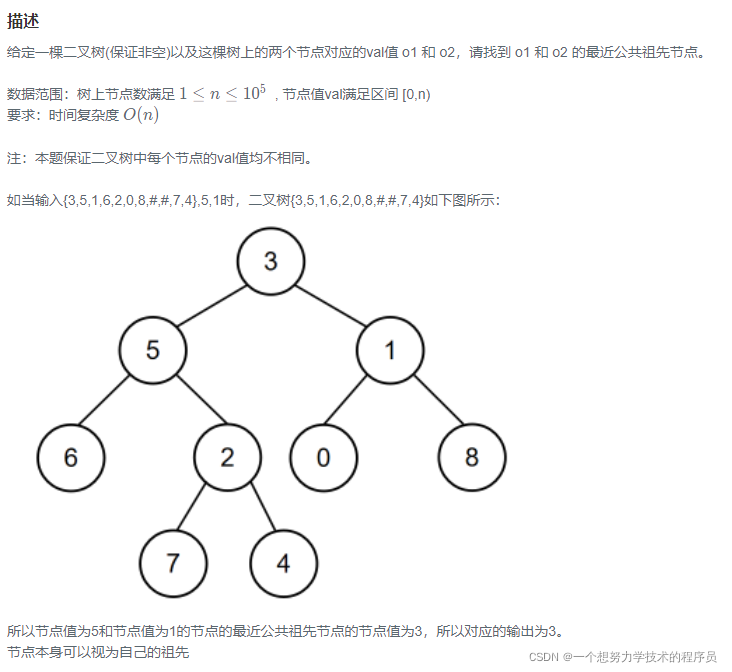
输入：{3,5,1,6,2,0,8,#,#,7,4},5,1

返回值：3

示例2

输入：{3,5,1,6,2,0,8,#,#,7,4},2,7

返回值：2

 第一种解法

使用递归解决，将每个节点的左子树，每个节点的右子树都当做一个新的完整的树，进行递归判断即可，判断逻辑为

* step 1：如果o1和o2中的任一个和root匹配，那么root就是最近公共祖先。

* step 2：如果都不匹配，则分别递归左、右子树。

* step 3：如果有一个节点出现在左子树，并且另一个节点出现在右子树，则root就是最近公共祖先.

* step 4：如果两个节点都出现在左子树，则说明最低公共祖先在左子树中，否则在右子树。

* step 5：继续递归左、右子树，直到遇到step1或者step3的情况。

public int firstLowestCommonAncestor (TreeNode<Integer> root, int o1, int o2) {
        if(null == root){
            return -1;
        }
        if(root.val == o1 || root.val == o2){
            return root.val;
        }
        int left = firstLowestCommonAncestor(root.left,o1,o2);
        int right = firstLowestCommonAncestor(root.right,o1,o2);
        if(left == -1){
            return right;
        }
        if(right == -1){
            return left;
        }
        return root.val;
    }

第二种解法

使用深度优先搜索算法，深度优先搜索一般用于树或者图的遍历，其他有分支的（如二维矩阵）也适用。它的原理是从初始点开始，一直沿着同一个分支遍历，直到该分支结束，然后回溯到上一级继续沿着一个分支走到底，如此往复，直到所有的节点都有被访问到。判断逻辑为

* step 1：利用dfs求得根节点到两个目标节点的路径：每次选择二叉树的一棵子树往下找，同时路径数组增加这个遍历的节点值。

* step 2：一旦遍历到了叶子节点也没有，则回溯到父节点，寻找其他路径，回溯时要去掉数组中刚刚加入的元素。

* step 3：然后遍历两条路径数组，依次比较元素值。

* step 4：找到两条路径第一个不相同的节点即是最近公共祖先。

 

boolean flag = false;
    public int secnodLowestCommonAncestor (TreeNode<Integer> root, int o1, int o2) {
        if(null == root){
            return -1;
        }
        List<Integer> listO1 = new ArrayList<>();
        List<Integer> listO2 = new ArrayList<>();
        dfs(root,o1,listO1);
        flag = false;
        dfs(root,o2,listO2);
        int result = 0;
        for (int i = 0; i < listO1.size() && i < listO2.size(); i++) {
            if(listO1.get(i).equals(listO2.get(i))){
                //可能存在多个公共祖先 最后一个相同的节点就是最近公共祖先
                result = listO1.get(i);
            }
        }
        return result;
    }


    public void dfs(TreeNode<Integer> root, int o, List<Integer> list){
        if(root == null || flag){
            return;
        }
        list.add(root.val);
        if(o == root.val){
            flag = true;
            return;
        }
        dfs(root.left,o,list);
        dfs(root.right,o,list);
        if(flag){
            return;
        }
        list.remove(list.size()-1);
    }