【剑指Offer】二叉树的下一个结点——两种解法

题目描述

给你一颗二叉树的一个结点，返回中序遍历顺序中这个结点的下一结点。二叉树不仅有左右孩子指针，还有指向父亲结点的指针。
结点类型如下：

public class TreeLinkNode {
    public int val;
    public TreeLinkNode left = null;
    public TreeLinkNode right = null;
    public TreeLinkNode next = null;

    public TreeLinkNode(int val) {
        this.val = val;
    }
}

解题思路

首先问自己一个问题，如果这道题出现在笔试题中，自己会用什么方法做？如果出现在面试题中呢？同一道题为什么还分出现在笔试题中还是面试题中呢？很显然，笔试题中只要能过就好，设计的算法丑点，慢点也无所畏，不一定需要最优解法，当然前提是能够通过。而面试中就不一样了，显然面试官希望听到最优解法。

方法1：暴力解法

直接模拟题意。题意需要找到某个结点中序遍历的下一个结点，那很显然可以这样：

1. 根据给出的结点求出整棵树的根节点
2. 根据根节点递归求出树的中序遍历，存入ArrayList中
3. 在ArrayList中查找当前结点，则当前结点的下一结点即为所求。

虽然有点暴力，但是时间复杂度也是线性的：
第一步：最坏为O(N)，N为整棵树结点的个数
第二步：O(N)
第三步：最坏为O(N)
所以整的时间复杂度：3*O(N)

时间复杂度还可以接受，关键是思路好想并且每一步的代码都很简单。代码如下：

import java.util.ArrayList;
public class Solution {
    ArrayList<TreeLinkNode> list = new ArrayList<>();
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        TreeLinkNode parrent = pNode;
        while (parrent.next!=null){
            parrent = parrent.next;
        }
        InOrder(parrent);
        for (int i = 0; i < list.size(); i++) {
            if (pNode==list.get(i)){
                return i==list.size()-1?null:list.get(i+1);
            }
        }
        return null;
    }

    private void InOrder(TreeLinkNode parrent) {
        if (parrent!=null){
            InOrder(parrent.left);
            list.add(parrent);
            InOrder(parrent.right);
        }
    }
}

时间复杂度为O(N)，空间复杂度为O(N)

方法2：最优解法

（1）分析
以如下二叉树为例，中序遍历为：{D,B,H,E,I,A,F,C,G}

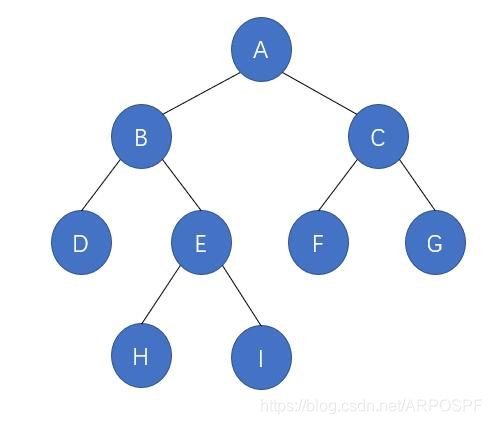
仔细观察，可以把中序下一结点归为几种类型：

• 有右子树，下一结点是右子树中的最左结点，例如 B，下一结点是 H
• 无右子树，且结点是该结点父结点的左子树，则下一结点是该结点的父结点，例如 H，下一结点是 E
• 无右子树，且结点是该结点父结点的右子树，则一直沿着父结点追朔，直到找到某个结点是其父结点的左子树，如果存在这样的结点，那么这个结点的父结点就是我们要找的下一结点。例如 I，下一结点是 A；例如 G，并没有符合情况的结点，所以 G 没有下一结点

代码如下：

public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        // 情况1
        if (pNode.right != null) {
            TreeLinkNode pRight = pNode.right;
            while (pRight.left != null) {
                pRight = pRight.left;
            }
            return pRight;
        }
        // 情况2
        if (pNode.next != null && pNode.next.left == pNode) {
            return pNode.next;
        }
        // 情况3
        if (pNode.next != null) {
            TreeLinkNode pNext = pNode.next;
            while (pNext.next != null && pNext.next.right == pNext) {
                pNext = pNext.next;
            }
            return pNext.next;
        }
        return null;
    }
}

时间复杂度为O(N)，空间复杂度为O(1)。