决策树快速入门：不仅有公式图解，还有能直接跑的分类+回归代码！

决策树是机器学习中最直观、最易理解的算法之一，像一棵“判断树”帮我们做分类或回归。今天从基础概念到代码实战，带新手快速入门，全程分点拆解，公式+案例+代码一步到位～

另外，我还整理了决策树经典论文+代码合集，需要的可以分享给你

➔➔➔➔点击查看原文，获取更多机器学习干货和资料！https://mp.weixin.qq.com/s/7tn-ga8C3HMz_phwQ_UIiA

一、决策树是什么？一句话讲清

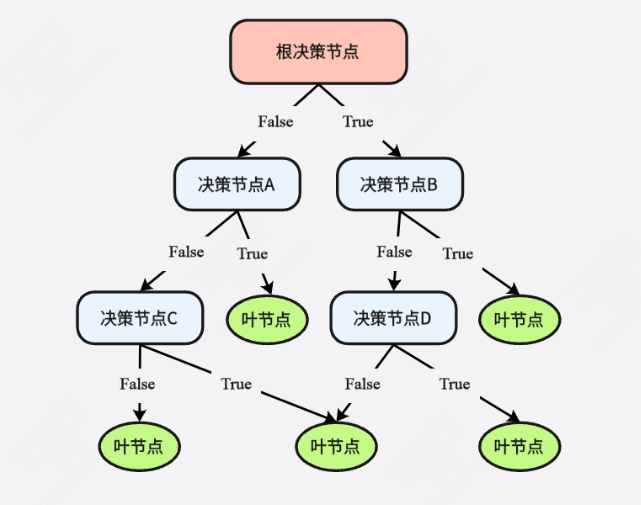
决策树（Decision Tree）是树形结构的预测模型，核心是把杂乱数据转化为“if-else”决策规则：

• 根节点：对分类/回归影响最大的属性（比如判断西瓜好坏时的“纹理”）

• 中间节点：属性判断条件（比如“纹理=清晰？”）

• 叶子节点：最终结果（比如“好瓜”“坏瓜”或回归的具体数值）

• 每条路径：一条完整决策规则（例：纹理清晰→触感硬滑→好瓜）

二、决策树怎么生成？3步核心流程

从“根节点”到“完整树”，遵循固定逻辑循环，流程如下：

1. 初始化：将所有训练数据放入根节点

2. 终止判断（满足任一条件则停止划分，标记为叶子节点）：

   • 数据为空：根节点返回null，中间节点标记为“样本最多的类别”

   • 所有样本属于同一类：直接标记为该类别

3. 最优划分（不满足终止条件时）：

   • 对当前节点的所有属性，计算“划分效果”（关键！下文详解）

   • 选“划分效果最好”的属性作为当前节点的判断条件

   • 按该属性的取值拆分数据，生成子节点，回到步骤2循环

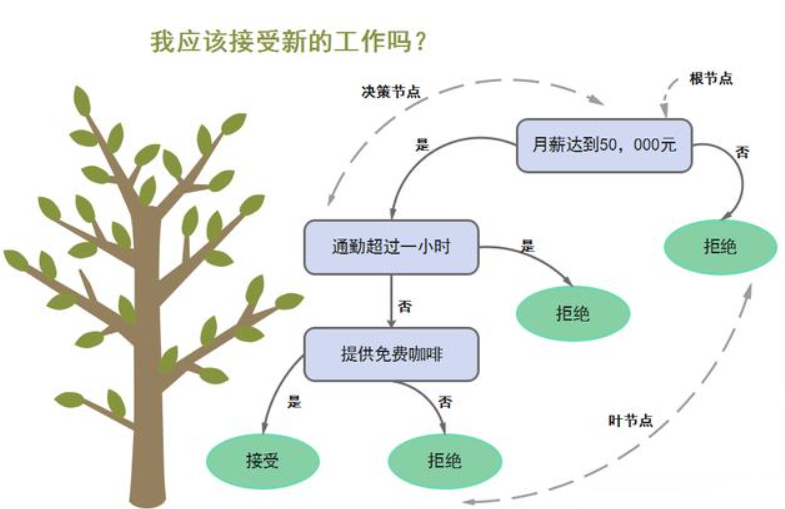
三、关键难点：如何选“最优划分属性”？3大准则

选属性的核心是“让划分后的数据更‘纯’”（比如同一子节点里尽量都是好瓜），常用3种准则：

3.1 信息增益（ID3算法用它）

先理解“信息熵”——描述数据的混乱程度：熵越大，数据越杂。

1）信息熵公式

假设样本集D有K个类别，第k类样本占比为（），则D的信息熵为：

• 例：二分类（好瓜/坏瓜），若好瓜占比0.5、坏瓜0.5，（最混乱）；若全是好瓜，（最纯净）。

2）信息增益公式

用属性a划分D后，得到v个子集，信息增益是“划分前熵 - 划分后加权熵”，值越大划分效果越好：

• ：子集的样本占比（权重）

• 例：用“纹理”划分西瓜数据，计算Gain(D,纹理)，再对比“色泽”“触感”的Gain，选最大的作为最优属性。

3.2 增益比（C4.5算法用它，解决信息增益的缺陷）

信息增益偏爱“取值多的属性”（比如“样本序号”，每个序号对应1个样本，划分后熵为0，Gain最大，但毫无意义）。
增益比通过除以“属性固有值IV(a)”矫正偏差：

1）属性固有值公式

• 属性a取值越多，IV(a)越大，从而抑制Gain的偏向性。

2）增益比公式

• C4.5逻辑：先选Gain高于平均值的属性，再在其中选Gain_ratio最大的。

3.3 基尼指数（CART算法用它，支持分类+回归）

基尼指数描述“随机抽2个样本，类别不同的概率”，值越小数据越纯：

1）基尼指数公式

• 例：二分类（p=0.5），²²（最混乱）；全是好瓜，（最纯净）。

2）划分后基尼指数

用属性a划分后，基尼指数为子集加权和，选“划分后基尼指数最小”的属性：

CART的特殊点：严格二叉树

ID3/C4.5一个属性可分多个子节点（如纹理→清晰/稍糊/模糊，3个子节点），但CART只能分2个（如纹理=清晰？是/否），同一属性可重复使用。

3.4 3种准则对比表

准则	对应算法	适用场景	优点	缺点
信息增益	ID3	分类	计算简单，直观	偏爱取值多的属性
增益比	C4.5	分类	矫正偏向性	偏爱取值少的属性
基尼指数	CART	分类/回归	计算快，支持二叉树	对噪声略敏感

四、防止过拟合：决策树的“剪枝”技巧

决策树天生容易“长太满”（把训练集噪声也学进去，测试集效果差），剪枝是关键：

1. 预剪枝：“提前刹车”

   • 时机：每次划分前先评估，若划分后测试集精度没提升，就停止划分，标记为叶子节点。

   • 优点：计算快，避免冗余节点；缺点：可能“欠拟合”（没学透）。

2. 后剪枝：“先长再剪”

   • 时机：先生成完整决策树，再从叶子往根遍历，若把某子树换成叶子节点后测试集精度提升，就剪去子树。

   • 优点：效果更好，泛化能力强；缺点：计算量大。

五、特殊数据处理：连续值+缺失值

实际数据不会完美，这两种情况要处理：

5.1 连续值（如西瓜含糖率0.1-0.9）：二分法离散化

1. 步骤：

   • 对连续属性a的取值排序：

   • 生成候选划分点：（共n-1个，取相邻值的中点）

   • 对每个，将数据分为“≤t_i”和“>t_i”两类，计算信息增益（或基尼指数）

   • 选增益最大的作为划分点，属性a可重复使用（如含糖率≤0.5？再分含糖率≤0.3？）

2. 连续值信息增益公式：

• ：≤t的样本；：>t的样本

5.2 缺失值（如部分西瓜没记录“触感”）：加权处理

1. 核心思路：只用水印缺失值的样本计算，再加权总样本占比。

2. 信息增益调整公式（ρ：无缺失值样本占比；：无缺失值样本中属性a取的占比）：

1. 样本划分：

   • 取值已知：正常划入对应子节点

   • 取值缺失：同时划入所有子节点，权重为样本原权重

六、决策树也能做回归？CART回归树

决策树不仅能分类（好瓜/坏瓜），还能回归（预测房价、温度），核心是CART回归树：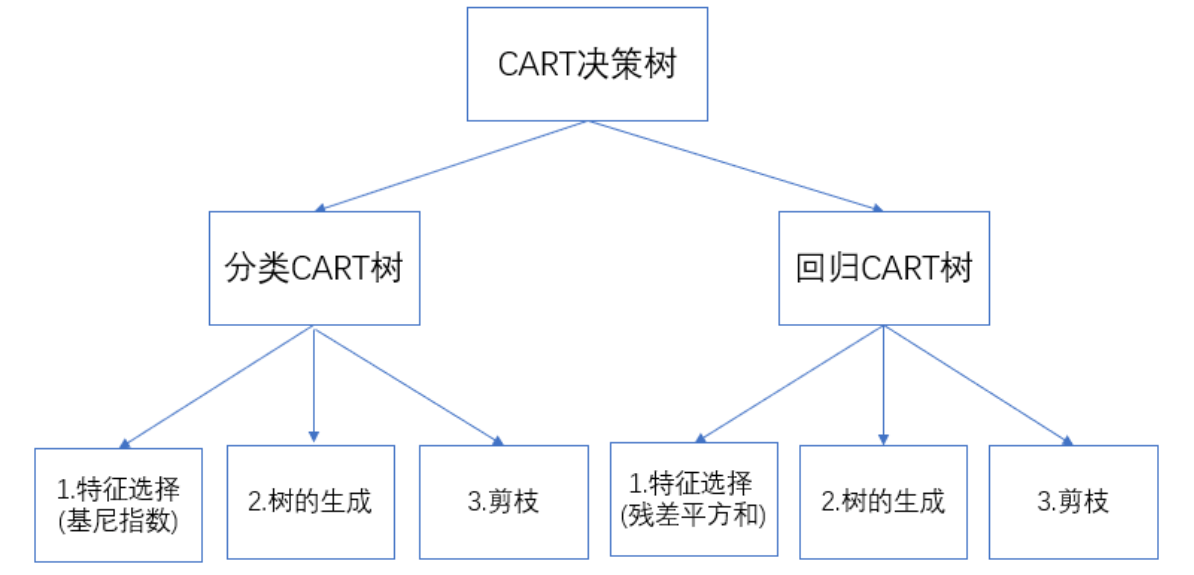

6.1 回归树流程

1. 初始化：所有数据放入根节点

2. 找最优划分点（j,s）：j是属性，s是属性j的取值，目标是“最小化误差平方和”

3. 划分数据：（）和（），子节点输出值为“该节点样本y的均值”

4. 终止判断：若子节点样本数≤阈值/树深达上限，停止；否则循环步骤2-3

6.2 最优划分点公式（最小二乘法）

对每个（j,s），计算误差平方和，选最小的（j,s）：

• ：的y均值；：的y均值（数学证明：均值能最小化误差平方和）

七、实战：用Python实现决策树（分类+回归）

用sklearn库，代码可直接运行，以“鸢尾花分类”和“波士顿房价回归”为例：

7.1 分类树代码（鸢尾花数据集）

# 1. 导入库和数据
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

# 加载数据（鸢尾花：3类花，4个特征）
data = load_iris()
X = data.data  # 特征：花萼长度、宽度，花瓣长度、宽度
y = data.target  # 标签：0/1/2（3种花）

# 2. 划分训练集/测试集（7:3）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42  # random_state固定划分，方便复现
)

# 3. 定义并训练决策树（用基尼指数，限制树深3）
clf = DecisionTreeClassifier(
    criterion="gini",  # 划分准则：gini/entropy
    max_depth=3,       # 最大树深（防止过拟合）
    random_state=42
)
clf.fit(X_train, y_train)  # 训练模型

# 4. 预测并评估
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"分类准确率：{accuracy:.2f}")  # 输出：分类准确率：1.00（效果超好）

# 5. 可视化决策树（可选，直观理解）
plt.figure(figsize=(10, 6))
plot_tree(clf, feature_names=data.feature_names, class_names=data.target_names, filled=True)
plt.show()

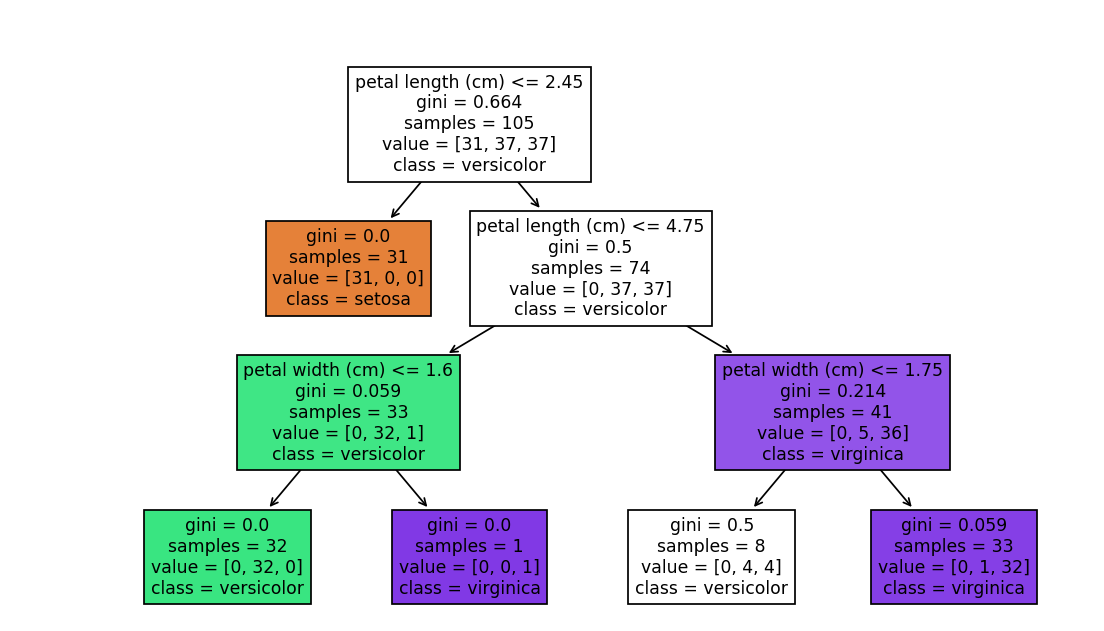
分类树代码（鸢尾花数据集）

7.2 回归树代码（波士顿房价数据集）

# 1. 导入库和数据
from sklearn.datasets import fetch_openml
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 正确显示负号

# 加载波士顿房价数据
boston = fetch_openml(name="boston", version=1)
X = boston.data  # 特征
y = boston.target.astype(float)  # 标签：房价中位数
feature_names = boston.feature_names  # 特征名称

# 2. 划分训练集/测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# 3. 定义并训练回归树
reg = DecisionTreeRegressor(
    criterion="squared_error",  # 回归准则：平方误差
    max_depth=4,                # 限制树深
    random_state=42
)
reg.fit(X_train, y_train)

# 4. 预测并评估
y_pred = reg.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print(f"回归RMSE：{rmse:.2f}")

# 5. 结果可视化
plt.figure(figsize=(15, 12))

# 子图1：实际值vs预测值
plt.subplot(2, 2, 1)
plt.scatter(y_test, y_pred, alpha=0.6)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--')  # 理想线：y=x
plt.xlabel('实际房价')
plt.ylabel('预测房价')
plt.title(f'实际值 vs 预测值 (RMSE: {rmse:.2f})')

# 子图2：误差分布直方图
plt.subplot(2, 2, 2)
errors = y_test - y_pred
sns.histplot(errors, kde=True)
plt.axvline(x=0, color='r', linestyle='--')
plt.xlabel('预测误差 (实际值-预测值)')
plt.ylabel('频数')
plt.title('预测误差分布')

# 子图3：特征重要性
plt.subplot(2, 2, 3)
importances = reg.feature_importances_
indices = np.argsort(importances)[::-1]  # 按重要性排序
plt.barh(range(len(indices)), importances[indices], color='b', alpha=0.7)
plt.yticks(range(len(indices)), [feature_names[i] for i in indices])
plt.xlabel('特征重要性')
plt.title('各特征对房价预测的重要性')

# 子图4：决策树结构可视化（简化版）
plt.subplot(2, 2, 4)
plot_tree(reg, feature_names=feature_names, filled=True, 
          rounded=True, fontsize=8, max_depth=2)  # 只显示前2层
plt.title('决策树结构（前2层）')

plt.tight_layout()
plt.show()

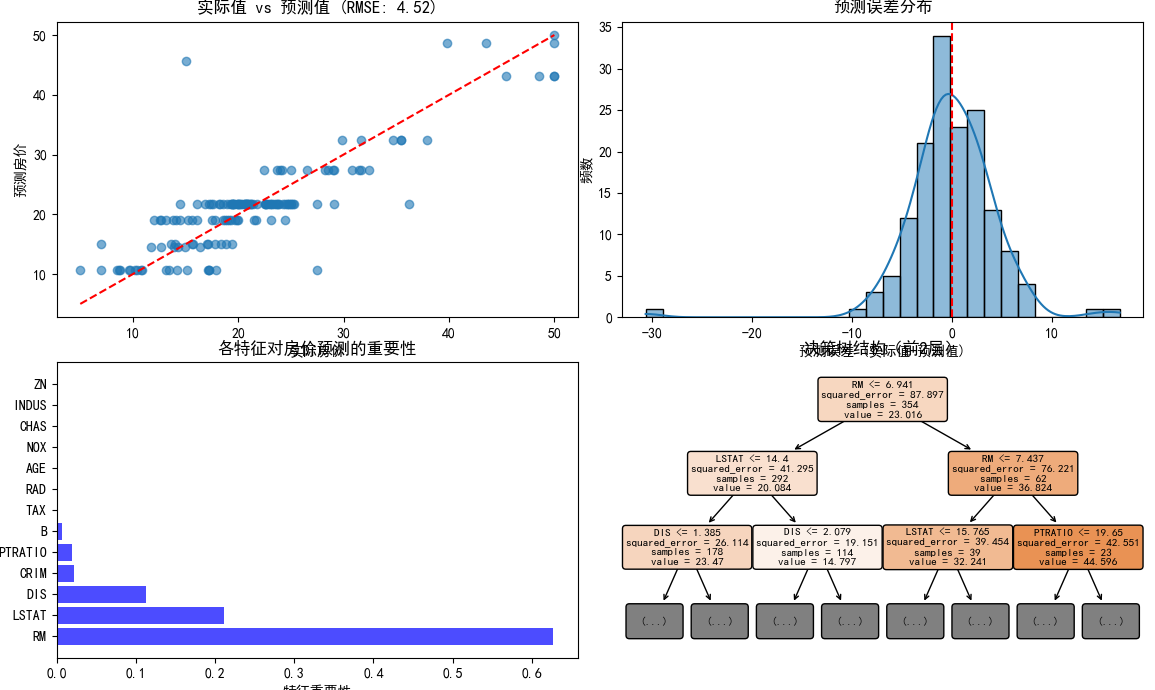
回归树结果

八、新手必看：sklearn参数调优重点

决策树的效果靠参数调优，这几个参数最关键：

参数	作用	常用值范围
criterion	划分准则（分类：gini/entropy；回归：squared_error）	分类默认gini，回归默认squared_error
max_depth	树的最大深度（防过拟合）	3-10（根据数据调整）
min_samples_split	划分节点的最小样本数（防过拟合）	2-10
min_samples_leaf	叶子节点的最小样本数（防过拟合）	1-5
random_state	固定随机种子（复现结果）	42/123（任意整数）

九、总结：新手入门决策树的3个关键点

1. 核心逻辑：用“树形结构”把数据转化为决策规则，关键是选“最优划分属性”

2. 算法差异：ID3（信息增益，分类）、C4.5（增益比，分类）、CART（基尼指数，分类+回归）

3. 实战技巧：用剪枝（max_depth）防过拟合，连续值需离散化，缺失值需加权处理

决策树是集成算法（随机森林、XGBoost）的基础，学好它能帮你理解更复杂的模型～ 赶紧把代码复制运行，动手试试吧！

➔➔➔➔点击查看原文，获取更多机器学习干货和资料！https://mp.weixin.qq.com/s/7tn-ga8C3HMz_phwQ_UIiA