K近邻法代码实现: https://blog.youkuaiyun.com/ACM_hades/article/details/89645095
一、K近邻算法:
- K近邻算法(KNN)是一种基本分类与回归方法,这里只讨论分类问题。
- K近邻算法的基本思想:给定一个训练数据集,对新输人的实例,在训练集中找到与该实例最近邻的 k k k个实例,这个 k k k个实例的多数属于某类,就把该实例分为这个类。
- 算法过程:
- 训练集: T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T=\{(x_1,y_1 ),(x_2,y_2 ),…,(x_N,y_N)\} T={(x1,y1),(x2,y2),…,(xN,yN)};其中: x i ∈ X ∈ R n x_i∈X∈R^n xi∈X∈Rn表示实例的特征向量, y i ∈ Y ∈ { c 1 , c 2 , … , c K } y_i∈Y∈\{c_1,c_2,…,c_K\} yi∈Y∈{c1,c2,…,cK}为实例类别。
- 预测新样例
x
x
x的类别
y
y
y的步骤:
- 根据给定的距离度量,在训练集 T T T中找出与 x x x最邻近的 k k k个点,这 k k k个点记为: N k ( x ) N_k (x) Nk(x)
- 在 N k ( x ) N_k (x) Nk(x)中根据分类决策规则(如:多数表决)决定 x x x的类别 y y y: y = max c j ∑ x i ∈ N k ( x ) I ( y i = c i ) y=\max_{c_j }∑_{x_i∈N_k (x)} I(y_i=c_i) y=cjmaxxi∈Nk(x)∑I(yi=ci)其中 I I I是指示函数。
二、K近邻模型的三要素:
- K近邻模型的三要素:距离度量、k值的选择和分类决策规则
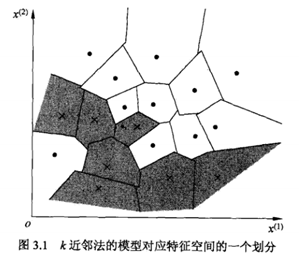
- K近邻算法的直观表示:
- 当训练集、距离度量、k值的选择和分类决策规则确定后,对任何一个新的输入实例他所属的类别是唯一确定的。这相当于在给定上述要素后,特征空间就被划分为一个个互不相交的子空间,并且子空间的类别是确定的。所有当一个新样本来了后我们的算法只是帮这个样本找到相应的子空间从而得到它的类别。
- 取k=1时,子空间的情况如下,每个子空间又叫做单元:
- 距离度量:
x
i
,
x
j
∈
X
∈
R
n
x_i,x_j∈X∈R^n
xi,xj∈X∈Rn
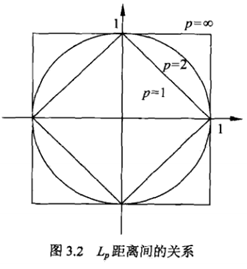
- L p L_p Lp距离: L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p L_p (x_i,x_j )=(∑_{l=1}^n|x_i^{(l) }-x_j^{(l) } |^p )^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣p)p1
- p = 2 p=2 p=2就是欧式空间: L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_2 (x_i,x_j )=(∑_{l=1}^n|x_i^{(l) }-x_j^{(l) } |^2 )^{\frac{1}{2}} L2(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣2)21
- p = 1 p=1 p=1就是曼哈顿距离: L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_1 (x_i,x_j )=∑_{l=1}^n|x_i^{(l) }-x_j^{(l) } | L1(xi,xj)=l=1∑n∣xi(l)−xj(l)∣
- p = ∞ p=∞ p=∞就是坐标距离的最大值: L 1 ( x i , x j ) = max l ∣ x i ( l ) − x j ( l ) ∣ L_1 (x_i,x_j )=\max_l|x_i^{(l) }-x_j^{(l) } | L1(xi,xj)=lmax∣xi(l)−xj(l)∣
- 在二维空间与原点的L_p距离为1的点的形状:
- k值的选择:
- k较小时:近似误差会减少,这样只有与输入实例较近的训练实例会对预测结果起作用。但是估计误差会变大,这倒是预测结果对近邻实例非常敏感。总的来说k越小模型越复杂,越容易发生过拟合。
- k越大:但是估计误差会变小,近似误差会变大。这样只有与输入实例较远的训练实例会对预测结果起作用,可能会使预测发生错误。总的来说k越大模型越简单。
- 在应用中k值一般取一个较小的值,通常采用交叉验证法来选取最优的k。
- 分类决策规则:
- 一般采用多数表决法。
三、K近邻的实现方法:Kd树
- Kd树:是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。它是一颗二叉树,它表示对k维空间的一个划分。
- 构造Kd树:书上的构造kd树的过程说的过于复杂,这里我从算法角度来讲解该过程。
- Kd树是一颗二叉树,树的每一层对应着k为空间的每个维度,树的第j层对应的维度是l=j%k.
- 树中每节点对应着一种划分:下面我们演算树中某一个节点的划分过程。
- 假设该节点在树中的第 j j j层,则对应的维度就是 l = j l=j%k l=j,它包含的节点集: T ′ = { ( x 1 ′ , y 1 ′ ) , ( x 2 ′ , y 2 ′ ) , … , ( x h ′ , y h ′ ) } T'=\{(x_1',y_1' ),(x_2',y_2' ),…,(x_h',y_h' )\} T′={(x1′,y1′),(x2′,y2′),…,(xh′,yh′)}其中 x i ′ ∈ R k x_i'∈R^k xi′∈Rk;我们将该节点包含的所有样本点 [ x 1 ′ , x 2 ′ , … , x h ′ ] [x_1',x_2',…,x_h'] [x1′,x2′,…,xh′]的第l维度的值取出 [ x 1 ( l ) ′ , x 2 ( l ) ′ , … , x h ( l ) ′ ] [x_1^{(l)'},x_2^{(l)'},…,x_h^{(l)'}] [x1(l)′,x2(l)′,…,xh(l)′],并进行排序,找到找到其中的中位数(单个样本点),以这个中位数划分点将样本集 T ′ T' T′进行划分
- 我们将中位数的样本点保存到该节点,并生成左右两个子节点分别包含中位数之前和中位数之后的子集。
- 然后对左右子节点进行递归。直到节点不包含任何样本结束。
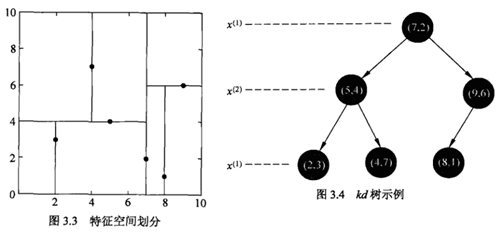
- 根节点包含所有样本集。即对所有样本在第一个维度进行划分。
- 对于二维空间中的数据集
T
=
{
(
2
,
3
)
,
(
5
,
4
)
,
(
9
,
6
)
,
(
4
,
7
)
,
(
8
,
1
)
,
(
7
,
2
)
}
T=\{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\}
T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},形成的
k
d
kd
kd树如下:
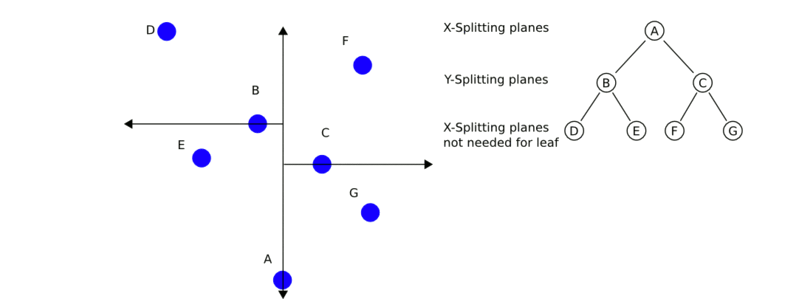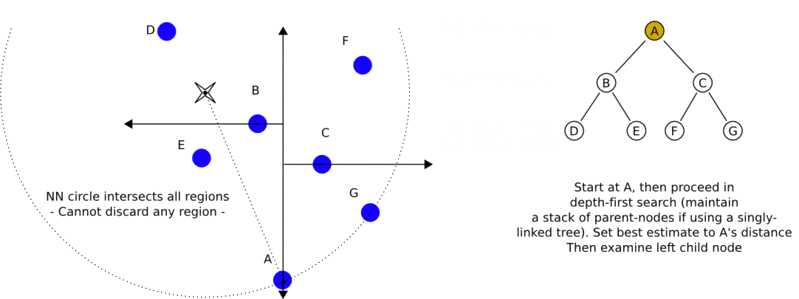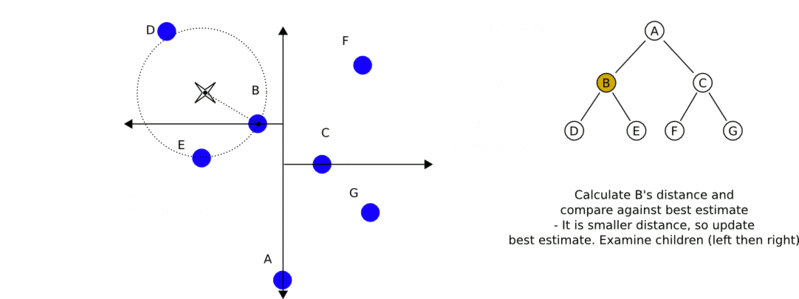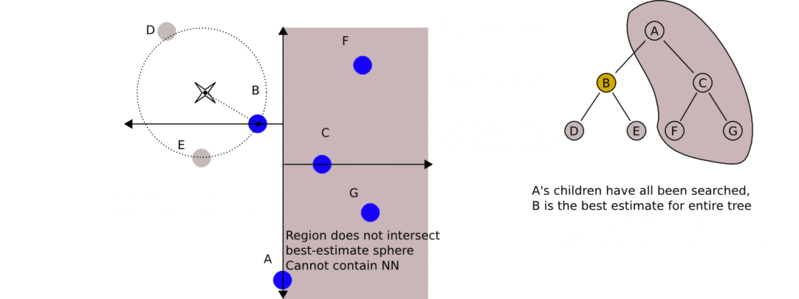
- 最近邻搜索:
- 给定一个输入实例,首先找到包含输入实例的叶节点。然后从该叶节点出发,依次回退到父节点。不断查找与输入实例最近邻的节点,当不存在距离更小的节点时终止搜索
- 输入实例与其最近邻样本点形成的超球体的内部一定没有其他样本点。基于这种性质,最近邻搜索算法如下:
- 从根节点出发,找到包含输入实例的叶节点,即若输入实例当前维的坐标小于切分点的坐标,移动到左子节点,否则移动到右子节点,直到到达叶节点为止,并将当前叶节点作为“当前最近点”;
- 递归地向上回退,对每个节点执行以下操作:
- a. 若该节点保存的实例比"当前最近点"距离输入实例更近,则将该实例作为"当前最近点";
- b. "当前最近点"一定存在于该节点一个子节点对应的区域,检查该子节点的兄弟节点对应区域是否有更近的点。即若"当前最近点"与输入实例形成的超球体与"当前最近点"的父节点的分割超平面相交,则"当前最近点"的兄弟节点可能含有更近的点,此时将该兄弟节点作为根节点一样,执行步骤1。若不相交,则向上回退。
- 当回退到根节点时,搜索结束。最后的"当前最近点",即为输入实例的最近邻点。
- 下面是一个动态的过程图:
- Kd树总结:
- 通过实验发现kd树算法并不适合所有数据,我使MNIST数据集进行实验发现比直接算还要慢,经过调试发现,每个测试样本点都遍历完了整个kd树。这可能是数据本身性质造成
- Kd树只适合欧式距离,应该为它用了:输入实例与其最近邻样本点形成的超球体的内部一定没有其他样本点,这个性质,即超球体。




 本文深入探讨了K近邻算法的原理与应用,包括算法的基本思想、过程、模型的三要素,以及Kd树实现方法。阐述了距离度量、k值选择和分类决策规则的重要性,并介绍了Kd树的构造和最近邻搜索算法。
本文深入探讨了K近邻算法的原理与应用,包括算法的基本思想、过程、模型的三要素,以及Kd树实现方法。阐述了距离度量、k值选择和分类决策规则的重要性,并介绍了Kd树的构造和最近邻搜索算法。
















 1042
1042

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








