Character-Aware Neural Language Models

参考链接

参考论文:https://arxiv.org/pdf/1508.06615v4.pdf

模型架构

整体架构图

• 说明：
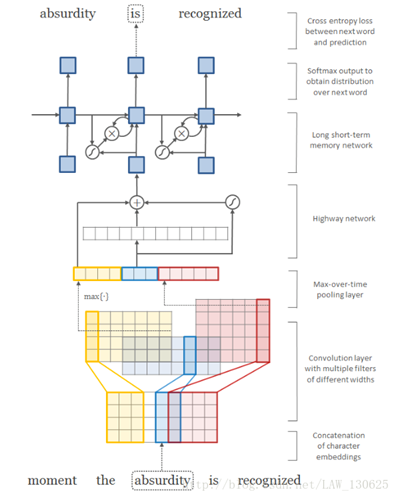
  • 该图描述的是一个典序的语言模型，当前的输入词是absurdity，预测词是is。
  • 第一步：查找character embeddings得到absurdity个字符的向量（维度为4），并将这些向量拼接成一个词矩阵$C^k$.
  • 第二步：将包含多个过滤器的卷积神经网络作用到矩阵$C^k$上，过滤器的个数为12个：3个大小为2的(蓝色)，4个大小为3的(黄色)，5个大小为4的(红色)。
  • 第三步：应用最大池化层，获取固定维度的词向量表示。
  • 第四步：使用highway network作用在上面输出的固定维度的向量。
  • 第五步：将highway network的输出作为多层的LSTM-RNN的输入。
  • 第六步：将LSTM-RNN中最顶层的输出喂到最后的全连接层+softmax层得到下一个词的概率分布。

循环神经网络(Recurrent Neural Network)

• 一般RNN的计算公式如下：$$h_t=f(W\ast x_t+U\ast h_{t-1}+b)$$其中$W$和$U$为模型参数，$x_t$为当前位置的词向量，$h_{(}t-1)$是上一时刻的隐藏层状态。理论上，RNN可以用隐藏状态$h_t$汇总从开始到时间$t$的所有历史信息。但是实际上，由于消失/爆炸的梯度，学习远程依赖信息是困难的。
• LSTM-RNN解决了学习长距离依赖关系的信息的问题，通过在RNN中增加一个记忆单元$c_t$。具体计算公式如下：$$i_t=\sigma (W^i{x}_t+U^i{h}_{t-1}+b^i)$$$$f_t=\sigma (W^f{x}_t+U^f{h}_{t-1}+b^f)$$$$o_t=\sigma (W^o{x}_t+U^o{h}_{t-1}+b^o)$$$$g_t=tanh(W^g{x}_t+U^g{h}_{t-1}+b^g)$$$$c_t=f_t\ast c_{t-1}+i_t\ast g_t$$$$h_t=o_t\ast tanh(c_t)$$$\sigma (\cdot )$和$tanh(\cdot )$是族元素的sigmoid函数和双曲正切函数。$\ast$是逐点乘积
• LSTM中的$c_t$缓解梯度消失的问题但是梯度爆炸依然存在。通过简单的梯度优化操作（gradient clipping）能够很好的解决这个问题。

字符级卷积神经网络(Character-level Convolutional Neural Network)

• 假定$C$表示字符表，$V$为词汇表，$Q\in R^{d\times |C|}$为字符向量矩阵，$k$为词汇表$V$中的一个词，$k$由字符$[c_1,c_2,\dots ,c_l]组成$长度为$l$，则词经过$Q$可以表示为矩阵$C^k\in R^{d\times l}.H\in R^{d\times w}$为过滤器，其中$w$为过滤器宽度，$f^k$为卷积层的输出，其计算公式：$$f^k[i]=tanh(<C^k[\ast ,i:i+w-1],H>+b)$$$<A,B>$表示A和B的Frobenius内积。$$<A,B{>}_F=\sum _{i,j}\overline{A_{i,j}}\ast B_{i,j}=tr(\overline{A}\ast B^T)$$其中$\overline{A_{i,j}}$表示复数的共轭数（将复数部分的符号取反），$\ast$表示内积，$tr$矩阵的迹。
  注意：当A，B为实数矩阵式，其结果就是对应元素相乘再求和
• 由上面公式我们可以看出来$f^k$是一个向量长度为：$l-w+1$.所以卷积层的输出$f$就是一个矩阵长度为12(12个过滤器).则卷积层后面的最大池化层公式为：$$y^k=\underset{i}{\max }(f^k[i])$$由公式可知y是一个长度为12的向量。

Highway Network

• 我们可以直接将最大池化层是输出向量$y$作为词向量了输入到LSTM-RNN中，也可以得到一个不错的性能。但是我们将$y$再经过一个多层的全连接层再输入到LSTM-RNN确发现效果变得更差。
• 在最大池化层加上一个highway network可以改善模型性能，highway network的公式如下：$$Z=t\ast g(W_H+b_H)+(1-t)\ast y$$$$t=\sigma (W_{T}y+b_T)$$注意:y和z的形状必须相同所以W_T,W_T必须是方正