【算法考核】--力扣 4.24

125.验证回文串

1. 输入的字符串s中可能有除了字母和数字之外的字符，所以先遍历字符串，将所有的字母和数字存进新的字符串str中

2. str中的字母可能有大写和小写，将str中所有大写字母转换成小写

3. 之后利用双指针，从字符串的开始 left 到结尾 right 进行比较
   如果有不同的字符，就不是回文字符串
   如果比较到最后，是回文字符串

//把所有字母都转成小写
void shift(char* str)
{
    int len = strlen(str);
    for(int i = 0; i < len; i ++ )
    {
        if(str[i] >= 'A' && str[i] <= 'Z')
        {
            str[i] = str[i] - 'A' + 'a';
        }
    }
}

bool isPalindrome(char* s) {
    int len = strlen(s);
    int capacity = 2 * pow(10,5);
    char* str = (char*)malloc(sizeof(char) * capacity);
    int j = 0 ;
    for(int i = 0; i < len; i ++ )
    {
        if((s[i] >= 'A' && s[i] <= 'Z') || (s[i] >= 'a' && s[i] <= 'z') || (s[i] >= '0' && s[i] <= '9'))
        {
            str[j++] = s[i];//所有字母和数字加到str中
        }
    }
    str[j] = '\0';//结束标志
    shift(str);
    
    int left = 0;
    int right = j-1;
    while(left < right)
    {
        if(str[left] != str[right])
        {
            return false;
        }
        left++;
        right--;
    }
    //走到这，说明没有不一样的字符
    return true;   
}

---

455.分发饼干

涉及贪心算法

思路是先满足胃口比较小的孩子，并且尽可能地使用尺寸小的饼干
也就是说 要给孩子能满足其胃口的 尺寸最小的饼干

但是这个题比较简单 ，直接对两个数组进行排序，然后从胃口最小的孩子开始，判断饼干是否能满足孩子
如果能，孩子和饼干都向后遍历
如果不能，饼干向后遍历，直到可以满足孩子胃口

在这个过程中，饼干和孩子都不可以越界

int cmp(const void* x, const void* y)
{
    return *(int*)x - *(int*)y;//升序
}

//

int findContentChildren(int* g, int gSize, int* s, int sSize) 
{
    //排序
    qsort(g, gSize, sizeof(int), cmp);
    qsort(s, sSize, sizeof(int), cmp);
    
    int cnt = 0;//记录数量
    //从胃口最小的孩子开始
    
    int min = gSize<sSize ?gSize :sSize;//小的值
    
    int i = 0;//孩子
    int j = 0;//饼干
    
    while(i < gSize && j < sSize)//保证不越界
    {
        if(g[i] <= s[j])//可以满足
        {
            cnt ++ ;
            i++;
            j++;
        }
        else //找尺寸更大的饼干
        {
            j++;
        }
    }
    return cnt;
}

---

226.反转二叉树

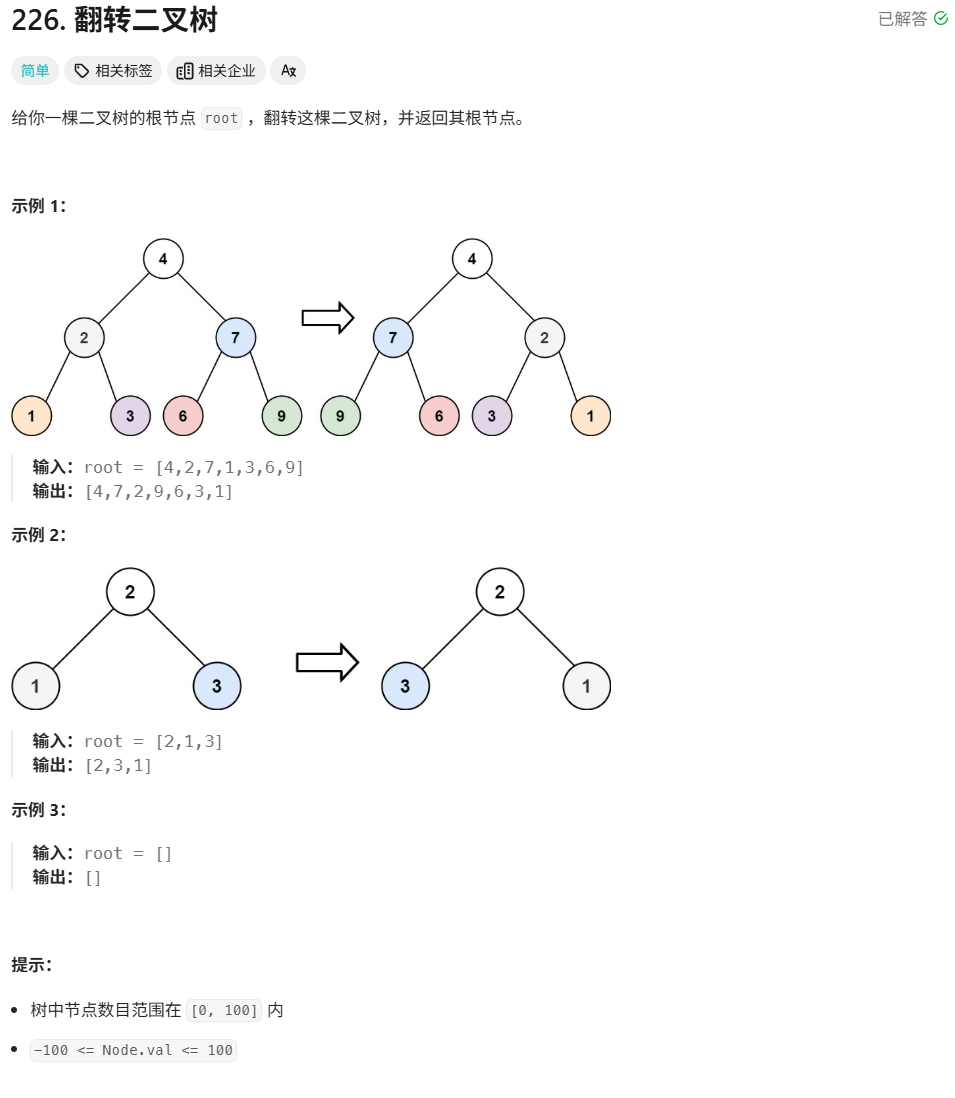
用递归来解决

因为每一个结点R是指针类型，交换了两个结点A、B，也就是交换了这个结点R的左右子树
就是A、B下面带着的一堆结点都交换过去了

根结点为空直接返回
根结点不为空

1. 交换根结点的左右子树
2. 之后交换左孩子的左右子树 和 右孩子的左右子树

------也就是对根结点的左右子树进行翻转操作

之后一直重复这个步骤，直到叶子节点

所以这个是递归的过程

typedef struct TreeNode TNode;


void shift(TNode* root)
{
    
    if(root == NULL)
    {
        return ;
    }
    
    //翻转
    TNode* left = root->right;
    TNode* right = root->left;
    
    root->left = left;
    root->right = right;
    
    //翻转左右子树
    shift(root->left);
    shift(root->right);
}


struct TreeNode* invertTree(struct TreeNode* root) 
{
    if(root == NULL)
    {
        return NULL;
    }
    
    //反转左右子树
    shift(root);
    
    return root;
    
}

---

19.删除链表的倒数第N个结点

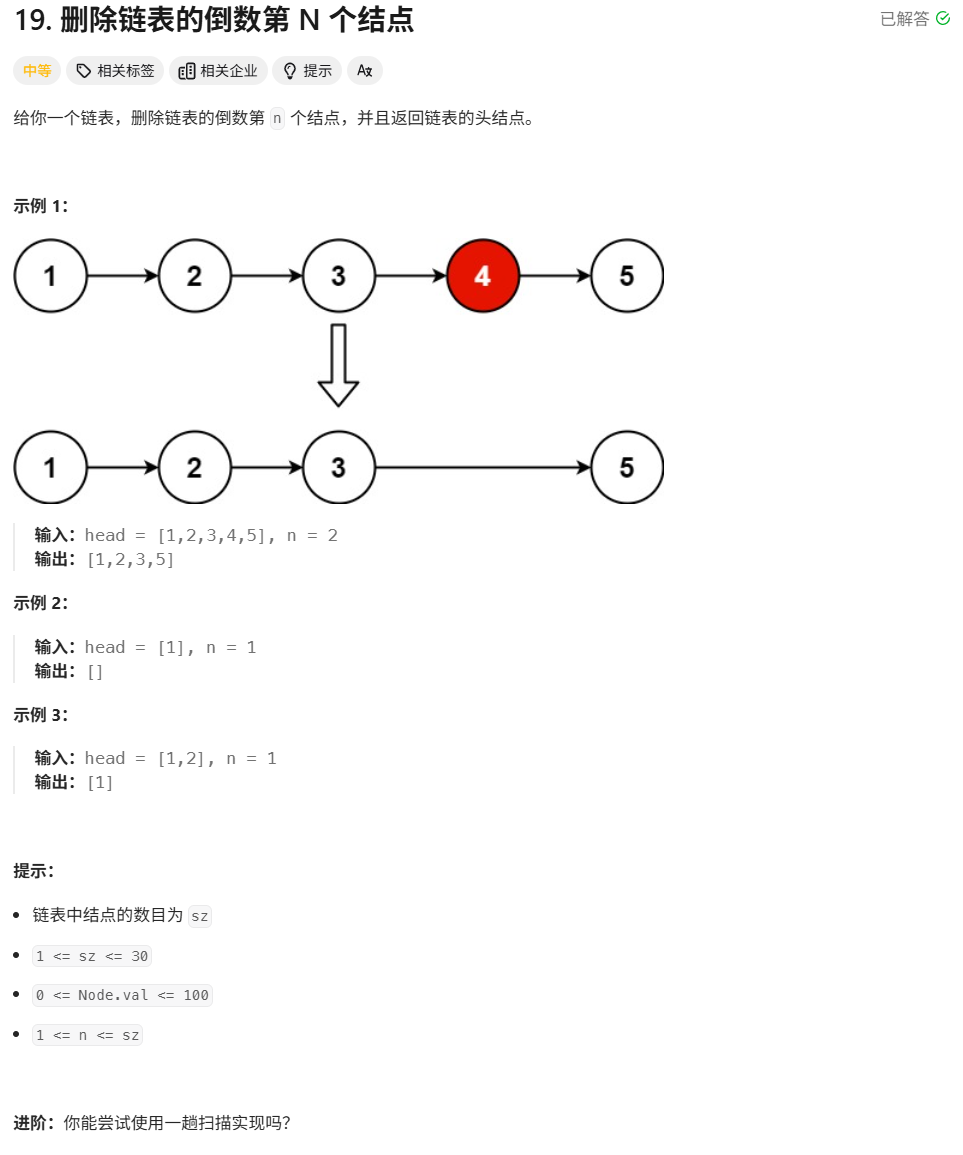
如果两个数开始的距离是distance，对这两个数同时加一，重复n次之后，这两个数还是差distance
倒数第n个结点和最后一个结点的距离是n-1，所以如果一个结点p1为头结点，p2是头结点向后
n-1个，那么p1、p2同时向后走，p2走到最后一个结点时，p1也就走到了倒数第N个结点

这样还需要记录p1结点的前一个结点

所以直接让p1从头结点的前一个开始，p2从头结点开始向后走n步，之后p1、p2向后，p2为空时，p1就是要删除的结点的前一个结点

typedef struct ListNode ListNode;

struct ListNode* removeNthFromEnd(struct ListNode* head, int n) 
{
    //要删除结点的前一个
    //一个指向头结点的指针向后 一个从头结点开始的指针向后到链表结尾
    ListNode* pcur = head;
    ListNode* prev = (ListNode*)malloc(sizeof(ListNode));
    prev->next = head;
    while(n--)
    {
        pcur = pcur->next;
    }
    
    if(pcur == NULL)
    {
        ListNode* nhead = head->next;
        //free(head);
        head = nhead;
        return head;
    }
    while(pcur)
    {
        prev = prev->next;
        pcur = pcur->next;
    }
    prev->next = prev->next->next;
    ListNode* del = prev->next;
    //free(del);
    del = NULL;
    
    return head;
}

---

921.使括号有效的最少添加

一开始看这题没看懂，以为题目给的示例“(())))”就是一个有效的字符串

这道题和力扣20.有效的括号很像
我前面的博客栈和队列写了有效的括号

说白了就是给左括号找右括号，给右括号找左括号，找不到加一个就好了

因为右括号是和 与它最近的并且没有相匹配的右括号 的左括号配对，所以对于每一个右括号，要找后出现的左括号，那问题是这个左括号怎么找

总不能再一个一个向前遍历找到左括号吧，并且这个左括号必须是没有与右括号进行配对的

所以要是能把没有进行配对过的左括号存起来就好了，如果存了很多左括号，遍历到了右括号，要找与它最近的左括号，也就是要找出最后存进去的左括号

后进先出，所以想到了栈

如果遍历到左括号就入栈
如果遍历到右括号，就判断栈中是否有左括号，有就出栈，没有就加一

（但是这个题好像并没有这么复杂，因为只有左右小括号，没有中括号大括号什么的，也就不用考虑存进左括号的顺序了吧？下面的代码是按上面的思路写的）

//用栈
int minAddToMakeValid(char* s) 
{
    //如果是空字符串 直接返回 
    if(*s == '\0')
    {
        return 0;
    }
    
    int len = strlen(s);
    
    char* stack = (char*)malloc(sizeof(char) * (len+1));//用数组模拟栈
    int top = 0;//栈顶
    int cnt = 0;//记录要添加的括号
    
    int i = 0;
    while(s[i] != '\0')
    {
        //左括号入栈
        if(s[i] == '(')
        {
            stack[top++] = s[i];
        }
        //右括号
        else 
        {
            if(top > 0)
            {
                top--;
            }
            else 
            {
                cnt ++ ;
            }
        }
        i ++ ;
    }
    
    //遍历到最后如果栈不为空 说明有多出的左括号 需要加右括号进行匹配
    while(top--)
    {
        cnt++;
    }
    return cnt; 
}

---

107.二叉树的层序遍历

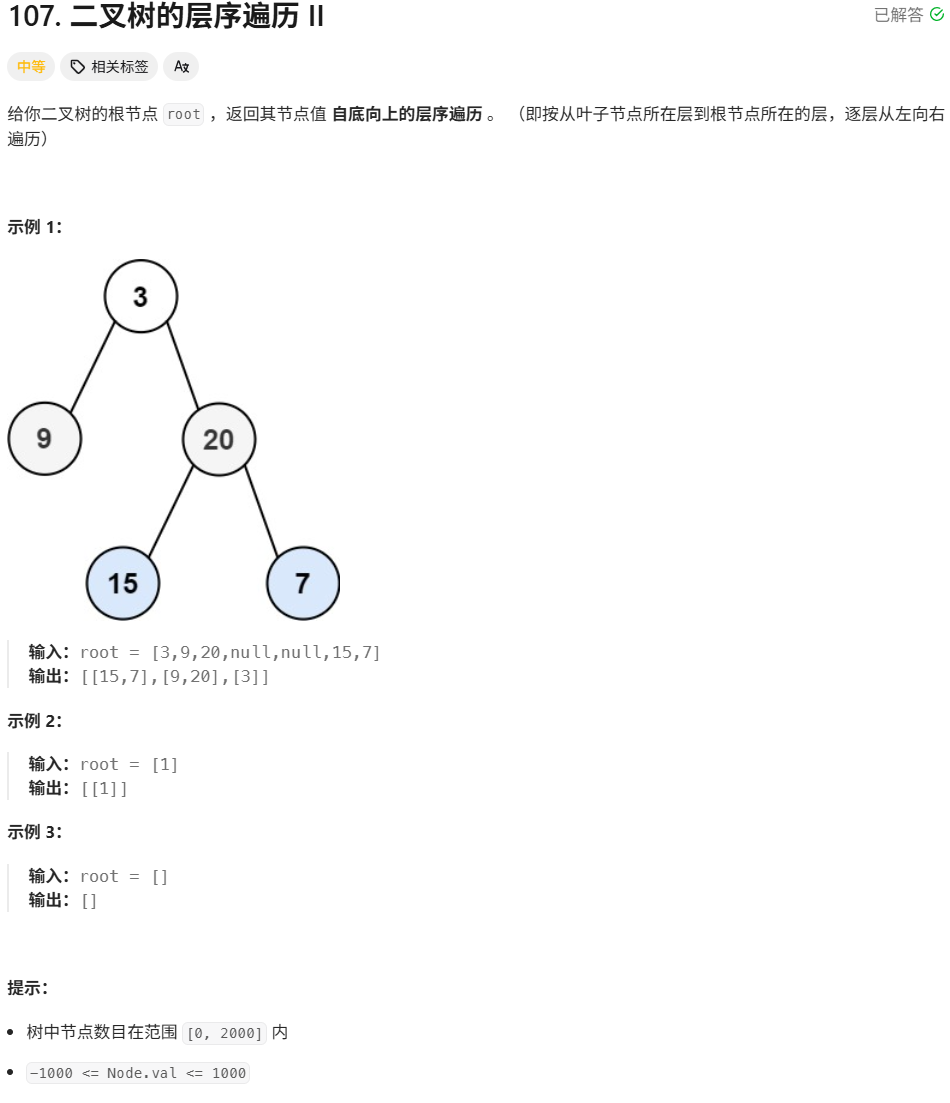
因为访问二叉树是根结点开始的，所以可以先进行自上向下的层序遍历，得到数组ret，然后反转数组ret

利用队列
定义一个返回数组ret，模拟队列
用front和back记录当前队头和队尾的位置
那么每一层的长度 len = back - front

先将根结点入队
接着 遍历二叉树的每一层（长度为len是循环条件）
遍历本层中的每一个结点
先将结点出队，存入返回数组ret，然后将元素的左右孩子入队（为空不存）
（出队不是进行删除操作，队头front增加后直接忽略了这个结点）

直到 front = back（队头等于队尾），表示所有层遍历完成

此时得到了自上向下的遍历结果

之后反转数组ret

typedef struct TreeNode TNode;

int** levelOrderBottom(struct TreeNode* root, int* returnSize, int** returnColumnSizes) 
{
    *returnSize = 0;
    int** ret = (int**)malloc(sizeof(int*) * 2000);//返回数组 
    *returnColumnSizes = (int*)malloc(sizeof(int) * 2000);//一次解引用得到的是层数 层数最多是2000
    if(!root)//如果根结点为空 直接返回
    {
        return ret;
    }
    
    TNode** queue = (TNode**)malloc(sizeof(TNode*) * 2000);//模拟队列 存储TNode*的数组
    
    //最初队头队尾都是0
    int front = 0;
    int back = 0;
    //将头结点加入队列
    queue[back++] = root;
    
    while(front < back)//如果队头等于队尾 遍历完成 终止
    {
        int len = back - front;//本层的结点个数
        int start = front;
        front = back;//此时front是下一层的开始
        //为返回数组开辟空间 
        ret[*returnSize] = (int*)malloc(sizeof(int) * len);
        
        for(int i = start; i < front; i ++ )
        {
            ret[*returnSize][i - start] = queue[i]->val;
            //左右孩子入队列
            if(queue[i]->left)
            {
                queue[back++] = queue[i]->left;
            }
            if(queue[i]->right)
            {
                queue[back++] = queue[i]->right;
            }
        }
        (*returnColumnSizes)[(*returnSize) ++ ] = len;
    }
    
    
    //反转二维数组
    for(int i = 0; i < (*returnSize)/2; i ++ )
    {
        int* tmp = (int*)malloc(sizeof(int) * (*returnColumnSizes)[i]);//开辟一维数组空间
        tmp = ret[i];
        ret[i] = ret[(*returnSize) - i - 1];
        ret[(*returnSize) - 1 -i] = tmp;
        
        //反转returnColumnSize
        int t = (*returnColumnSizes)[i];
        (*returnColumnSizes)[i] = (*returnColumnSizes)[(*returnSize) - 1 - i];
        (*returnColumnSizes)[(*returnSize) - 1 - i] = t;
    }
    return ret;
}

---

611.有效三角形的个数

有效三角形：两边之和大于第三边

如果有三角形三条边a、b、c
判断这个三角形是否有效，需要判断是否满足 a+b>c、b+c>a、a+c>b
这样进行三次比较很麻烦，如果能知道这个三角形最长的一条边max，那么只需要判断另外两条边之和是否大于max即可

用这个思想，对数组进行排序，从最大的值开始，找能和这个值组成三角形的边的个数，既减少了判断，也做到了不重不漏

假如这个最大值的下标是k，另外两条边的下标分别为left、right，并且这三个数从小到大依次是nums[left], nums[right], nums[k]

对于某一个k
为了做到不重不漏，让 left = 0，right = k - 1
判断是否满足有效三角形的要求
如果不满足，nums[left] + nums[right] < nums[k]，left++，找更大的数，进行判断
如果满足，nums[left] + nums[right ] > nums[k]，那么left再增大，nums[left]变大，始终满足
nums[left] + nums[right] > nums[k]，所以有right - left个数满足要求，之后right–再找有效三角形

//排序
int cmp(const void* a,const void* b)
{
    return *(int*)a-*(int*)b;
}

int triangleNumber(int* nums, int numsSize) 
{
    qsort(nums,numsSize,sizeof(int),cmp);//升序
    int count=0;

    //从最后一个元素开始遍历
    for(int k = numsSize-1; k >= 2; k -- )
    {
        int left = 0;//最小的
        int right = k-1;//中间
        while(left < right)
        {
            if(nums[left] + nums[right] > nums[k])//可以构成三角形 减小中间的数 
            {
                count += right - left;
                right -- ;
            }
            else//两边之和小于第三边 最小数 ++ 
            {
                left ++ ;
            }
        }
    }
    
    return count;
}

---

402.移掉K位数字

对于两个数字123a和123b，判断这两个数字的大小，判断a和b的大小就可以

所以如果想让一个数字最小，让它每一位上的数字都最小就可以
这道题用单调栈

如果此时已经有了两个数字24，分下面三种情况：
下一个数字是1，1比4要小，4出栈，1比2也要小，2也出栈，最后1入栈
下一个数字是3，3比4要小，4出栈，3比2要大，3直接入栈
下一个数字是5，5比4要大，5直接入栈

所以思路就是，先遍历字符串，遇到比栈顶元素大的直接入栈，
遇到比栈顶元素小的，先出栈，直到栈顶元素小于该元素或者栈顶没有元素，再入栈
如果栈为空，并且遇到了0，那不入栈 – 排除前置0

出栈的元素就是删除的元素，删除的元素不可以超过K个，如果超过K个了，直接将新元素入栈，不进行比较

如果遍历完字符串，删除的元素不够K个，那就直接从栈顶删除元素（栈中的元素是从小到大排列的，栈顶的元素必然最大）

如果最后栈为空，说明删除后是0，添加一个0

char* removeKdigits(char* num, int k) 
{
    int len = strlen(num);

    char* stack = (char*)malloc(sizeof(char) * (len+1));//用数组模拟栈
    int top = 0;//栈顶
    
    
    for(int i = 0; i < len; i ++ )
    {
        //如果新元素比栈顶元素小 出栈 
        while(top > 0 && num[i] < stack[top-1] && k > 0)//最多移除k个元素不能再多
        {
            top--;
            k--;
        }
        
        //新元素入栈 并且排除前导0的情况
        if(num[i] != '0' || top>0)
        {
            stack[top++] = num[i];
        }
    }

    //如果删除的元素不够多 //1 2 3 4 5 6
    //在栈顶进行删除 因为栈顶的元素比下面的都大
    while(k > 0 && top > 0)//保证栈不为空
    {
        top--;
        k--;
    }
    if(top == 0)//栈为空 添加数字0
    {
        stack[top++] = '0';
    }
    stack[top++] = '\0';//手动添加结束标志

    return stack;
}