目录
1. 使用数组,求出右边数列的前20项:1,2,1,3,2,5,3,8·····。
3.C语言对一维数据(假设有N个)进行排序,试分析最多需要对换元素的次数,何时会出现这种情况?
一.实验目的:
1.掌握一维数组的使用方法
2.掌握二维数组的使用方法
二.实验内容
1. 使用数组,求出右边数列的前20项:1,2,1,3,2,5,3,8·····。
分析:
这个问题可以通过动态规划解决。首先,定义两个数组,其中an1[10]表示数列的奇数项,an2[10]表示数列的偶数项。然后,遍历数列,对于每个位置i,计算an1[10]、an2[10]的值,最后二者交叉输出。
程序:
#include<stdio.h>
int main()
{
int an1[10]={1,1};
int an2[10]={2,3};
int n;
for(n=2;n<=9;n++)
{
an1[n]=an1[n-1]+an1[n-2];
an2[n]=an2[n-1]+an2[n-2];
}
printf("数列前20项为:");
for(n=0;n<=9;n++)
{
printf("%d,%d,",an1[n],an2[n]);
}
return 0;
}2.采用成对的完全平方数 x 和 y(x >y >= 1),生成 N 组可以构成直角三角形的三元组,并用二维数组存储这样的三元组。提示: 如果三角形三边长分别是a,b,c(a < c,b<c),令a=x-y,c=x+y,则b= 2(xy)½。在满要求的情况下,x和y的值可以任意设置
分析:可以先定义一个用于存储三元组的二维数组`triples`,然后通过一个循环来生成直角三角形的三元组。在循环中,程序首先计算两个完全平方数`x`和`y`,然后计算三角形的边长`a`、`b`和`c`。最后,将计算得到的三元组存储在`triples`数组中,并输出到控制台。
程序步骤:①定义存储三元组的二维数组`triples`
#define N 10 // 你可以根据需要修改N的值
int triples[N][3];
②通过一个循环来生成直角三角形的三元组
for (int i = 0; i < N; i++)
{
// 生成成对的完全平方数x和y
int x = (i+2)*(i+2); // 可以根据需要调整起始值
int y = 1;
// 计算三角形的边长
int a = x - y;
int c = x + y;
int b = 2 * sqrt(x * y);
③将计算得到的三元组存储在`triples`数组中,并输出
triples[i][0] = a;
triples[i][1] = b;
triples[i][2] = c;
printf("(%d, %d, %d)\n", triples[i][0], triples[i][1], triples[i][2]);
注意:该程序依赖于`<math.h>`库中的`sqrt()`函数,因此在编译时需要添加#include<math.h>以链接数学库。
程序:
#include <stdio.h>
#include <math.h>
#define N 10 // 你可以根据需要修改N的值
int main()
{
int triples[N][3]; // 存储三元组的二维数组
printf("生成的直角三角形三元组:\n");
for (int i = 0; i < N; i++)
{
// 生成成对的完全平方数x和y
int x = (i+2)*(i+2); // 可以根据需要调整起始值
int y = 1;
// 计算三角形的边长
int a = x - y;
int c = x + y;
int b = 2 * sqrt(x * y);
// 存储三元组
triples[i][0] = a;
triples[i][1] = b;
triples[i][2] = c;
printf("(%d, %d, %d)\n", triples[i][0], triples[i][1], triples[i][2]);
}
return 0;
}3.C语言对一维数据(假设有N个)进行排序,试分析最多需要对换元素的次数,何时会出现这种情况?
以下是对一维数据进行排序的方法和分析:
冒泡排序
冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换的元素,也就是说该数列已经排序完成。
冒泡排序的最坏时间复杂度为O(N^2),最好时间复杂度为O(N),平均时间复杂度为O(N^2)。
最多需要对换元素的次数为N*(N-1)/2,当原始数据是倒序排列时,会出现这种情况。
快速排序
快速排序是一种基于分治思想的排序算法,它的基本思想是通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,然后再按此方法对这两部分记录分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序的最坏时间复杂度为O(N^2),最好时间复杂度为O(NlogN),平均时间复杂度为O(NlogN)。
最多需要对换元素的次数为N*(N-1)/2,当原始数据是倒序排列时,会出现这种情况。
程序:
#include <stdio.h>
#include<stdlib.h>
#include<time.h>
#define N 6
void bubble_sort(int arr[], int n)
{
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main()
{
int m;
int arr[N];
printf("随机产生N个1~100的随机数:");
srand(time(NULL));
for(m=0;m<N;m++)
{
arr[m]=rand()%100+1;
printf("%d ",arr[m]);
}
printf("\n");
int n = sizeof(arr) / sizeof(arr[0]);
bubble_sort(arr, n);
printf("Sorted array: \n");
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}输出:注意随机数随机产生,每次输出结果不同。
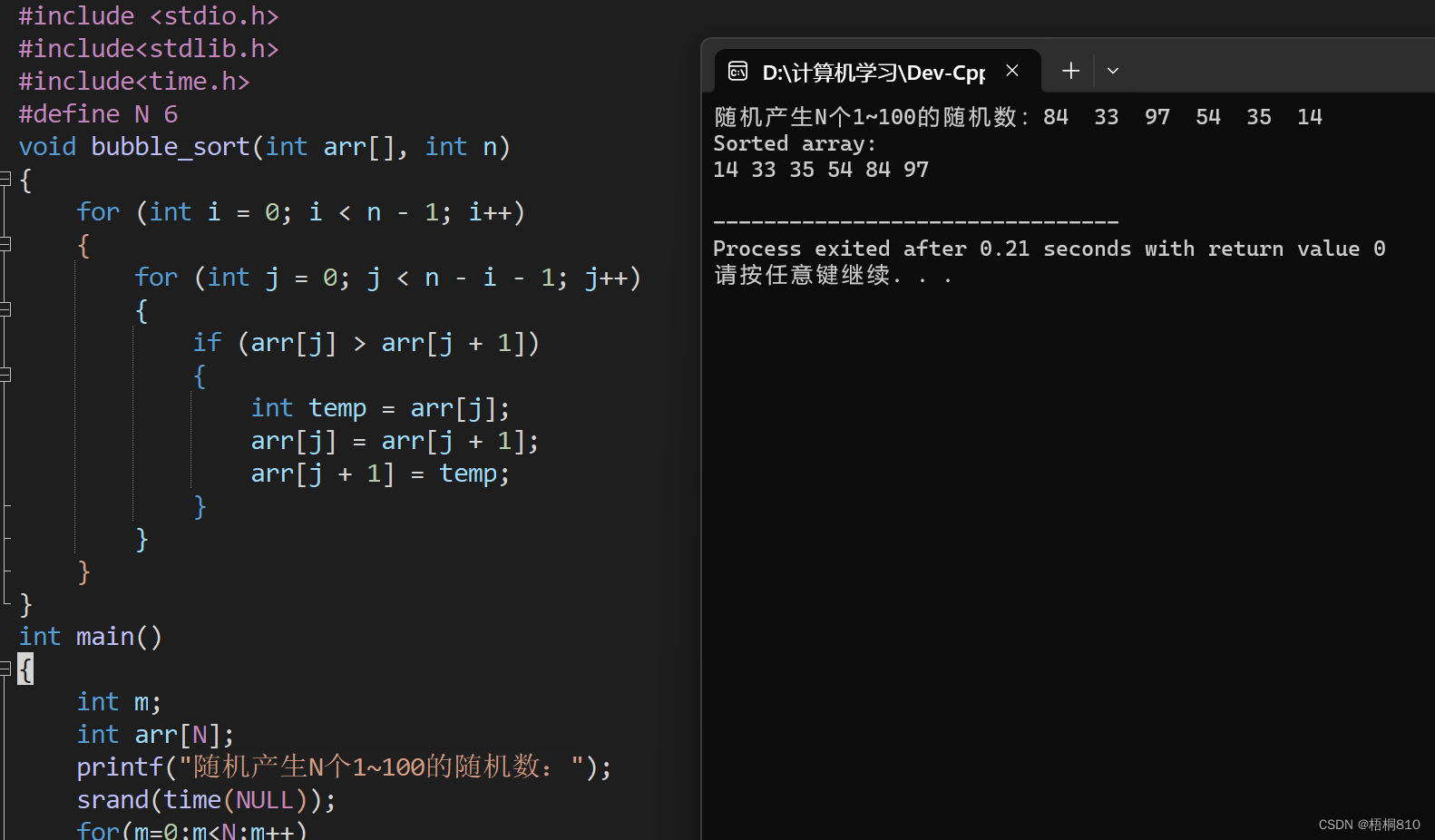
























 2232
2232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










