C语言数组【杨辉三角】【数列】

目录

杨辉三角

数列

第一种分析：实际上aₓ=Sₓ₋₁,可以通过循环计算Sₓ的值然后赋值给aₓ+₁,但注意此时Sₓ从第一项开始，数组a[21]有21项，最后只取前20项输出

第二种思路：先通过数学分析得出从第三项开始有aₓ=2aₓ₋₁,然后按这个思路写出程序

---

杨辉三角

分析：利用杨辉三角形的特性，从第i行生成第i+1行。设第i行数据保存在数组a中，第i+1行数据保存在数组b中。
输出时需要考虑居中问题。各行数据中每个数占8位，同时假设把第0行的1输出在屏幕的第30列处；那么第i行应从30-i*(8/2)处开始显示。

以输出八行为例
程序：

#include <stdio.h>
# define W 8/*定义每个数所占位置的宽度*/
int main ()
{
 	int a[8], b[8],i,j;
 	for (i=0;i<8;i++)/*生成八行数*/
	 {
	    for (j=1;j<8;j++)
	    	a[j]=b[j-1] + b[j];/*生成第i行*/
	    a[i]=1;
	    for(j=0;j<=i;j++)
	        b[j]=a[j];
        for(j=0;j<=36-i*(W/2);j++)
            printf("%c",' ');/*输出第i行前的空格,使形式整齐美观*/
        for(j=0;j<=i;j++)
	        printf("%8d",a[j]);/*输出第i行*/
        printf("\n");/*每行输出结束进行换行*/
	 }
	 return 0;
}

输出：

上面的杨辉三角问题也可采用下述方法实现：同样设第i行数据保存在数组a中，第i+1行数据保存在数组b中。程序运行时，数组a和b的角色可以对换，即在当前行数据a基础上生成下一行数据b；在下一次循环中，在b的基础上生成a，依次类推。此时程序如下：
程序：

#include <stdio.h>
#define N 8
int main ()
{
	int i=0, j=0, flag=0;
	int a[N] = {1};
	int b[N] = {1};
	do{
		if(!flag)
		{
			for (j=0;j<2*N-i;j++)
				printf("  ");
			j= 0;
			printf("%2d  ",b[j]);
			for(j=1;j<=i;j++)
			{
				b[j]=a[j]+a[j-1];
				printf("%2d  ",b[j]);
			}
			flag=1;
			printf("\n");							
		}
		else
		{
			for(j=0;j<2*N-i;j++)
			    printf("  ");
		    j =0;
			printf("%2d  ",a[j]);
			for(j=1;j<=i;j++)
            {
                a[j]=b[j]+b[j-1];
                printf("%2d  ",a[j]);
            } 
            flag=0;
			printf("\n");
		}	
		i = i + 1;
	}while (i<N);
	return 0;				
}

输出：

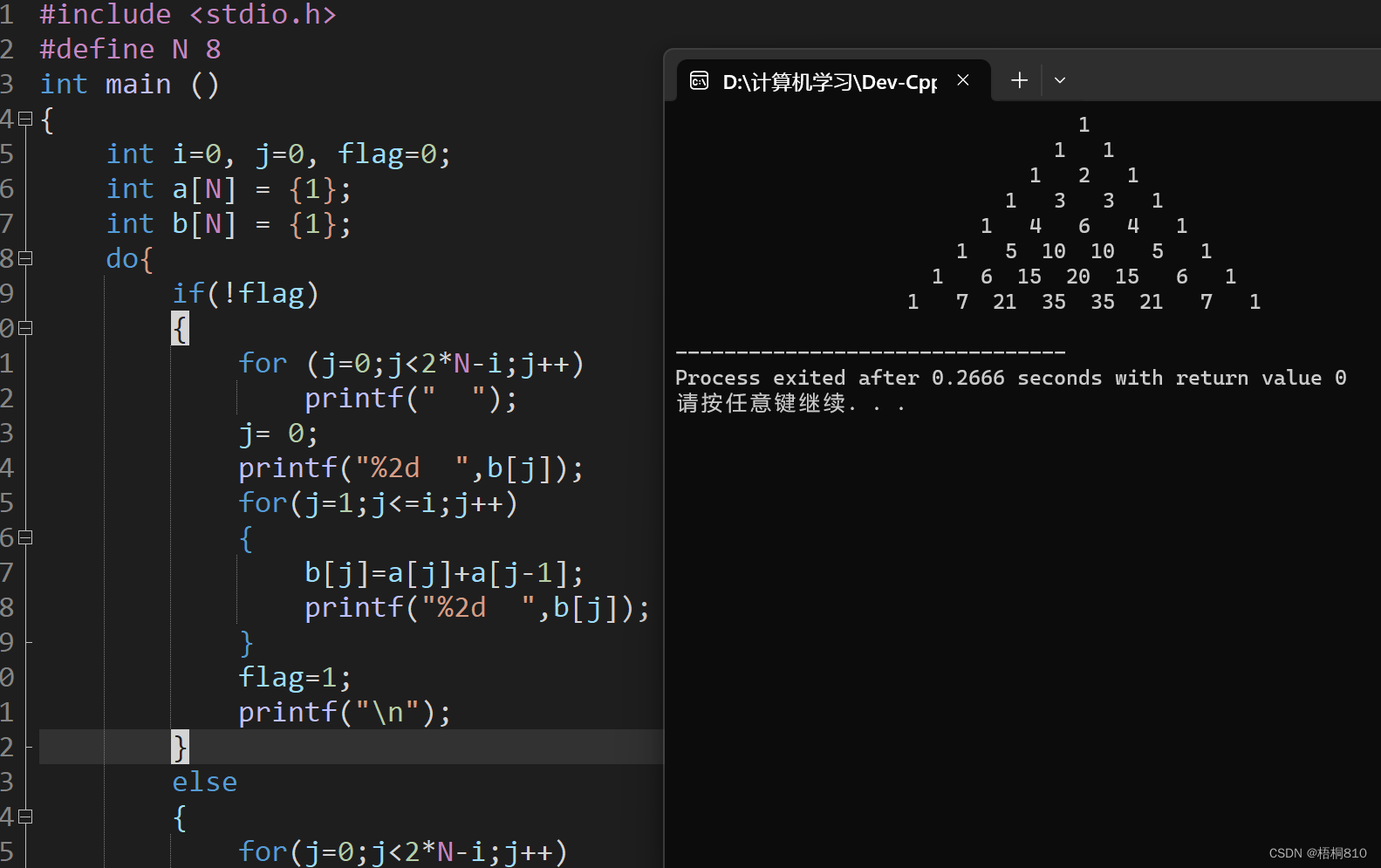
在printf每次输出数时，可以用printf("%4d")代替printf("%2d   ") 效果一样

数列

题目：已知数列a₁=1;x>1时,aₓ=a₁+a₂+aₓ₋₁,将该数列的前20项置入一个一维数组中(我没找到n的下角标所以这里用x代替n)。

第一种思路：实际上aₓ=Sₓ₋₁,可以通过循环计算Sₓ的值然后赋值给aₓ+₁,但注意此时Sₓ从第一项开始，数组a[21]有21项，最后只取前20项输出

程序：

#include<stdio.h>
#define N 21
int a[N];
int main()
{
    int sum=0;
    a[0] = 1;
    for(int j =0;j<20;j++)
	{
        sum = sum +a[j];
		a[j+1] = sum;
		printf("%d  ",a[j]);
    }
    return 0;
}

下面这个方法与上面类似，略有改动

#include<stdio.h>
#define N 20
int a[N];
int main()
{
    int sum=0;
    a[0] = 1;
    printf("%d  ",a[0]);
    for(int j =1;j<20;j++)
	{
        sum = sum +a[j-1];
		a[j] = sum;
		printf("%d  ",a[j]);
    }
    return 0;
}

第二种思路：先通过数学分析得出从第三项开始有aₓ=2aₓ₋₁,然后按这个思路写出程序

程序：

#include<stdio.h>
#define N 20
int a[N];
int main()
{
    int sum=0;
    a[0] = 1;
    a[1]=1;
    printf("%d  ",a[0]);
    printf("%d  ",a[1]);
    for(int j =1;j+1<20;j++)
	{
        sum = 2*a[j];
		a[j+1] = sum;
		printf("%d  ",a[j+1]);
    }
    return 0;
}

输出：

感谢各位大佬的阅读，有什么问题欢迎各位大佬指出，期待和大家共同进步。