审题:
本题要求我们求出最后剩下的孩子的编号
思路:
方法一:逆推法
我们首先顺着思考,在n个孩子的情况下,进行第一轮删除后,只剩下n-1个孩子,然后我们对删除的孩子的下一个孩子重新编号为0进行下一轮删除。而第二轮删除就可以看成是在n-1个孩子的情况下进行删除,也就是上一个环的子问题。
分析:
数量为n时,我们删除第一轮的数据编号为k=(m-1)%n,而我们将(k+1)%n当成数量为n-1时的新的0编号。
n 初始编号方式
n-1 编号方式2
n-2编号方式3
......
1 编号方式n
我们可以实现从第n个编号方式转换成第n-1个编号方式,从而将后面的编号转换回初始编号
综上,我们只要知道n==1的时候的最后删除的孩子的编号,以及从n-1的编号方式求出n的编号方式的式子,就可以解决该题
最后一个删除的孩子的编号由n和m共同决定
但是n=1的时候,无论m为多少,结果都是n==1下编号为0的孩子最后一个删除
(1)可得:f(1,m) = 0
接下来我们进行编号转换式子的推导:
设:
x为n-1编号方式的最后一个删除的节点的编号
y为n编号方式的最后一个删除节点的编号
而y等于原编号方式的第一轮删除的点的下一个点加上x(因为原编号方式的第一轮删除的点的下一个点就是下一次编号方式的0编号点,而我们在这里用k+1就相当于把新的0编号点转换成原编号方式的0编号点,我们在按原编号的0编号点加上x就得到y)
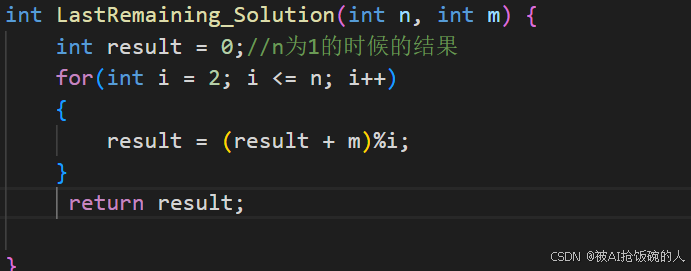
经过推导我们就可以得到编号方式转换的式子:result = (result + m)%i
解题:








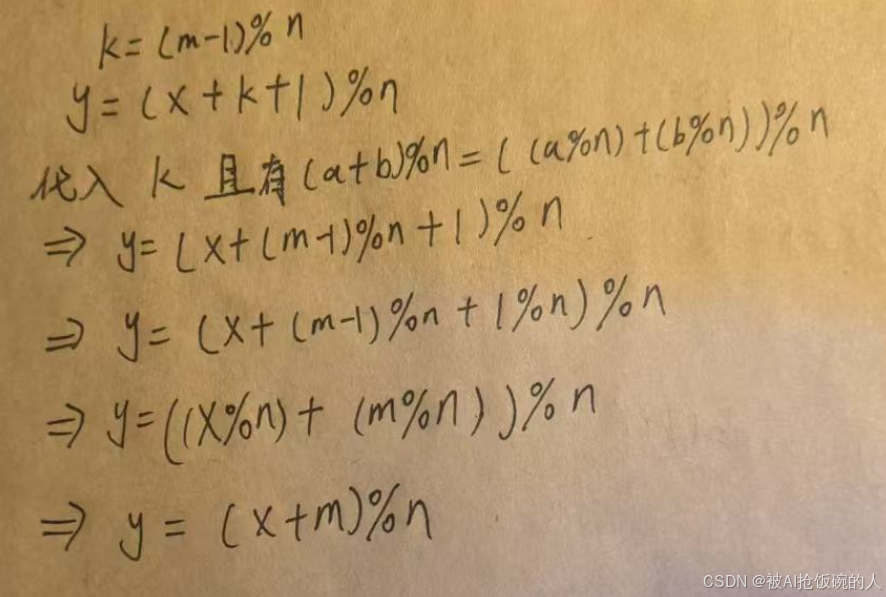
















 12万+
12万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








