【数据结构】五分钟自测主干知识（九）_visite结点有什么用-优快云博客

本文链接：https://blog.youkuaiyun.com/2301_79853895/article/details/136691346

上一节，我们讲述了“树”，而今天我们将来讲述二叉树——另一种重要的树形结构。

顾名思义，二叉树中每个结点的度都不超过2。二叉树具有存储表示简单，实现算法容易的特点，而且一般的树或森林也能方便地转换为相应的二叉树。因此，二叉树是树形结构中重点讨论的对象。

5.2二叉树

二叉树（Binary Tree）是 $n\left ( n\geq 0 \right )$ 个结点的有限集，它或者是空集（n=0），称为空二叉树；或者是由一个根结点及两棵互不相交的、分别称为左子树和右子树的二叉树组成。

显然，这也是一种递归定义，即在二叉树定义中用到了二叉树的概念。

我们不能把二叉树看成是树的特例，尽管他们具有树形结构的共同特征：层次性和分支性。

二叉树可以是空二叉树。非空二叉树的根结点必定有2棵子树（无论根结点的度是0,1还是2）——左子树和右子树，它们也是二叉树，可以为空，且左右次序不能颠倒。因此，二叉树可以有五种基本形态。

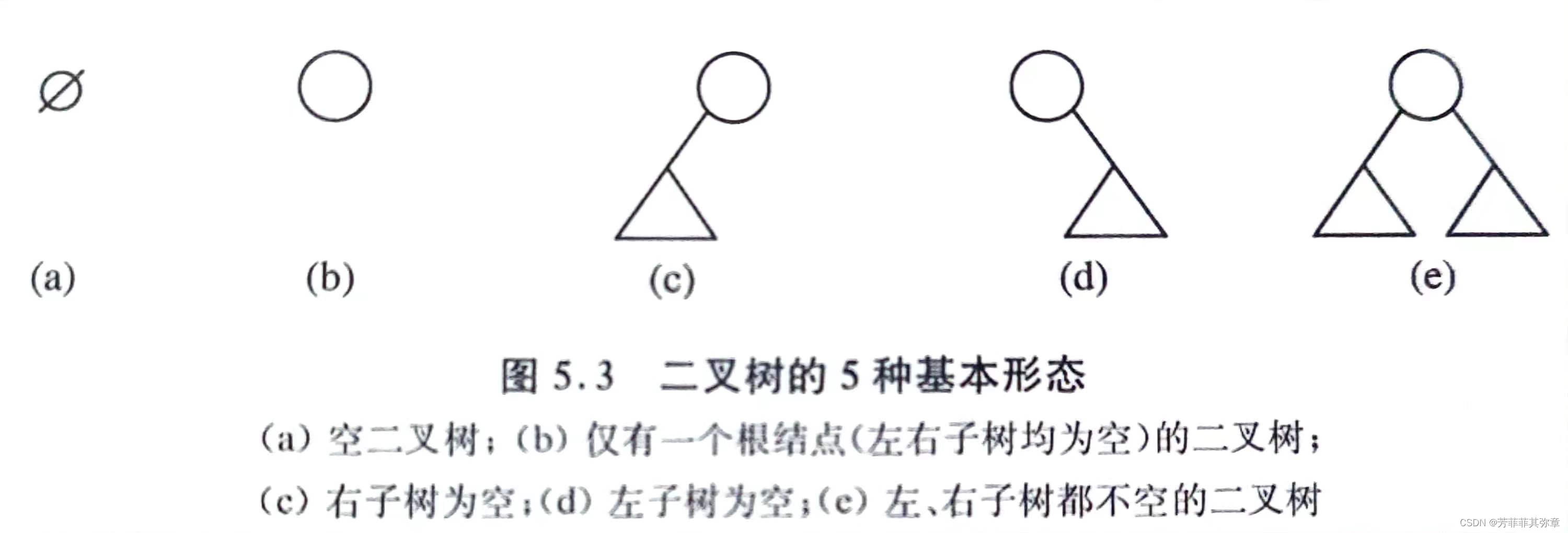
下面给出二叉树的抽象数据类型的定义：

ADT BinaryTree{
数据对象 D:D 是同类型数据元素的集合。
数据关系 R:若 $D=\varnothing$ ,则称 BinaryTree 为空二叉树;
否则R是满足下列条件的二元关系:
(1)在D中存在唯一的称为根的元素 root,它在R下无直接前驱;
(2)若 $D-\left \{ root \right \}=\varnothing$ ,则 $R=\varnothing$ ;否则存在 $D-\left \{ root \right \}=\left \{ D_1,D_r \right \}$ ,且 $D_1\bigcap D_r=\varnothing$ ;
(3)若 $D_1\neq \varnothing$ ,则 $D_1$ 中存在唯一的元素 $x_1$ , $\left \langle root,x_1 \right \rangle \in R$ ,且存在 $D_1$ 上的关系 $R_1\subset R$ ;若 $D_r \neq \varnothing$ ,则 $D_r$ 中存在唯一的元素 $x_r$ , $\left \langle root,x_r \right \rangle \in R$ ,且存在 $D_r$ 上的关系 $R_r\subset R$ ; $R=\left \{ \left \langle root,x_1 \right \rangle,\left \langle root,x_r \right \rangle ,R_1,R_r\right \}$ ;
(4)(D,R)是一棵符合本定义的二叉树,称为根的左子树;(D,R)是一棵符合本定义的二叉树,称为根的右子树。

基本操作 P：

InitBifree(&T)
操作结果:构造空二叉树 T。

DestroyBiTree(&T)
初始条件:二叉树 T 已经存在。
操作结果:销毁 T。

CreateBiTree(&T)
操作结果:按某一规则,创建二叉树 T。

TreeEmpty(T)
初始条件:二叉树T已经存在。
操作结果:如果T是空二叉树,则返回 TRUE;否则返回 FALSE。

ClearTree(&T)
初始条件:二叉树已经存在。
操作结果;删去T中的全部结点,使T成为空二叉树。

TreeDepth(T)
初始条件:二叉树T已经存在。
操作结果:返回T的深度。如果T为空二叉树,则返回 0。

Root(T)
初始条件:二叉树T已经存在。
操作结果:返回T的根。

Parent(T, x)
初始条件:二叉树T已经存在,x是T中的一个结点。
操作结果:返回x的双亲结点。如果x是树根,则返回“空”。

LeftChild(T, x)
初始条件:二叉树T已经存在,x是T中的一个结点。
操作结果:返回x的左孩子。如果x无左孩子,则返回“空”。

RightChild(T,x)
初始条件:二叉树T已经存在,x是T中的一个结点。
操作结果:返回x的右孩子。如果x无右孩子,则返回“空”。

LeftSibling(T,x)
初始条件:二叉树T已经存在,x是T中的一个结点。
操作结果:返回×的左兄弟。如果x无左兄弟,则返回“空”。

RightSibling(T,x)
初始条件:二叉树 T已经存在,x是T中的一个结点。
操作结果:返回x的右兄弟。如果x无右兄弟,则返回“空”。

InsertChild(&T,x,LR,c)
初始条件:二叉树T已经存在,x是T中的一个结点,LR为 0 或 1,c是另一棵与T不相交的
非空二叉树,且c 的右子树为空。
操作结果:根据 LR为0 或 1,将c插到T中,使之成为结点x的左子树或右子树。x原有的
左子树或右子树则成为 c 的右子树。

DeleteChild(&T,x,LR)
初始条件:二叉树T已经存在,x是 T 中的一个结点,LR为 0 或 1。
操作结果:根据 LR为0或1,删除结点x的左子树或右子树。

TraverseTree(T,visite())
初始条件:二叉树T已经存在,visite()是对结点进行访问的应用函数。
操作结果:按某种规则对T中的每个结点调用 visite()一次且仅一次。

}end ADT BinaryTree

二叉树的性质，其中一部分被包含在“树”里面（其中k=2）

附链接：【数据结构】五分钟自测主干知识（八）

http://t.csdnimg.cn/tfYU3http://t.csdnimg.cn/tfYU3

满二叉树：

在一棵二叉树中，如果所有分支结点的度都等于2，且·所有叶子结点都在同一层上，则这棵二叉树称为满二叉树。

完全二叉树：

对一棵深度为h，具有n个结点的二叉树从第一层开始自上而下，自左至右地连续编号 $1,2,\dots ,n$ ,如果编号为 $i(1\leq i\leq n)$ 的结点与深度为h的满二叉树中编号为i的结点位置完全相同，则这棵二叉树称为完全二叉树。

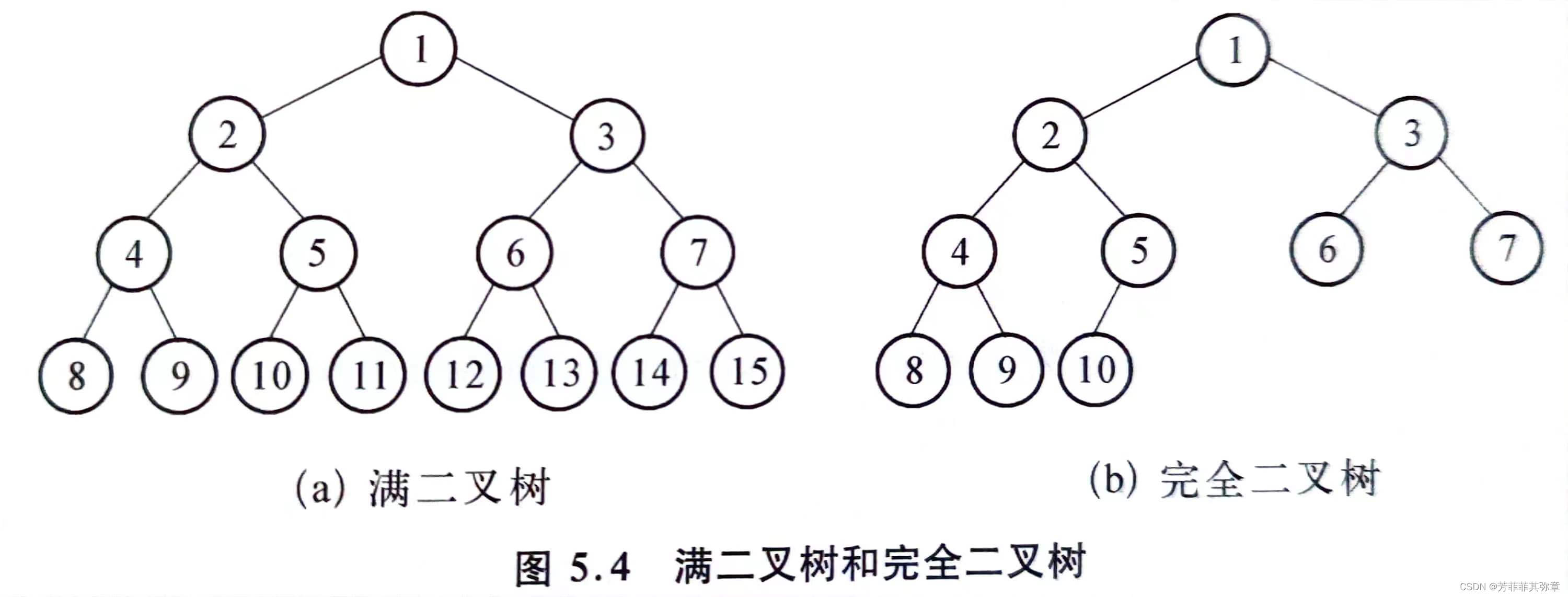
可见，满二叉树是完全二叉树的一个特例。在深度为h的完全二叉树中，前h-1层是满二叉树。

二叉树的宽度定义为：若某一层的结点数不少于其他层次的结点数，那么该结点数即为二叉树的宽度。很显然，满二叉树也是深度相同的二叉树中宽度最大的二叉树。

特殊性质：
☞具有n个结点的完全二叉树，其深度为 $\left \lfloor \log_2n \right \rfloor+1$ 。

☞对于具有n个结点的完全二叉树从树根开始自上而下、自左至右地连续编号 $1,2,\dots,n$ ,对于任意的编号为 $i(1\leq i \leq n)$ 的结点 $x$ ，有：

（1）若i=1，则x是根结点，无双亲；否则x的双亲的编号为 $\left \lfloor i/2 \right \rfloor$ 。

（2）若2i>n，则x是叶子结点，无左孩子；否则x的左孩子的编号为2i。

（3）若2i+1>n，则x无右孩子；否则x的右孩子的编号为2i+1。

（4）若i是奇数且不为1，则x的左兄弟的编号为i-1；否则x无左兄弟。

（5）若i是偶数且小于n，则x的右兄弟的编号为i+1；否则x无右兄弟。

二叉树的存储结构

1.顺序存储结构

用一个一维数组存储，不推荐（因为会留下很多空集）

下面给出二叉树顺序存储结构的类型定义

#define MAXSIZE 100
typedef int TElemType;
typedef struct {
	TElemType Nodes[MAXSIZE + 1];
	int n;
}SqBiTree;

2.链式存储结构

每个结点除了数据域外，还需设置两个指针域：左指针lchild和右指针rchild，分别用来指向该结点的左孩子和右孩子。这种链式存储结构称为二叉链表。

typedef struct BiTNode {
	TElemType data;
	struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;

在二叉链表上，通过左指针和右指针可以直接找到一个结点的孩子，但不能直接找到它的双亲。

为了便于找到双亲，可以在二叉链表的结点结构中再增加一个指向双亲的指针域parent，这种链式存储结构称为三叉链表。

为了让树这一章分解梳理，我暂且先写到这，下一节，我们可以复习二叉树的遍历及应用~

基础概念较多，好好吸收

下一讲，附链接：【数据结构】五分钟自测主干知识（十）

http://t.csdnimg.cn/3ecKRhttp://t.csdnimg.cn/3ecKRIt's so nice to meet you.See you soon~