【数据结构】五分钟自测主干知识（八）-优快云博客

本文链接：https://blog.youkuaiyun.com/2301_79853895/article/details/136676719

前面我们学习的线性表是一种线性结构。其逻辑特征是元素之间存在“一对一”的联系，即除了首元素之外，每个元素有且仅有一个直接前驱；除了表尾元素外，每个元素有且仅有一个后继。

而树形结构是一种重要的非线性结构。

非线性结构的逻辑特征是每个元素可能存在多个直接前驱和多个直接后继。在树形结构中，每个元素至多有一个直接前驱，但可能有多个直接后继，有“一对多”的关系。

树形结构中，以树和二叉树最为常用。

5.1树

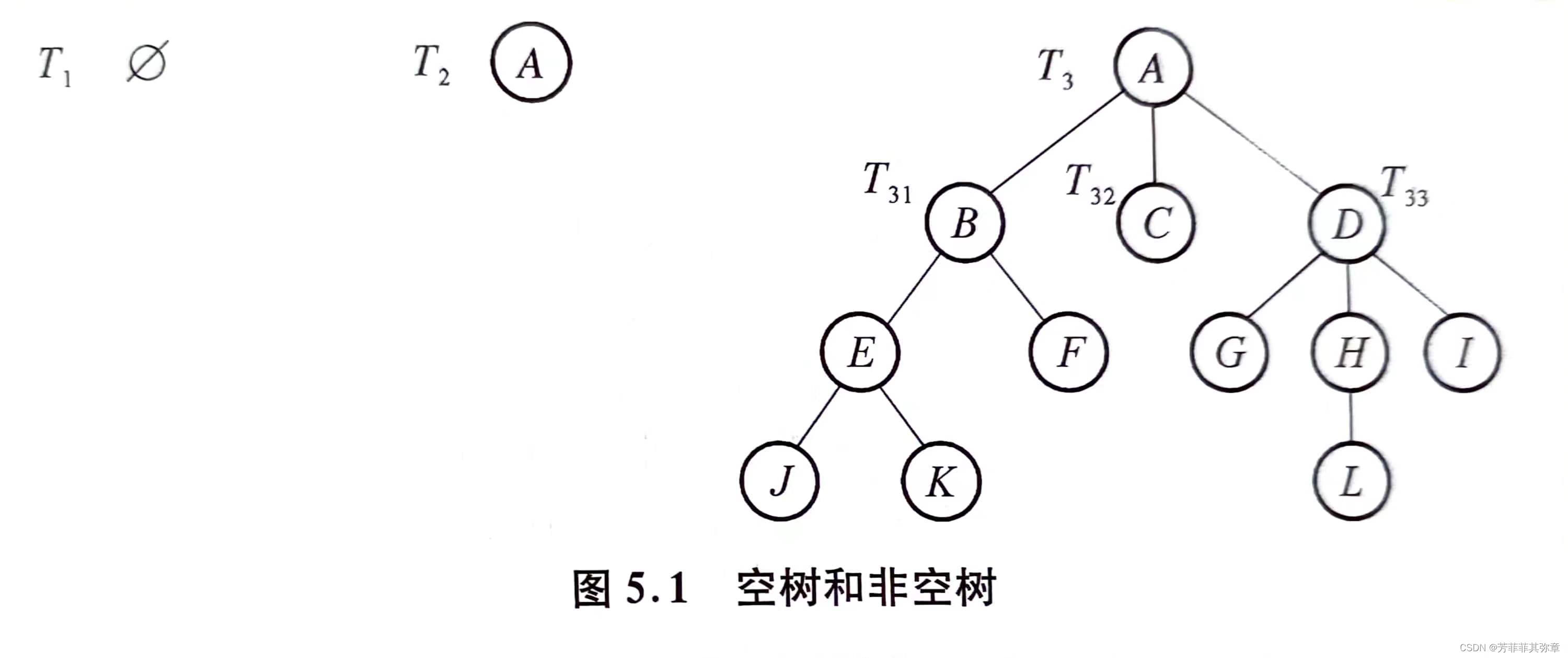
树（Tree）是n（n≥0）个结点的有限集。当n=0时，称为空树；在任意一棵非空树中：

1.有且仅有一个特定的称为根（Root）的结点；

2.当n>1时，除了根结点之外其余结点可分为m(m>0)个互不相交的子集，其中每个子集又是一棵树，称为根的子树（Subtree）。

树的定义是一种递归定义

递归是树的固有特性，一棵非空树由一个根结点及若干个子树构成，而子树又可以由其根结点和若干棵更小的子树构成。

树具有层次性和分支性

下面给出树的抽象数据类型的定义：
ADT Tree{
数据对象 D:D 是同类型数据元素的集合。
数据关系 R:若D=Ø,则称为空树；
        否则R是满足下列条件的二元关系：
        (1) D中存在唯一的称为根的元素 root,它在R下无直接前驱。
        (2)若 $D-\left \{ root \right \}=\varnothing$ ,则 $R=\varnothing$ ;否则存在 $D-\left \{ root \right \}$ 的一个划分 $D_1,D_2,\dots,D_m(m>0)$ ,对任意的 $j\neq k(1\leq j,k\leq m)$ ,有 $D_j\bigcap D_k=\varnothing$ ,且对任意的 $i(1\leq i\leq m)$ ,存在唯一的数据元素 $x_i\in D_i$ ,有 $\left \langle root,x_i \right \rangle \in R$ ;
        (3)对应于 $D-\left \{ root \right \}$ 的划分, $R-\{{\left \langle root,x_1 \right \rangle},\dots,\left \langle root,x_m \right \rangle\}$ 有唯一的一个划分 $R_1,\dots,R_m(m>0)$ ,对任意的 $j\neq k(1\leq j,k\leq m)$ ,有 $R_j \bigcap R_k=\varnothing$ ,且对任意的 $i(1\leq i\leq m)$ , $R_i$ 是 $D_i$ 上的二元关系。 $(D_i,R_i)$ 是一棵符合本定义的树,称为根 root 的子树。
基本操作 P：
InitTree(&T)
操作结果:构造空树 T。

DestroyTree(&T)
初始条件:树T已经存在。
操作结果:销毁 T。

CreateTree(&T)
操作结果:按某一建树规则,创建树 T。

TreeEmpty(T)
初始条件:树T已经存在。
操作结果:如果T是空树,则返回 TRUE;否则返回FALSE。

ClearTree(&T)
初始条件:树T已经存在。
操作结果:删除T中全部结点,将T变为空树。

TreeDepth(T)
操作结果:返回T的深度。如果T为空树,则返回 0。
初始条件:树T已经存在。

Root(T)
初始条件:树T已经存在。
操作结果:返回T的根。

Parent(T, x)
初始条件:树T已经存在,x是T中的一个结点。
操作结果:返回×的双亲结点。如果x是树根,则返回“空”。

FirstChild(T,x)
初始条件:树T已经存在,x是T中的一个结点。
操作结果:返回×的第一个孩子。如果x是树叶,则返回“空”。树的孩子逻辑上没有先后之分,这里第一个是指物理存储里第一个。

NextSibling(T,x)
初始条件:树T已经存在,x是T中的一个结点。
操作结果:返回×的下一个兄弟。如果x是双亲的最后一个孩子,则返回“空”。

InsertChild(&T,x,i,p)
初始条件:树T已经存在,x是T中的一个结点,1 ≤ i ≤ (x的度+1),p 是另一棵非空树。
操作结果:将p插到T中,使之成为结点x的第i棵子树。

DeleteChild(&T,x, i)
初始条件:树T已经存在,x是T中的一个结点,1 ≤ i ≤ x的度。
操作结果:删除结点x的第i棵子树。

TraverseTree(T,visite())
初始条件:树T已经存在,visite()是对树结点进行访问的某应用函数。
操作结果:按某种规则对T中每个结点调用 visite()一次且仅一次。

}end ADT Tree

有关树的术语

（1）结点（Node）：包含一个数据元素以及指向其子树的分支。

（2）结点的度（Node Degree）：结点拥有子树的个数称为该结点的度。

（3）树的度（Tree Degree）：非空树中各结点的度的最大值称为该树的度。

（4）分支结点（Offshoot Node）：树中度不等于0的结点称为分支结点，也称为非终端结点。

（5）叶子结点（Leaf Node）：树中度等于0的结点称为叶子结点，也称为终端结点。

（6）孩子（Child）：结点子树的根（即结点的直接后继）称为该结点的孩子。

（7）双亲（Parent）：结点的直接前驱称为该结点的双亲。显然，根结点没有双亲。

（8）兄弟（Sibling）：同一个双亲的结点之间互为兄弟。

（9）祖先（Ancestor）：从树根到某结点所经分支上的所有结点都是该结点的祖先。

（10）子孙（Descendant）：某结点所有子树上的所有结点都是该结点的子孙。

（11）结点的层次（Level）：在非空树中，根结点的层次定为1，其余结点的层次是其双亲结点的层次加1。

（12）树的深度（Tree Depth）：空树的深度为0；在非空树中，所有结点层次的最大值称为该树的深度或高度（Height）。

（13）有序树和无序树（Ordered Tree and Unordered Tree）：如果一棵树中结点的各个子树从左至右是有次序的，即交换了子树的相对位置就构成了不同的树，则称该树为有序树。反之为无序树。

（14）森林（Forest）：由m（m≥0）棵互不相交的树组成的集合。在数据结构中，树和森林是很相近的概念：删除一棵树的根结点，根的各个子树就形成了一个森林；反之，以一个森林的m棵树为子树，再加一个根结点，就形成了一棵树。

树的几个性质

性质1

设树有 $n(n\geq 1)$ 个结点，每个结点的度为 $d_i(i=1,2,\dots,n)$ ,则有

$n=\sum_{i=1}^{n}d_i+1$

证明：除了树根以外，每个结点有且仅有一个直接前驱。

所以树中分支数 $B=n-1$ 。又，树的分支数 $B$ 等于树中每个结点的度之和，带入即可证。

性质2

度为k的树（k叉树），其第 $i(i\geq 1)$ 层至多有 $k^{i-1}$ 个结点。

证明：使用数学归纳法。

树的第一层只有1个结点（树根结点）故 $i=1$ 时， $k^{1-1}=k^0=1$ ,命题成立。

设树的第 $i-1$ 层（i>1）命题成立，即第 $i-1$ 层有至多 $k^{i-2}$ 个结点。由于第 $i-1$ 层上，每个结点最多有k个孩子，所以第 $i$ 层的结点数至多为 $k^{i-2}\times k=k^{i-1}$ ,证毕！

性质3

深度为 $h(h\geq 1)$ 的 $k$ 叉树，至多有 $\frac{k^h-1}{k-1}$ 个结点。

证明：深度为h的k叉树，其最大结点数为各层最大结点数之和，根据性质2： $\sum_{i=1}^{h}k^{i-1}=\frac{k^h-1}{k-1}$

性质4

具有 $n(n\geq 1)$ 个结点的 $k(k>1)$ 叉树，其最小深度为 $\left \lceil \log_k(n(k-1))+1\right \rceil$ （取整）

证明：

设具有n个结点的k叉树深度为h，若前h-1层的每层结点数都达到最大值 $k^{i-1}(1 \leq i\leq h-1)$ ,余下的结点都分布在第h层上，则该树的深度达到最小。根据性质3有

$\frac{k^{h-1}-1}{k-1}<n\leq \frac{k^h-1}{k-1}$

或

$k^{h-1}<n(k-1)+1\leq k^h$

取对数得

$h-1<\log_k[n(k-1)+1]\leq h$

即有

$\log_k[n(k-1)+1]\leq h<\log_k[n(k-1)+1]+1$

由于h是正整数，则有 $h=\left \lceil \log_k(n(k-1))+1\right \rceil$ 得证！

今天的基础概念颇多，我们下一讲进入另一个重要的树形结构——“二叉树”的理论复习

明天见！

附链接：【数据结构】五分钟自测主干知识（九）

http://t.csdnimg.cn/BIXhhhttp://t.csdnimg.cn/BIXhh