一文彻底搞懂二分算法的细节

最新推荐文章于 2025-02-21 23:44:37 发布

东洛的克莱斯韦克

最新推荐文章于 2025-02-21 23:44:37 发布

阅读量1k

点赞数 26

分类专栏：算法文章标签：算法二分算法力扣刷题

本文链接：https://blog.youkuaiyun.com/2301_79796701/article/details/143557344

版权

算法专栏收录该内容

13 篇文章

订阅专栏

朴素二分

当数组有序时，我们可以用二分索引一个值。left指针在数组左边，right指针在数组右边，mid是数组的中间值。

mid = left + (right - left) / 2 -------> mid永远都是中间值。

加入数据是升序，当mid索引到的数据大于或小于mid时，可以让left = mid + 1 或 right = mid -1 。每次索引都能排除当前剩余数据的一半，举个例子，如果有2亿数据量，一次索引就可以排除1亿数据量。这种算法的事件复杂度是 O( $logN$ ) ，相较于 O(N)，它可以指数级的降低时间复杂度。

来看一道题-------->704. 二分查找 - 力扣（LeetCode）

代码示例

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        while (left <= right) {
            int m = left + (right - left) / 2;
            if (nums[m] < target)  left = m + 1;
            else if (nums[m] > target) right = m - 1;
            else return m;
        }
        return -1;
    }
};

求中间值 mid 时，下述写法可以防止 mid 溢出，这时二分查找的细节之一。

left + (right - left) / 2

非朴素二分

非朴素二分是在朴素二分的思想上进行泛化，判断一道题是否需要二分算法不在是“数组是否有序” 这样的看法，而是 “数组有没有二段性” 。二段性是指可以用某个条件把数组区分成不同的两段。

来看一道题------->34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目描述的非递减顺序是指数据可以递增也可以不变。target 作为目标值，让我们找一段值为target的区间。

区间是一段数据，听上去好像不能用二分查找，因为二分查找只能找一个数据。我们可以用两次二分分别找到区间的左端点和区间的右端点即可。这种算法的时间复杂度依然是 O( $logN$ )。

用二分算法分别找到区间的左端点和区间的右端点听上去简单，其实细节非常多。下面我以这道题为例分析 “用二分算法分别找到区间的左端点 ”的细节

细节分析

示例：

nums = [5,7,7,8,8,10], target = 8

指针初始化：left = 0 , right = nums.size() - 1;

mid 在数组中有三种命中情况

1. 命中区间的左边：nums[mid] < target

2.命中区间的右边：nums[mid] > target

3.命中区间某个值：nums[mid] = target

把情况2 和 3 合并，数组一定不是降序，我们可以分析其中的二段性

1. nums[mid] < target：left ~ mid 这个区间一定是全都小于target。那么我们应该去 mid + 1 ~ right 这个区间里寻找区间的左端点，如下图示意

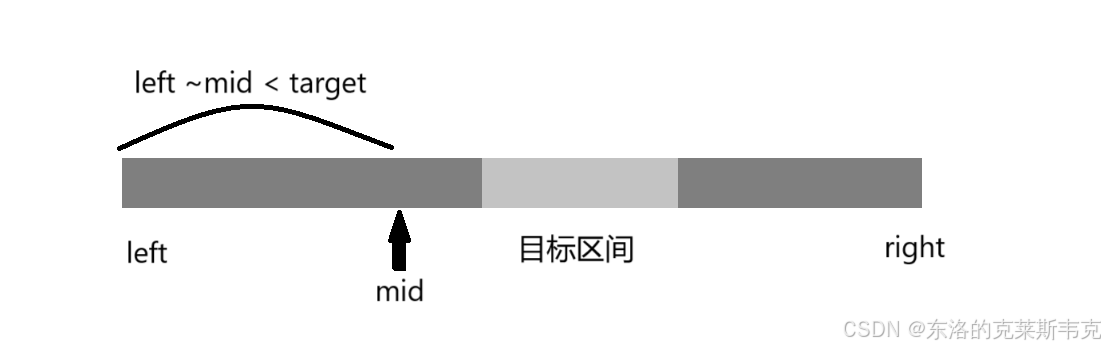
2.nums[mid] >= target：right ~ mid 区间全部大于大于或等于target ，那么我们应该去 mid ~ left 这个区间里寻找区间的左端点，为什么不是 mid - 1 ~ left呢？因为mid 可能刚好是区间的左端点，如下图示意。

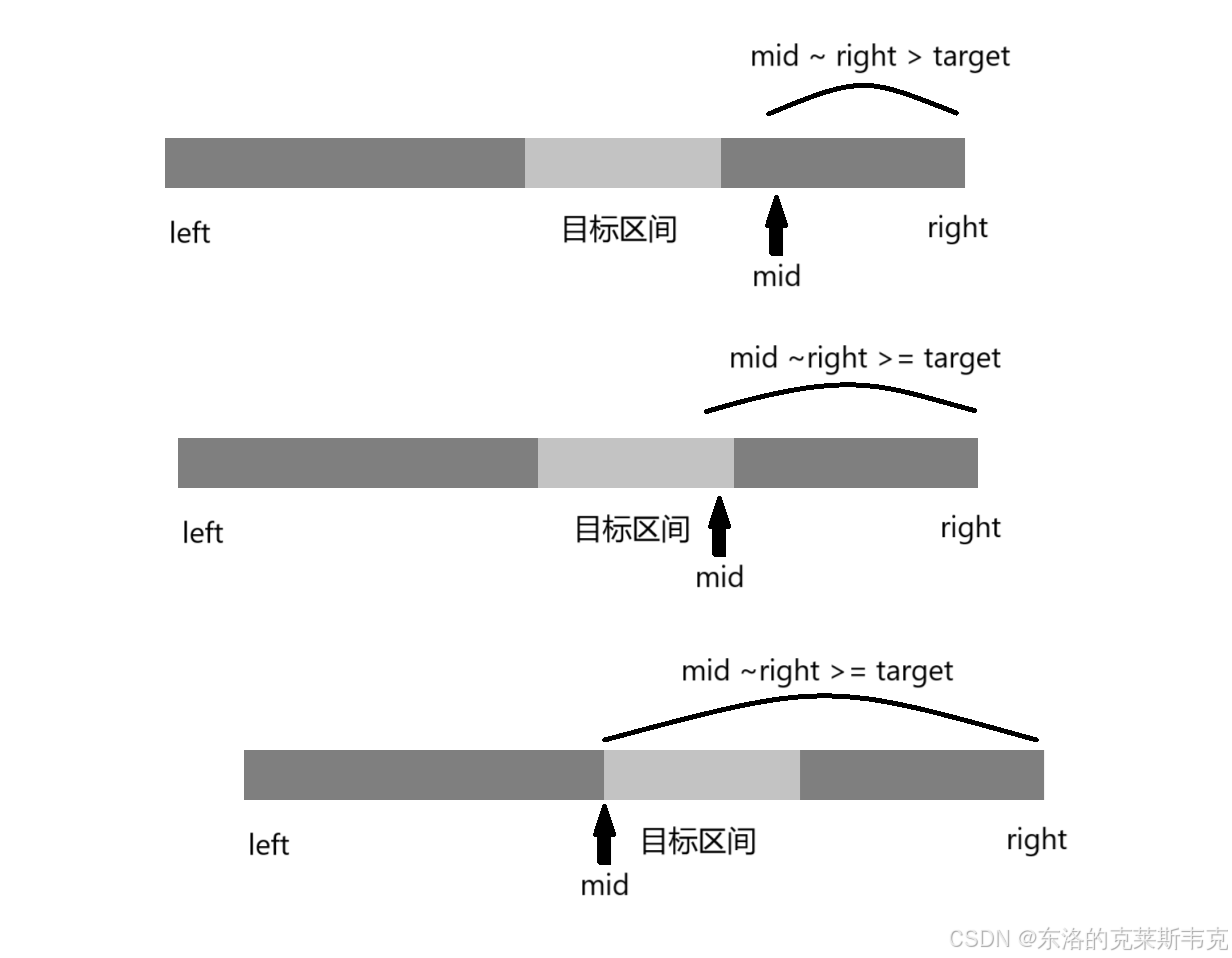
这里总结第一个细节

nums[mid] < target ：left = mid + 1；

nums[mid] >= target ：right = mid;

第二个细节求中点的值，有两种写法

left + (right - left) / 2

left + (right - left + 1) / 2

当数组长度为偶数时，有两个中间值（有两个mid），第一种写法mid会命中前一个中间值（靠近left），第二种写法mid会命中后一个中间值（靠近right）。我们在查找区间左端点时，应该用第一种写法，left + (right - left) / 2不会命中right，因为我们更新right下标时是right = mid，如果让mid命中right下标就会一直right = mid 循环下去。

第三个细节，就是出循环的判断条件，有两种写法

left < right

left <= right

我们选用第一种写法，因为left <= right 可能会死循环，left = right进入循环，nums[mid] >= target条件成立，更新下标right = mid，还会再次陷入循环。

查找区间右端点也类似，这里先给出代码示例

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        std::vector<int> ret;
        int len = nums.size();
        if (len == 0) return {-1, -1};
        int left = 0, right = len -1, m = 0;
        //查找区间左端点
        while (left < right) {
            m = left + (right - left) / 2;
            if (nums[m] < target) left = m + 1;
            else right = m;
        }
        if (nums[left] == target) ret.push_back(left);
        
        //查找区间右端点
        left = 0; right = len - 1;
        while (left < right) {
            m = left + (right - left + 1) / 2;
            if (nums[m] <= target) left = m;
            else right = m -1;
        }
        if (nums[left] == target) ret.push_back(left);
        else return {-1, -1};

        return ret;
    }
};

模板总结

查找区间左端点：

循环条件：left < right

下标更新：if (...) left = mid + 1 ; if (...) right = mid;

中点值mid：left + (right - left) / 2

查找区间左端点：

循环条件：left < right

下标更新：if (...) left = mid; if (...) right = mid - 1;

中点值mid：left + (right - left + 1) / 2

模板的思想总结：

当下标更新为if (...) left = mid + 1 ; if (...) right = mid; 时，说明左区间完全不符合条件，右区间有可能符合条件，所以mid + 1表示left想跳出完全不符合条件的区间， right = mid 说明right尽可能地不漏掉符合条件地数据然后缩小查找区间（left ~ right）。

查找区间右端点也是如此。

而中点值地选择要看下标是如何更新的。如果是left = mid + 1，mid应该靠左，所以选择left + (right - left) / 2，如果是 right = mid - 1，mid应该靠右，所以选择left + (right - left + 1) / 2。