专题---过拟合

1.定义

①在“蒲公英”书上：

模型在训练集上错误率很低，但在未知数据上错误率很高。

过度拟合，overfitting，在已知的数据上训练表现良好，而在未见过的测试数据上表现较差。

举个例子：我们来拟合一个函数来根据每个月份的气温预测未来的气温：

例子1.1

我们可以用肉眼看到左边的函数明显过拟合了，它能很好的表现已知的每个月的气温，但是在未知数据上的预测能力很差。

相反，右边的函数看起来很简单，虽然它在已知的数据上表现得不是很好，但是它能够在未来的数据上表现得很好。

于是：我们可以理解到精确解释一起过去发生的理论，极大概率都是一个错到离谱的理论。

②PAC学习理论

③广义

在生活中很常见，比如，我们很容易把一些物品误认为人脸；

平时过度的刷题结果在考场上做不出新题目。

这些都是因为我们大脑过拟合了。

2.原因

为什么会出现过拟合？

以例子1.1为例：是因为模型过分敏感地受到数据集中噪声的影响。在进行算法计算时，算法首先选择能贴合所有数据集地模型，自然在左边右边中选择左边的。

拉格朗日插值法：

给定n+1个点，有唯一一个n次多项式恰好经过它。

————>  "偏差为0， 完美无缺”

所以在我们给定12个数据气温，就有一个11次多项式能够经过这12个点。

那么就要求我们算法在选择模型时选择较简单的那个。

也就是奥卡姆剃刀：在所有解释中，最简单的那个往往是最正确的。（如无必要，勿增实体）

以下几类情况会出现过拟合？

1.训练数据过少，质量不高 样本数据不足以代表预定的分类规则

2.训练模型复杂度较高

3.模型训练时间过长，过度贴合噪声  对于神经网络模型：1.权值学习迭代次数太多(Overtraining)，BP算法使权值可能收敛过于复杂的决策面

4.样本噪音干扰过大  使得机器将学习了噪音，还认为是特征，从而扰乱了预设的分类规则

3.判定

训练集的errory不断降低，而测试集的误差不断升高。

4.解决

1.增加数据量 

通过数据增强或收集更多数据来提高模型的泛化能力。   

  

如图增加数据前与增加数据后。

2.简化模型   

减少模型的层数或参数数量。    

 如无必要，勿增实体   

举个例子：一道找规律的题目  1， 3， 5， 7 ， ___?

答案是9吗？如果出题人说不是，正确答案是114514？那我们的答案有错了吗？

我们之所以填9是因为我们是根据等差数列 f(x)=2x - 1得到的，而另一个答案是根据下面这个式子

那为什么我们从小到大的找规律题目的正确答案都是填9？显然第一个函数的系数更简单，我们自然选择第一个模型。这就是解决过拟合的简化模型

3.早停法

在训练过程中，当验证误差不再下降时停止训练。对模型进行迭代训练时，我们可以度量每次迭代的性能。当验证损失开始增加时，我们应该停止训练模型

4.正则化

线性回归模型的损失函数

1.L1正则化

2.L2正则化

1.为什么正则化可以减少过拟合？

我们知道过拟合是由于模型的复杂程度过高，训练样本过少引起的，而模型的复杂程度是由参数个数及参数大小范围所决定的，因此通过控制参数w可以减小过拟合。

2，为什么只对w限制，不对b进行限制？

b是偏移量，仅仅对函数上下平移，不改变其复杂程度。而解决过拟合说直白一点其实就是让函数变得更加平滑一点。

3.L1正则化与L2正则化的表现

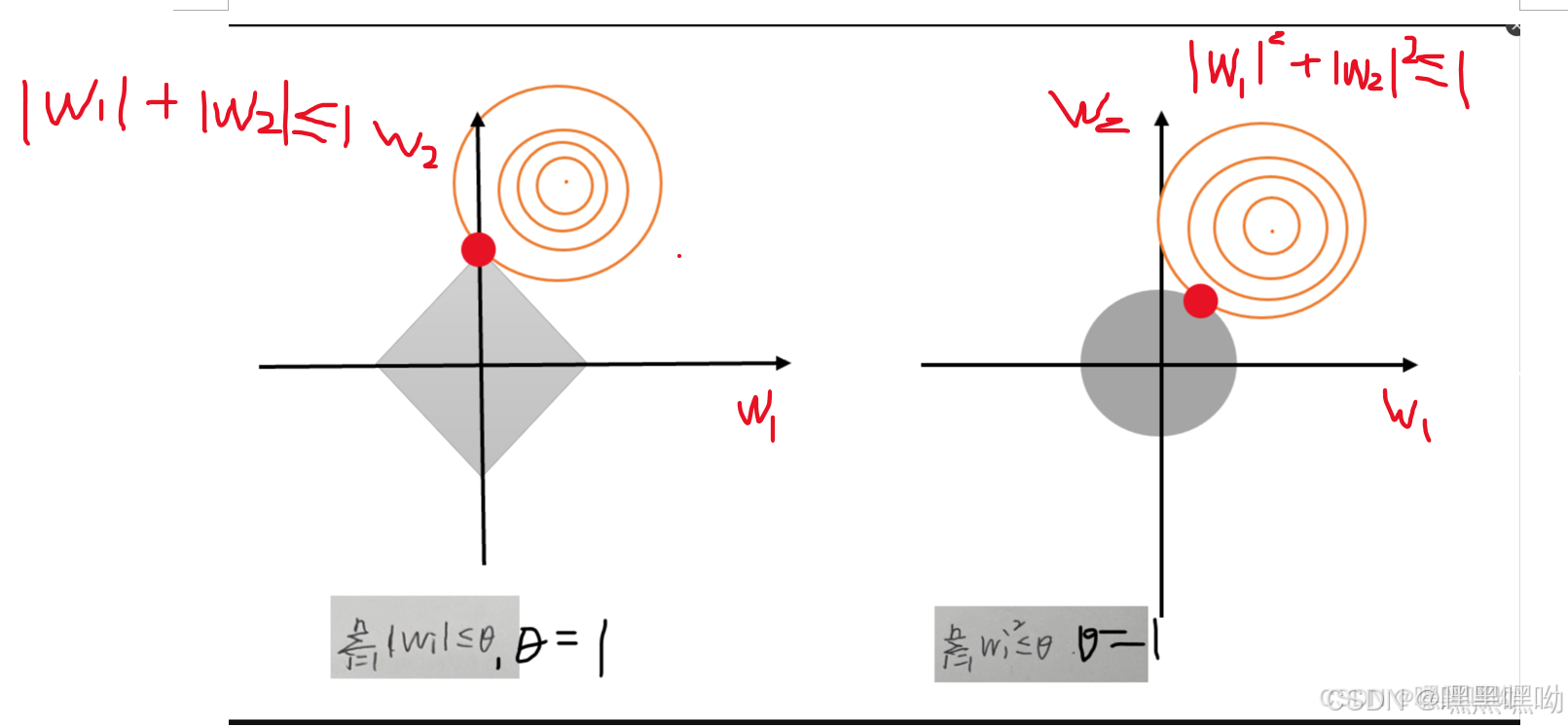
3.Dropout正则化

                                       

在神经网络训练过程中随机丢弃一部分神经元的方法。在每次训练批次中，每个神经元都有一个概率被丢弃。网络的每一层不能依赖于任何一个神经元的输出。

为什么可以解决过拟合？

因为每一层的神经网络对结果影响的权值减小了，而参数又恰恰反映了模型的复杂程度。

5.交叉验证

通过将数据集划分为多个子集，并在不同的子集上训练和验证模型，来评估模型的性能。这种方法确保所有数据都被用于训练和验证，从而提高模型的泛化能力。

1. k 折交叉验证（k-Fold Cross-Validation）：

   • 将数据集划分为 k 个子集（称为“折”）。

   • 每次使用 k-1 个子集作为训练集，剩下的一个子集作为验证集。

   • 重复这个过程 k 次，每次选择不同的子集作为验证集。

   • 最后，计算 k 次验证的平均性能指标。