深度学习 Note.7(线性分类）

1.分类问题概述

线性回归模型：

输出的f是一些连续的值，而我们分类问题输出的值是离散的？那如何拟合呢？

引入非线性决策函数g()

线性分类模型：

可以看到，有了线性判别函数g之后，我们再找一个线性决策边界，也就是图中的直线，我们就可以完成分类。

当判别函数的值大于0是，是在上面；小于0时是在下面

因此：

线性分类模型 = 线性判别函数 + 线性决策边界

分类问题

分类问题可以分为二分类问题和多分类问题。

二分类问题

学习准则（损失函数）

0-1损失函数

将y 与 f 作比较，一样则分类正确，不一样则分类错误。但是不可求导，无法优化

多分类问题

样本量C大于2，一个超平面无法区分

模型

①一对其余：f1区分w1与不是，。。。有较多歧义

②一对一：c*(c-1)/2每两个建立一个。也有歧义，并且当c较大时，分类较多

③argmax: 用投票的方式进行打分，对于模糊的也带入各个函数并归类。没有模糊区域。

                是一对其余的一种改进。（好）

但是对于0-1函数还是没办法进行求导，没法进行学习优化，因此我们要继续学习别的模型。

2.交叉熵与对数似然

信息论中，熵用来衡量一个随机事件的不确定性。 熵越高，随机变量的信息越多，反之则越少。

自信息：一个随机事件所包含的信息量。

一个事情经常发生则没有信息量。

- ? x越大，信息量越少。

log?信息要满足可加性，

从而，熵：随机变量X的自信息的数学期望。

分布越均衡，熵越大。

熵可以用来干什么？

进行熵编码。

对分布p(y)的符号进行编码时 熵H(p)也是理论上最优的平均编码长度，这种编码方式称为熵编码

对于出现次数高的，编码长度小一点。出现次数低的，编码长度大一点。最优

交叉熵(Cross Entropy)
■交叉熵是按照概率分布q的最优编码对真实分布为p的信息进行编码的长度。

在给定q的情况下，如果p和q越接近，交叉熵越小;
                               如果p和q越远，交叉熵就越大.

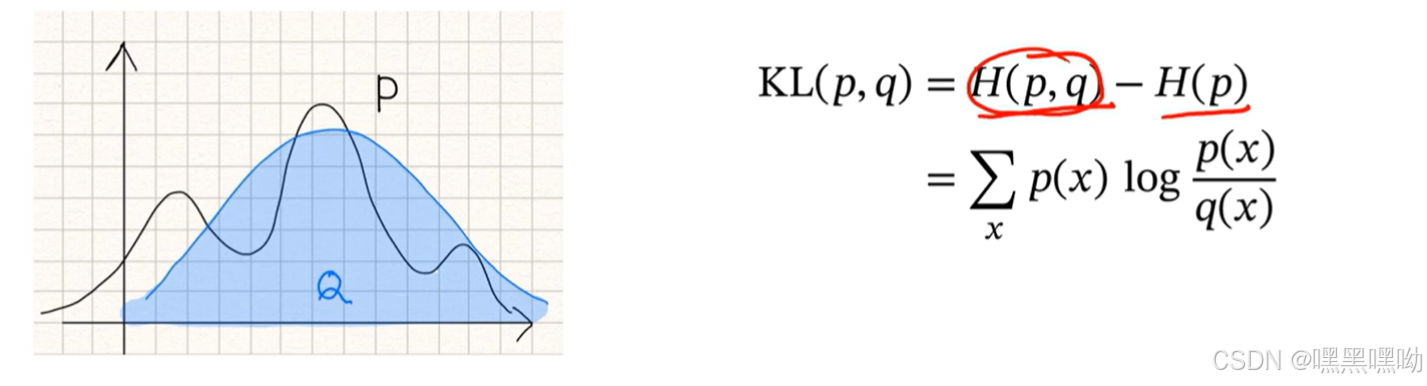
KL散度是用概率分布q来近似p时所造成的信息损失量。
KL散度是按照概率分布q的最优编码对真实分布为p的信息进行编码，其平均编码长度（即交叉熵）H(p,q)和p的最优平均编码长度（即熵）H(p)之间的差异。

应用;

不建立映射，建立概率关系。

   正比于

其实就是最小化两个概率的交叉熵，因为其余取值概率都为0，所以就是取*时的概率，即最大似然。

3.四种线性分类模型

logistic模型

二分类

学习这个模型，确定损失函数。可以看到不可导，无法转化为优化。需要定义一个连续函数

把分类问题转化成概率估计问题

给定x后，y=某个类别的概率

二分类问题只有两种取值，0或1，只用估计1个，剩下用1 减去

logistic函数

sigmoid,两端饱和，连续递增。

logistic回归

 

有了交叉熵，变成一个优化问题，进行学习参数

对上一轮的结果进行改变

y = 1, 更大，更接近于1， y = 0, 更小，更接近于0

没必要优化至交叉熵为0，只需要到两类能够分开即可。