前言
这一系列文章将介绍各种机器学习算法,部分算法涉及公示推导,我的博客中另有板块介绍基于python和R实现各种机器学习算法,详情见置顶的目录。本文介绍支持向量机。我的GitHub上面也会有详细介绍,地址为:https://github.com/roguesir.
算法介绍
支持向量机(Support Vector Machine,SVM),是一种杰出的机器学习算法,在深度神经网络兴起之前,一直成为大规模高级机器学习算法的首选。
SVM与决策树、逻辑回归一样,是一种分类算法,监督学习算法,为了解决传统的线性不可分问题而设计的一种分类算法。
算法推导
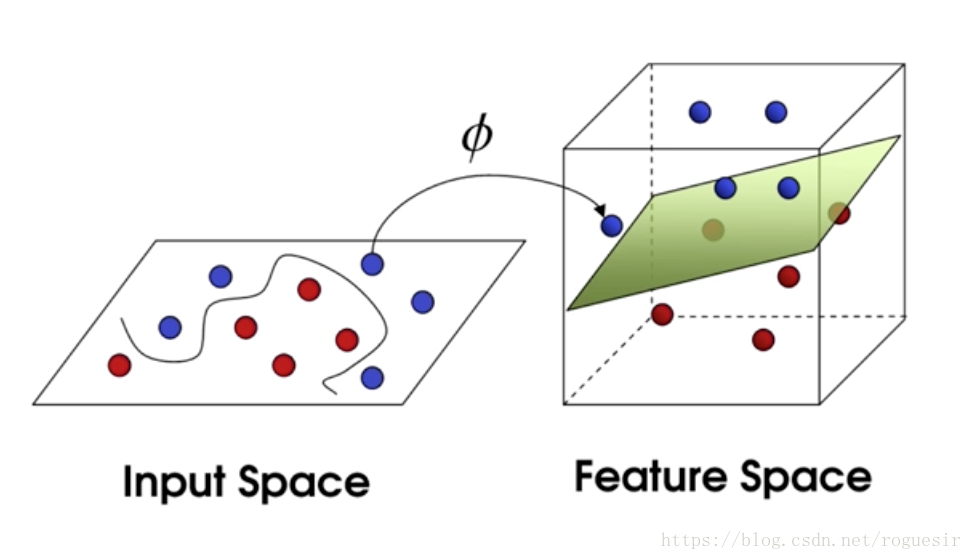
对于一个二分类问题,支持向量机要做的是将多维样本点从input space映射到feature space,这个feature space就是一个超平面,从而将线性不可分问题转化为线性可分问题。
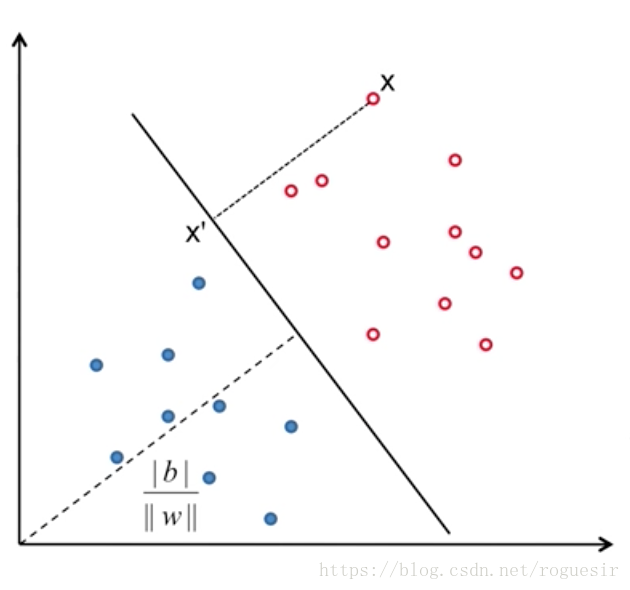
如此,原点到超平面的距离为: (5) d = ∣ b ∣ ∣ ∣ w ∣ ∣ d=\frac{|b|}{||w||} \tag{5} d=∣∣w∣∣∣b∣(5) 空间中会有很多个超平面可以将样本点分开,如何进行选择呢?这里引入了margin这个概念来衡量超平面的好坏。
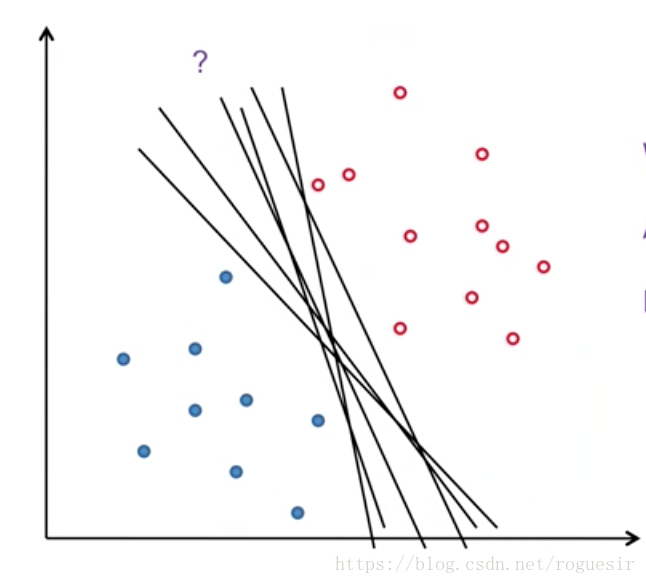










 本文深入探讨了支持向量机(SVM)的基本原理及其解决线性不可分问题的方法。介绍了通过映射样本点到高维空间,使得原本线性不可分的数据变得线性可分,并解释了如何选择最优超平面以最大化正负样本之间的间隔。
本文深入探讨了支持向量机(SVM)的基本原理及其解决线性不可分问题的方法。介绍了通过映射样本点到高维空间,使得原本线性不可分的数据变得线性可分,并解释了如何选择最优超平面以最大化正负样本之间的间隔。
















 367
367

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








