深度学习之五：序列模型与词向量

1 循环序列模型

1.1 序列模型的适用范围

序列模型是一种用于处理序列数据的模型，它可以用于语音识别，音乐生成，情感分类，机器翻译，命名实体识别等。模型的输出也可能是一个序列。

1.2 相关的符号约定

$x^{<k>}$ 表示输入序列中的第k个元素
$y^{<k>}$ 表示输出序列中的第k个元素
$x^{(i)<k>}$ 表示第i个输入序列中的第k个元素
$y^{(i)<k>}$ 表示第i个输出序列中的第k个元素
$T_x$ 表示输入序列的长度
$T_x^{(i)}$ 表示第i个输入序列的长度
$T_y$ 表示输出序列的长度
$T_y^{(i)}$ 表示第i个输出序列的长度

1.3 RNN模型

1.3.1 词的one-hot表示

构造一个词汇表(也称为词典)，若词汇个数为n，词(word)在词典中的位置i记作$w_i$，则词可表示为一个长度为n的一维向量，向量中第$w_i$位置的元素为1，其他位置为0。

1.3.2 模型示意

在处理序列数据时，由于输入和输出长度的不同，且序列模型的维度过高，参数过多，无法使用传统的全联接神经网络来处理，因此必须要使用新的序列化的模型。见下图：

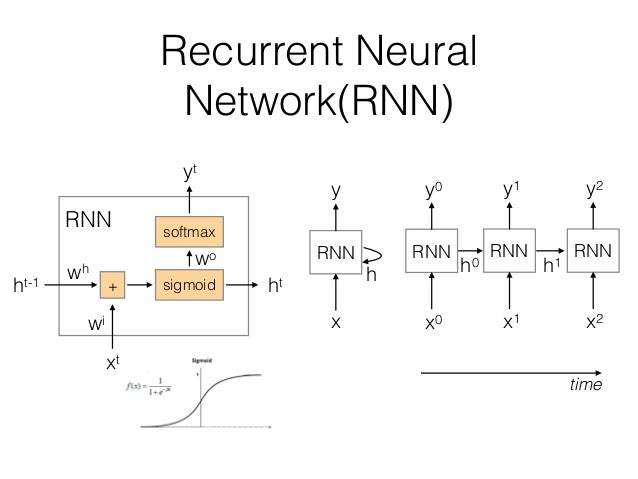
在图中，RNN单元在时刻$t_0$接收输入$x_0$并产生输出$y_0$。在下一个时刻$t_1$，RNN单元同时接收输入$x_1$和上一个时刻的输出$h_0$，从而产生本时刻的输出。这使得RNN可以考虑历史输入的影响。

1.3.3 前向传播

从上图的RNN单元的结构中，可以推导前向传播的计算公式
$h_t = g(W_h*h_{t-1} + W_i x_t + b_h)$
可以将$W_h,W_i$横向堆叠，将$h_{t-1},x_t$纵向堆叠，则公式改写为：
$h_t = g([W_h|W_i]\cdot[\frac{h_{t-1}}{x_t}]+b_h)$
$y_{t} = f(W_o*h_t + b_o)$

1.3.4 RNN前向传播实现

# 实现单个RNN单元内部的计算
def rnn_cell_forward(xt, a_prev, parameters):

    Wax = parameters["Wax"] #alias Wt
    Waa = parameters["Waa"] #alias Wh
    Wya = parameters["Wya"] #alias Wo
    ba = parameters["ba"]   #alias bh
    by = parameters["by"]   #alias bo

    # compute next activation state 
    a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
    yt_pred = softmax(np.dot(Wya, a_next) + by)

    cache = (a_next, a_prev, xt, parameters)
    return a_next, yt_pred, cache

# 实现沿时间序列向前计算
def rnn_forward(x, a0, parameters):
    caches = []

    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape

    # initialize "a" and "y" with zeros
    a = np.zeros((n_a, m, T_x))
    y_pred = np.zeros((n_y, m, T_x))

    a_next = a0

    # loop over all time-steps
    for t in range(T_x):
        # Update next hidden state, compute the prediction, get the cache
        a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)

        a[:,:,t] = a_next
        y_pred[:,:,t] = yt_pred

        caches.append(cache)

    caches = (caches, x)
    return a, y_pred, caches

1.3.4 损失函数

单个样本的损失函数定义为:

L<t>(yˆ<t>,y<t>)=−y