动态规划——编辑距离

最新推荐文章于 2025-06-10 17:50:05 发布

皮蛋瘦肉没有肉

最新推荐文章于 2025-06-10 17:50:05 发布

阅读量586

点赞数

CC 4.0 BY-SA版权

分类专栏：经典算法文章标签：动态规划算法

本文链接：https://blog.youkuaiyun.com/zzp961224/article/details/86494239

经典算法专栏收录该内容

19 篇文章

订阅专栏

本文深入讲解了编辑距离算法，即Levenshtein距离，一种衡量两字符串相似度的方法。通过对比字符串a和b，计算最少操作次数（插入、删除、替换字符）使其相等。文章提供了详细的算法思路和转移方程，并附带C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

参考博客：https://blog.youkuaiyun.com/ghsau/article/details/78903076

题目

编辑距离又称Leveinshtein距离，是由俄罗斯科学家Vladimir Levenshtein在1965年提出。

编辑距离是计算两个文本相似度的算法之一，以字符串为例，字符串a和字符串b的编辑距离是将a转换成b的最小操作次数，这里的操作包括三种：

    插入一个字符
    删除一个字符
    替换一个字符

举个例子，kitten和sitting的编辑距离是3，kitten -> sitten(k替换为s) -> sittin(e替换为i) -> sitting(插入g)，至少要做3次操作。

思路

用lev(i,j)来表示a和b的Leveinshtein距离(i和j分别代表a和b的长度)，则：

当min(i,j)=0时，lev(i,j)=max(i,j)，一个字符串的长度为0，编辑距离自然是另一个字符串的长度
当a[i]=b[j]时，lev(i,j)=lev(i−1,j−1)，比如xxcz和xyz的距离=xxc和xy的距离
否则，lev(i,j)为如下三项的最小值：
1. lev(i−1,j)+1(在a中删除ai)，比如xxc和xyz的距离=xx和xyz的距离+1
2. lev(i,j−1)+1(在a中插入bj)，比如xxc和xyz的距离=xxcz和xyz的距离+1=xxc和xy的距离+1
3. lev(i−1,j−1)+1(在a中把ai替换bj)，比如xxc和xyz的距离=xxz和xyz的距离+1=xx和xy的距离+1

转移方程

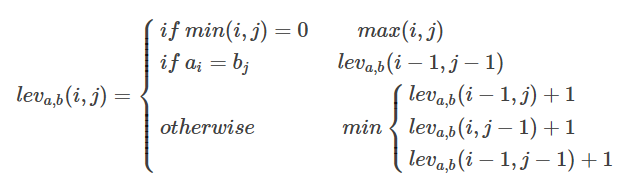
代码：

#include<iostream>
#include<string>
#include<cmath>
using namespace std;
#define maxSize 100
int lev[maxSize][maxSize]={0};
int LEV(string str1,string str2,int len1,int len2)
{
	for(int i=0;i<len1;i++)
	{
		for(int j=0;j<len2;j++)
		{
			if(min(i,j)==0)
				lev[i][j]=max(i,j);
			else if(str1[i-1]==str2[j-1])
			{
				lev[i][j]=lev[i-1][j-1];
			}
			else
			{
				
				int s1=lev[i-1][j]+1;
				int s2=lev[i][j-1]+1;
				int s3=lev[i-1][j-1]+1;
				lev[i][j]=min(s1,min(s2,s3));
			}
		}
	}
	return lev[len1-1][len2-1];
}

int main()
{
	string str1,str2;
	cin>>str1;
	cin>>str2;
	int len1=str1.length();
	int len2=str2.length();
	cout<<LEV(str1,str2,len1,len2)<<endl;
	system("pause");
	return 0;
}