eCommerceGAN : A Generative Adversarial Network for E-commerce
电商网站每年产生的订单只占了所有合理订单的一小部分。然而,探索所有合理订单的空间能更好地理解电子商务系统中不同实体之间的关系,即客户和他们购买的产品。这篇文章的贡献:以密集低维的方式表示订单、ecGAN模型生成订单、ec2GAN模型来生成指定产品的订单
文章目录
1 介绍
低维表示的可行性
产品空间
虽然各大电商网站有数十亿种产品,但是由于产品类别、子类别、价格范围、品牌、制造商等都有内在结构,产品空间的维度其实要低得多。
也就是说在研究产品—顾客关系的时候,必然要把产品表示成向量,但是无需把每个产品都单独地表示出来,也就是说没有必要使用独热向量编码这种方法(不仅高维而且非常稀疏)。从直观上看,要定义一个产品,把它的类别(衣服、电器、美妆等)、价格、制造商等这些表示出来就可以了。不关注单个产品,而是关注由相似产品所组成的产品组,用这个组的整体表示代替单个的产品的表示。
顾客空间
在客户方面,虽然有几亿客户,但客户可以根据购买行为的相似性、价格/品牌敏感度、种族等进行分组,所以他们也能存在于较低维度的空间。
订单空间
理论上,在把产品映射到一个低维的产品空间、顾客映射到一个低维的顾客空间之后,整个电子商务订单是这两个空间的点的笛卡尔积(原文是interaction
,但我觉得用笛卡尔积的概念更容易理解)。但是其中,某些点是合理的,某些点是不合理的。也就是说,有些顾客就不会买某些产品(比如在不考虑买礼物、代购等特殊情况下,一个老人就不会买奶嘴之类的东西)。
但是已经在电子商务网站上产生的订单只占所有可信订单的一小部分。探索合理订单的空间可以为产品需求、客户偏好、价格估计、季节变化等提供重要的见解,可能会直接或间接影响收入和客户满意度。
论文主要内容
这篇文章的主要内容:
- 订单的四元组表示法:
{customer,product,price,date}。每个分量都是稠密低维的向量 - ecGAN生成订单。
- ec2GAN包含特定产品的订单。
2 预备知识
GAN
组成:生成器(G)和判别器(D)
| Input | Output | |
|---|---|---|
| 生成器G | 随机噪声向量 | 与真实数据点相似的样本 |
| 判别器D | 样本点 | 真或假程度([0~1]) |
随机噪声的含义
随机噪声是一个符合高斯分布的随机变量,GAN本来就是完成一个分布的变换,GAN的生成器就是把一个高斯分布(或其他随机分布)变换成目标数据分布。这里实际是把输入的随机变量当成了数据的latent space。以生成人脸为例,人脸有不同的姿态、人种、年龄、表情、发型、肤色、妆容等,可以理解为多个分布的组合。
符号定义
p
D
a
t
a
(
x
)
:
真
实
数
据
分
布
p
Z
(
z
)
:
噪
声
分
布
,
(
采
用
标
准
正
态
分
布
)
D
:
X
→
[
0
,
1
]
G
:
Z
→
X
′
p_{Data}(x):真实数据分布\\ p_Z(z):噪声分布,(采用标准正态分布) \\ D:X \rightarrow [0, 1] \\ G:Z \rightarrow X'
pData(x):真实数据分布pZ(z):噪声分布,(采用标准正态分布)D:X→[0,1]G:Z→X′
最大最小博弈
- 对判别器D来讲,目的是输入真实数据尽量输出1,输入虚假数据尽量输出0。
- 对生成器G来讲,目的是产生的数据输入到D后,尽量输出1。
所以D和G之间的博弈关系可以表示成:
m
a
x
D
m
i
n
G
V
(
D
,
G
)
=
E
x
∼
P
D
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
+
E
z
∼
P
Z
(
z
)
[
1
−
l
o
g
(
D
(
G
(
z
)
)
)
]
max_D \space min_G V(D,G) = E_{x∼P_{Data(x)}}[logD(x)] + E_{z∼P_{Z(z)}}[1-log(D(G(z)))]
maxD minGV(D,G)=Ex∼PData(x)[logD(x)]+Ez∼PZ(z)[1−log(D(G(z)))]
得到的优化代价函数:
J
(
D
)
=
−
1
2
E
x
∼
P
D
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
−
1
2
E
z
∼
P
Z
(
z
)
[
1
−
l
o
g
(
D
(
G
(
z
)
)
)
]
J
(
G
)
=
−
J
(
D
)
通
常
用
:
J
(
G
)
=
−
l
o
g
(
D
(
G
(
z
)
)
)
J^{(D)} = - \frac{1}{2}E_{x∼P_{Data(x)}}[logD(x)] -\frac{1}{2} E_{z∼P_{Z(z)}}[1-log(D(G(z)))] \\ J^{(G)} = - J^{(D)} 通常用:J^{(G)} = -log(D(G(z)))
J(D)=−21Ex∼PData(x)[logD(x)]−21Ez∼PZ(z)[1−log(D(G(z)))]J(G)=−J(D)通常用:J(G)=−log(D(G(z)))
WGAN
最初的GAN论文使用最小化JS散度,但是使用JS散度必须保证处处连续可微所以很难。大部分GAN的变体都是使用最小化f-散度来学习真实数据的分布。有人提出了
Earth Mover's distance(Wasserstein距离,又称EM距离)作为一种更好的替代方案。下文主要讨论WGAN(Wasserstein距离)
符号:
P
r
:
真
实
数
据
分
布
P
g
:
真
实
数
据
的
近
似
分
布
θ
:
要
学
习
的
参
数
g
θ
(
z
)
=
P
g
P_r:真实数据分布\\ P_g:真实数据的近似分布 \\ θ:要学习的参数 \\ g_θ(z) = P_g \\
Pr:真实数据分布Pg:真实数据的近似分布θ:要学习的参数gθ(z)=Pg
生成器G的目标是其产生的数据分布和真实数据分布尽可能接近,根据Wasserstein距离的公式有:
W ( P r , P g ) = i n f γ ∈ ∏ ( P r , P g ) E ( x , y ) ∈ γ [ ∣ ∣ x − y ∣ ∣ ] W(P_r,P_g) = inf_{γ∈∏(P_r,P_g)} E_{(x,y)∈γ}[||x-y||]\\ W(Pr,Pg)=infγ∈∏(Pr,Pg)E(x,y)∈γ[∣∣x−y∣∣]
解释: ( P r , P g ) (P_r,P_g) (Pr,Pg)是 P r P_r Pr和 P g P_g Pg分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布 γ γ γ,可以从中采样 ( x , y ) ∼ γ (x,y)\sim γ (x,y)∼γ得到哟个样本x和y并计算出这对样本的距离 ∣ ∣ ∣ x − y ∣ |||x-y| ∣∣∣x−y∣,所以可以计算该联合分布下,样本对距离的期望 E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] E(x, y)\sim \gamma[||x-y||] E(x,y)∼γ[∣∣x−y∣∣]。在所有可能的联合分布中能够对这个期望取到的下界 i n f γ ∈ ∏ ( P r , P g ) E ( x , y ) ∈ γ [ ∣ ∣ x − y ∣ ∣ ] inf_{γ∈∏(P_r,P_g)} E_{(x,y)∈γ}[||x-y||] infγ∈∏(Pr,Pg)E(x,y)∈γ[∣∣x−y∣∣]就是Wasserstein距离。
但是直接使用上述公式计算Wasserstein距离很难,根据Kantorovich-Rubinstein对偶原理可以得到以下等式:
W ( P r , P g ) = s u p ∣ ∣ f ∣ ∣ L ≤ 1 E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] W(P_r,P_g) = sup_{||f||_{L}≤1} E_{x∼P_r}[f(x)] - E_{x∼P_g}[f(x)]\\ W(Pr,Pg)=sup∣∣f∣∣L≤1Ex∼Pr[f(x)]−Ex∼Pg[f(x)]
最终更新公式如下:
▽
θ
W
(
P
r
,
P
g
)
=
▽
θ
(
E
x
∼
P
r
[
f
w
(
x
)
]
−
E
z
∼
P
Z
(
z
)
[
f
w
(
g
θ
(
z
)
)
]
)
▽_{θ}W(P_r,P_g) = ▽_{θ}(E_{x∼P_r}[f_w(x)] - E_{z∼P_Z(z)}[f_w(g_θ(z))])\\
▽θW(Pr,Pg)=▽θ(Ex∼Pr[fw(x)]−Ez∼PZ(z)[fw(gθ(z))])
这里的$f_w$是Wasserstein距离的最优利普西兹函数连续函数。
WGAN步骤:
- 固定
θ,通过训练$f_w$计算Wasserstein距离距离直至收敛。 - 计算θ的梯度:
− E z ∼ P Z ( z ) [ ▽ θ f w ( g θ ( z ) ) ] -E_{z∼P_Z(z)}[▽_{θ}f_w(g_θ(z))] −Ez∼PZ(z)[▽θfw(gθ(z))] - 更新θ
J W ( D ) = − E x ∼ P g [ D ( x ) ] + E x ∼ P r [ D ( x ) ] − λ E x ∼ P x ′ [ ∣ ∣ ▽ x D ( x ) ∣ ∣ 2 − 1 ] 2 J W ( G ) = − J W ( D ) J_W^{(D)} = -E_{x∼P_{g}}[D(x)] + E_{x∼P_{r}}[D(x)] - λ E_{x∼P_{x'}}[||▽_{x}D(x)||_2-1]^2\\ J_W^{(G)} = - J_W^{(D)} JW(D)=−Ex∼Pg[D(x)]+Ex∼Pr[D(x)]−λEx∼Px′[∣∣▽xD(x)∣∣2−1]2JW(G)=−JW(D)
3 订单表示
订单的四元组表示法:{产品,人,价格,时间}
产品表示
产品标题中的所有单词加权平均的word2vec表示来创建低维产品向量
- 训练一个word2vec模型(原文:随机选择1.43亿个产品的标题和描述作为语料库,得到了140万左右的词汇量及其word2vec表示)
- 计算逆向文档频率(IDF)
- 每个产品的标题的单词的word2vec表示根据IDF加权平均,再根据总IDF值规范化。
使用这种方法创建的嵌入表示是128维的,值的范围在-1和1之间。
顾客表示
为表示顾客,使用一个判别式多任务循环神经网络(如下图),RNN中客户最近购买历史相关的不同信号被显式编码到其嵌入表示中。
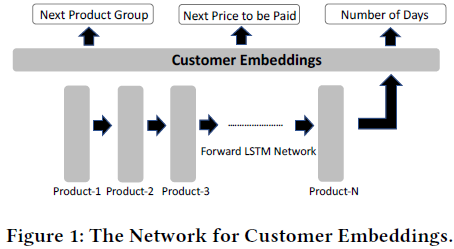
使用的三种不同的训练任务:
- 顾客下一个购买的产品的类别(如衣服、食品、家具、婴儿产品等)
- 顾客下一个购买的价格
- 顾客下一个购买的时间差(以天为单位)
网络结构:
- 输入:产品序列,每个产品的表示是之前提到的128维向量
- 隐藏层:128维的顾客表示
- 输出:每次迭代,随机选择任务之一进行优化,采取交替优化的方式
使用此方法创建的嵌入是128维的,值的范围在-1和1之间。
价格
先取对数后正则化,值的范围在-1和1之间
购买日期
7维向量编码
| 维度 | 含义 |
|---|---|
| 1 | 当前日期和预先确定的纪元之间的差值 |
| 2和3 | 月的哪一天 |
| 4和5 | 周的哪一天 |
| 6和7 | 哪个月 |
通过在一个单位圆的外围投影可能的日/月,并使用它们的正弦和余弦分量来表示。
每个分量在-1和1之间。
订单表示
264维的向量
- 128维产品表示
- 128维顾客表示
- 1维的价格
- 7维的时间
4 网络结构
ecGAN
使用WGAN为订单空间建模。
生成器:
全连接网络,具有两个隐藏层,每一隐藏层的末端具有ReLU非线性变换。
它将噪声矢量映射到可行的订单空间。
判别器:
全连接网络,具有两个隐藏层,每一隐藏层的末端具有ReLU非线性变换。
将生成器产生的订单与真实订单区别开来。(识别真假)
参数
- 生成器:96——64——128——264
- 判别器:264——128——64——1
ec2GAN
生成包含特定产品的订单
ec2GAN是在ecGAN的基础上进行修改而获得的。
- 输入方面:ecGAN的输入仅有噪声向量,ec2GAN的输入是噪声向量拼接上具体的128维产品嵌入
- 损失函数方面:
J ( R ) = ∣ ∣ P j − P j ∼ ∣ ∣ α J W ( G ) + ( 1 − α ) J ( R ) J^{(R)} = ||P_j-P^{\sim}_j||\\ \alpha J^{(G)}_W+(1-\alpha)J^{(R)} J(R)=∣∣Pj−Pj∼∣∣αJW(G)+(1−α)J(R) - 网络结构:与ecGAN相同
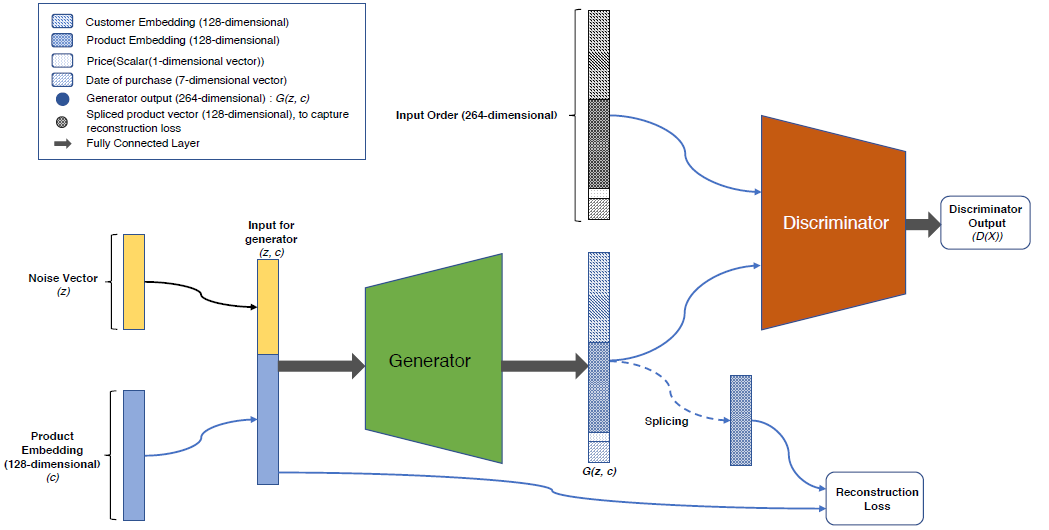
参数
- 生成器:96+128=224——64——128——264
- 判别器:264——128——64——1





















 2078
2078

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








