Leetcode 鸡蛋掉落 的改进思路

Leetcode 鸡蛋掉落 的改进思路

在这位dalao的基础上做出改进

https://www.cnblogs.com/yunlambert/p/10028865.html

原题与异常情况

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。
你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

尤其注意：
示例 3：

输入：K = 3, N = 14
输出：4

在理解完大佬的思路后，论证示例三的k=3,n=14时出现了差错！

下文以偏心树来表示dalao的树

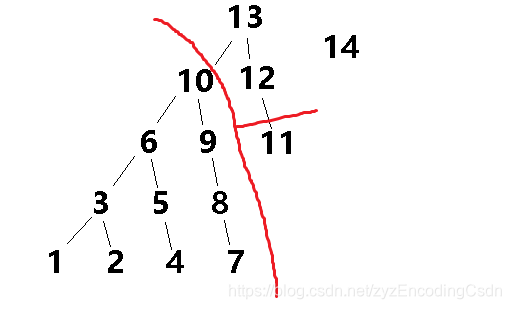
前十个数是可以通过大佬的方法得出结果的，第11个数与前10个数是对立关系(非1~10即为11)，也是可以得出结果的，然而当F为12,13,14时，大佬的方法就行不通了。

改进思路

在我烦恼的同时，我发现了示例3的条件是k=3而不是k=2,这表明鸡蛋的个数也可以影响输出结果，所以应该存在一种普适性较强的算法使得楼层和鸡蛋都与F相关。

算法原理与注意事项

二节点等于鸡蛋的损失点，或二节点有鸡蛋损失的风险，这在所有树形结构中通用。

二节点代表从此节点数的楼层扔出的鸡蛋有被摔碎的可能，这种鸡蛋的牺牲对问题的解是毫无价值的(??)，反而偏心树中单节点的鸡蛋的碎裂代表着问题的解，代表得出F的值。

具体思路

在看大佬们的博客之前，我傻乎乎的用着二分法来确定F值，当然这是不行的，原因如下：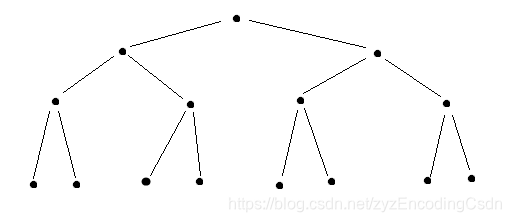
二叉树的缺点在于二节点过多，意味着鸡蛋的牺牲，二叉树模式运行的代价是对鸡蛋的极大浪费，这表示当你手里的鸡蛋全碎时，还有部分子树没有遍历。

但是二叉树并非一无是处，二叉树可以帮助我们折半缩小查询范围，它可以把鸡蛋做为代价实现对数据的指数式缩减（y=2的鸡蛋个数的次方），相较于偏心树的等差缩减的效率高得多。

实现方式

当鸡蛋多于两个(偏心树的运行的充要条件是至少有两个鸡蛋)时，我们应该先用二分查找法贪心，贪婪的把鸡蛋献祭到2个为止，实现鸡蛋的最高价值利用，在范围缩减后的基础上继续使用偏心树来求得问题的准确解。

java伪代码：

		//判别鸡蛋个数，准备预处理
		if(k-2>0){
			System.out.println("以鸡蛋的牺牲为代价对N使用二分法缩小查询范围，当剩余鸡蛋为两个时停止鸡蛋的牺牲");
		}else if(k==1){
			System.out.println("单鸡蛋的情况略");
		}
		//执行稳定的偏心树操作
		System.out.println("对当前的N与活下来的两个鸡蛋进行偏心树操作，得出准确解");

PS与感悟

这种以鸡蛋换范围(二分法)的方法类似扫雷游戏的开局瞎XX点，有可能点出一块空地也有可能踩雷，稳定的进行扫雷游戏还是得按规矩(偏心树)来，当然，扫雷游戏里的鸡蛋(机会)只有一个(次)，还是遵守规则的好。
本人并非科班出身，对大部分概念无法做到术语覆盖，只能以浅显易懂的语言解释原理与思想，这也是本人第一次写csdn，有些标签与格式段落还不太熟悉，希望大家包涵了。